ഭാരതീയഗണിതശാസ്ത്രത്തിലെ പല സിദ്ധാന്തങ്ങള്ക്കു് ആധുനികഗണിതത്തിലെ സിദ്ധാന്തങ്ങളുമായുള്ള ബന്ധം ഒറ്റ നോട്ടത്തില് പ്രകടമാകാത്തതു് സങ്കേതത്തി(notation)ലുള്ള വ്യത്യാസം മൂലമാണു്. ഇനി പ്രതിപാദിക്കാന് പോകുന്ന, ജ്യാമിതി(Geometry)യെപ്പറ്റിയുള്ള ചില ലേഖനങ്ങള് മനസ്സിലാക്കാന് ഉപകരിക്കുന്ന ചില സങ്കേതങ്ങള് താഴെച്ചേര്ക്കുന്നു.
ആധുനികഗണിതം sin x, cos x തുടങ്ങിയ ത്രികോണമിതിയിലുള്ള സങ്കേതങ്ങള് ഉപയോഗിക്കുന്നിടത്തു് ഭാരതീയര് ഭുജ, കോടി, ജ്യാ, കര്ണ്ണം എന്നിവ ഉപയോഗിച്ചിരുന്നു.
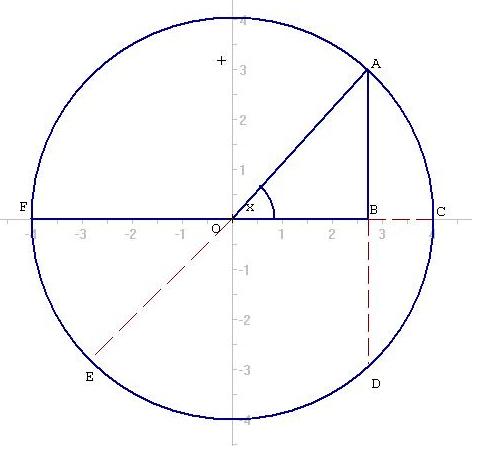
ചിത്രത്തില് OAB ഒരു മട്ടത്രികോണം (Right-angled triangle) ആണു്. B ആണു് മട്ടകോണ് (right angle). x എന്ന കോണിനെ വ്യവഹരിക്കുമ്പോള് OB എന്ന വശത്തെ ഭുജം (adjacent side) എന്നും AB എന്ന വശത്തെ ജ്യാ (opposite side) എന്നും വിളിക്കുന്നു. OA-യെ കര്ണ്ണം (hypotenuse) എന്നാണു വിളിക്കുന്നതു്. ഭുജമ്, ജ്യാ എന്നിവയിലൊന്നു് ഉപയോഗിക്കുമ്പോള് മറ്റേതിനെ കോടി (“കോടീ” എന്നു സംസ്കൃതത്തില്. നൂറു ലക്ഷം എന്ന സംഖ്യ “കോടി” ആണു്.) എന്നും പറയാറുണ്ടു്. അതായതു്, കോടി എന്നതു് ഭുജമോ ജ്യാവോ ആകാമെന്നര്ത്ഥം.
ത്രികോണത്തെ പരിഗണിക്കുമ്പോള്,
കര്ണ്ണം = OA = r
ഭുജം = OB = OA cos x = r cos x
ജ്യാ = AB = OA sin x = r sinx
കോടി എന്നതു ഭുജമോ ജ്യാവോ ആകാം.
കര്ണ്ണം വ്യാസാര്ദ്ധമായുള്ള വൃത്തത്തെ ഇതിനോടൊപ്പം പരിഗണിക്കാറുണ്ടു്. ഇവിടെ ACDയെ ചാപം (വില്ലു്) എന്നും ABDയെ ജ്യാ (ഞാണ്) എന്നും (ഈ ജ്യാ മുമ്പു പറഞ്ഞ ജ്യാവിന്റെ ഇരട്ടിയാണു്) BCയെ ശരം എന്നും വിളിക്കുന്നു.
വൃത്തത്തെ പരിഗണിക്കുമ്പോള്,
വൃത്തത്തിന്റെ വ്യാസാര്ദ്ധം = OA = r
ജ്യാ = AD = 2 AB = 2r sin x
ശരം = BC = r – r cos x
ചാപം = ACD = rx (x റേഡിയനില്)
ഇവയുടെ പര്യായങ്ങളും ഉപയോഗിക്കാറുണ്ടു്. ഭുജം എന്നതിനു പകരം ബാഹു, പാണി തുടങ്ങിയവയും, ചാപത്തിനു പകരം ധനു തുടങ്ങിയവയും.

Post a Comment