Gurukulam | ഗുരുകുലം

ആധുനികഭാരതത്തിലെ ഏറ്റവും മഹാനായ ഗണിതശാസ്ത്രജ്ഞനായിരുന്നു ശ്രീനിവാസരാമാനുജന്‍. നമ്മുടെ അശാസ്ത്രീയമായ വിദ്യാഭ്യാസസമ്പ്രദായത്തിന്റെ ബലിയാടായി പരീക്ഷകളില്‍ തോല്‍ക്കുകയും ക്ലാസ്സുകയറ്റം നിഷേധിക്കപ്പെടുകയും ചെയ്തു്, പില്‍ക്കാലത്തു ലോകത്തെമ്പാടുമുള്ള ഗണിതശാസ്ത്രജ്ഞരെ അമ്പരപ്പിച്ച (ഇന്നും അമ്പരപ്പിച്ചുകൊണ്ടിരിക്കുന്ന) സിദ്ധാന്തങ്ങള്‍ തന്റെ പഴയ വീട്ടിലെ ബെഞ്ചിലിരുന്നു് തന്റെ നോട്ടുബുക്കുകളില്‍ കുറിച്ചിട്ട അസാമാന്യപ്രതിഭാശാലി. ജി. എച്ച്. ഹാര്‍ഡി കണ്ടെത്തിയിരുന്നില്ലെങ്കില്‍ ഇന്നും ഈ “കാന്തിയും മൂല്യവും വാച്ചിടും” രത്നം “ചാണ കാണാതെ” ഭാരതാംബയുടെ കുക്ഷിയില്‍ മറഞ്ഞുപോയേനേ.

രാമാനുജനെപ്പറ്റിയുള്ള കഥകള്‍ പലപ്പോഴും അതിഭാവുകത്വത്തിലേക്കു കടക്കാറുണ്ടു്. പലപ്പോഴും അദ്ദേഹത്തിന്റെ ഗണിതശാസ്ത്രജ്ഞാനത്തെയും കഴിവിനെയും സത്യസന്ധമായി വിശകലനം ചെയ്യുന്നതിനു പകരം, അദ്ദേഹത്തെ ഒരു അമാനുഷനാക്കുന്ന കഥകളാണു നാം കേള്‍ക്കുന്നതു്.

ഇതിനു് ഒരു നല്ല ഉദാഹരണമാണു് രാമാനുജനും 1729 എന്ന സംഖ്യയും ഉള്‍പ്പെടുന്ന ഈ സംഭവം. ഹാര്‍ഡി പറയുന്നു:

I remember once going to see him when he was ill at Putney. I had ridden in taxi cab number 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavurable omen. “No,” he replied, “it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways.”

അതായതു്, രോഗശയ്യയിലായിരുന്ന രാമാനുജനോടു് ഹാര്‍ഡി 1729 (ഹാര്‍ഡി സഞ്ചരിച്ച ടാക്സിയുടെ നമ്പര്‍) ഒരു ചീത്ത സംഖ്യയാണു് എന്നു പറഞ്ഞപ്പോള്‍, അതു് രണ്ടു ഘനസംഖ്യകളുടെ തുകയായി രണ്ടു വിധത്തിലെഴുതാവുന്ന ഏറ്റവും ചെറിയ സംഖ്യയാണെന്നു് രാമാനുജന്‍ ഉത്തരം പറഞ്ഞു.

ഇത്രയും നടന്ന കാര്യം. (യുക്തിവാദിയായിരുന്ന ഹാര്‍ഡി unfavourable omen എന്നു പറഞ്ഞതു് വിശ്വാസിയായ രാമാനുജനോടായതുകൊണ്ടാവാം.) ഇതില്‍നിന്നു വീരഗാഥയെഴുതുന്ന പാണന്മാര്‍ കണ്ടെത്തുന്നതു് ഏതു സംഖ്യ കിട്ടിയാലും ഞൊടിയിടയ്ക്കുള്ളില്‍ അതിന്റെ ഇത്രയും ദുര്‍ഗ്രഹമായ പ്രത്യേകതകള്‍ കണ്ടുപിടിക്കാന്‍ പറ്റുന്ന അസാമാന്യപ്രതിഭ എന്നാണു്.

സത്യത്തില്‍ രാമാനുജനു് 1729-ന്റെ ഈ പ്രത്യേകത നേരത്തേ അറിയാമായിരുന്നു. രാമാനുജന്റെ അവസാനത്തെ നോട്ടുബുക്ക് എവിടെയോ വെച്ചു നഷ്ടമായതു് അദ്ദേഹം മരിച്ചു വളരെക്കാലം കഴിഞ്ഞാണു് (1965-ല്‍) കണ്ടെടുക്കുന്നതു്. ഇതിലെ സിദ്ധാന്തങ്ങള്‍ ഇന്നും ദുര്‍ഗ്രഹങ്ങളായി നിലകൊള്ളുന്നു. 1987-ല്‍ Tata Institute of Fundamental Research-ഉം Narosa Publishers-ഉം ചേര്‍ന്നു് രാമാനുജന്റെ നഷ്ടപ്പെട്ട കുറിപ്പുകള്‍ (Lost Notebook) ഫോട്ടോസ്റ്റാറ്റ് രൂപത്തില്‍ പ്രസിദ്ധീകരിച്ചു. അതിന്റെ 341-ാ‍ം പേജില്‍ ഇങ്ങനെ കാണാം:

If

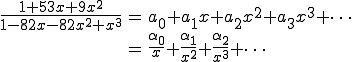
then

Examples:

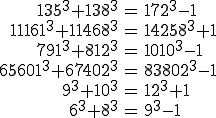
അവസാനത്തേതിനു തൊട്ടുമുമ്പിലുള്ള ഉദാഹരണം ശ്രദ്ധിക്കൂ. 1729 ആണു് അതിന്റെ മൂല്യം. ഈ സിദ്ധാന്തത്തെപ്പറ്റി പഠിച്ച സമയത്തു് 1729-ന്റെ ഈ പ്രത്യേകത രാമാനുജന്‍ ശ്രദ്ധിച്ചിട്ടുണ്ടാവണം. അതു് ആ സന്ദര്‍ഭത്തില്‍ പറഞ്ഞിട്ടുമുണ്ടാവണം. രോഗശയ്യയായിരുന്നതിനാല്‍ സംസാരവിഷയം പെട്ടെന്നു മാറിപ്പോയിട്ടുണ്ടാവണം. രാമാനുജന്റെ മരണത്തിനു ശേഷമായിരിക്കണം ഹാര്‍ഡി ഇതു പിന്നെ ഓര്‍ത്തതും രേഖപ്പെടുത്തിയതും. ഹാര്‍ഡിക്കോ പിന്നെ ചരിത്രം രേഖപ്പെടുത്തിയവര്‍ക്കോ രാമാനുജനെഴുതിയ ഈ കുറിപ്പുകളെപ്പറ്റി അറിവുണ്ടായിരുന്നില്ല. 1987-നു ശേഷവും ആരെങ്കിലും ഇതു ശ്രദ്ധിച്ചതായി എനിക്കറിവില്ല.

ഇനി, ഈ സിദ്ധാന്തം ശ്രദ്ധിക്കൂ. ഇതെങ്ങനെ കിട്ടിയെന്നോ, ഇതെങ്ങനെ തെളിയിക്കുമെന്നോ, ഇതില്‍ നിന്നു് മേല്‍പ്പറഞ്ഞ ഉദാഹരണങ്ങള്‍ എങ്ങനെ ഉണ്ടാക്കിയെടുക്കുമെന്നോ എനിക്കു വലിയ പിടിയില്ല. അവിടെയാണു് ഗവേഷണം ആവശ്യമാവുന്നതു്. അവിടെയാണു് രാമാനുജന്റെ പ്രതിഭ കുടികൊള്ളുന്നതു്. ഒരു അജ്ഞാതസംഖ്യയെപ്പറ്റി ഞൊടിയിടയ്ക്കുള്ളില്‍ ഒരു സിദ്ധാന്തം “ഉണ്ടാക്കിയെടുത്തതില്‍” അല്ല.