മുന്പേ നടന്ന ഗുരുക്കള് തെളിച്ച ദീപപ്രകാശത്തില് ലോകത്തെ കാണാനൊരു ശ്രമം…
(To follow this blog, scroll to the bottom of this page. To subscribe posts by email, click here.)
{ Category Archives }
കലിദിനസംഖ്യയെപ്പറ്റി ഇതുവരെ എഴുതാന്‍ കഴിഞ്ഞില്ല. താമസിയാതെ എഴുതാം.
ഏതു ദിവസത്തിന്റെയും കലിദിനസംഖ്യ കണ്ടുപിടിക്കാനും, കലിദിനസംഖ്യയില്‍ നിന്നു തീയതി കണ്ടുപിടിക്കാനുമുള്ള ഒരു ഓണ്‍‌ലൈന്‍ പ്രോഗ്രാം ഇവിടെ ഇട്ടിട്ടുണ്ടു്. ഇംഗ്ലീഷില്‍ ഒരു ചെറിയ കുറിപ്പും ഇട്ടിട്ടുണ്ടു്. ദയവായി പരീക്ഷിച്ചുനോക്കുക. അഭിപ്രായങ്ങള്‍ അറിയിക്കുക.
മനോരമയും മാതൃഭൂമിയും എന്തു വേണമെങ്കിലും പറയട്ടേ. നമുക്കു് വിഷു ആഘോഷിക്കാം.
എല്ലാവര്‍ക്കും വിഷു ആശംസകള്‍.
വിഷുക്കണിക്കാവശ്യമായ എല്ലാ സാമഗ്രികളും കിട്ടാത്തതുകൊണ്ടു് കണിയുടെ പടം പോസ്റ്റുചെയ്യുന്നില്ല.
കാലമിനിയുമുരുളും, വിഷു വരും, വര്‍ഷം വരും, തിരുവാതിര വരും…
അന്നൊക്കെ ആരെന്നുമെന്തെന്നും,
ആര്‍ക്കൊക്കെ ബ്ലോഗറു ബ്ലോക്കെന്നും,
ആര്‍ക്കൊക്കെ ബ്ലോഗിനു കോപ്പൊക്കെ തീര്‍ന്നെന്നും,
ജോലി കുമിഞ്ഞെന്നും,
സമയം കുറഞ്ഞെന്നും,
പ്രാരബ്ധമായെന്നും,
സ്വാതന്ത്ര്യം പോയെന്നും,
ബ്ലോഗുറവ വറ്റീന്നും,
നാട്ടീന്നു പോണെന്നും,
കമ്പ്യൂട്ടര്‍ ചത്തെന്നും,
ഭാഷ മറന്നെന്നും,
വരമൊഴി മറന്നെന്നും,
ആല്‍‌ഷെമിഴ്സ് ബാധിച്ചു മൊത്തം മറന്നെന്നും,
കൈവിരല്‍ വിറച്ചെന്നും,
വിറ വിട്ട കൈകള്‍ക്കു കൂച്ചുവിലങ്ങെന്നും,
കണ്ണുകളടഞ്ഞെന്നും,
അടയാത്ത കണ്‍കളില്‍ തിമിരം പിടിച്ചെന്നും,
പതറുന്നു വാക്കെന്നും,
പതറാത്ത വാക്കുകളില്‍ ഗര്‍വ്വം കലര്‍ന്നെന്നും,
അരുതാത്ത ചെയ്തികളില്‍ ജീവിതമലഞ്ഞെന്നും,
അലറുന്ന കാലത്തൊടെതിരേറ്റു തോറ്റെന്നും,
അറിയുന്നതാരുണ്ടു്?
അതിനാല്‍,
വരിക സഖാക്കളേ,
അരികത്തു ചേര്‍ന്നു നില്‍ക്കൂ…
ഒരുമിച്ചു കൈകള്‍ കോര്‍ത്തെതിരേറ്റിടാം നമുക്കിന്നത്തെ വിഷുവിനെ,
എന്നിട്ടു നമ്മള്‍ക്കു
കുശുകുശുപ്പില്ലാത്ത,
കുന്നായ്മയില്ലാത്ത,
പരിഹാസമുതിരാത്ത,
സഹജരെക്കുത്താത്ത,
സഹനവും സമതയും കൈയില്‍ മുതലായുള്ള
പുതിയൊരു ബൂലോകമുണ്ടാക്കിടാം, അതില്‍
പുതിയൊരു സൌഹാര്‍ദ്ദമേകാം, പരസ്പരം
ഊന്നുവടികളായ് നില്‍ക്കാം….
(കക്കാടിനോടും അയ്യപ്പപ്പണിക്കരോടും കടപ്പാടു്)
കിടന്നിട്ടു് ഉറക്കം ശരിയായില്ല. മാതൃഭൂമി പഞ്ചാംഗത്തിനു് ഇങ്ങനെയൊരു തെറ്റു വരാന്‍ എന്താണു കാരണം എന്ന ഒരു കണ്‍ഫ്യൂഷന്‍.
ഇന്നലെ നാട്ടില്‍ നിന്നു മടങ്ങി വന്ന ഒരു സുഹൃത്തു് ഇക്കൊല്ലത്തെ ഒരു മാതൃഭൂമി കലണ്ടര്‍ കൊണ്ടു തന്നിരുന്നു. അതിലെ സംക്രമങ്ങളൊക്കെ പരിശോധിച്ചപ്പോള്‍ ഒരു കാര്യം വ്യക്തമായി – എല്ലാ സംക്രമങ്ങള്‍ക്കും ഏകദേശം 33 മിനിട്ടിന്റെ വ്യത്യാസമുണ്ടു്.
ഇക്കൊല്ലത്തെ സംക്രമങ്ങളുടെ സമയങ്ങള്‍ താഴെച്ചേര്‍ക്കുന്നു:
| മലയാളമാസം | സംക്രമം | സംക്രമസമയം | സംക്രമസമയം |
| (തീയതി) | (ഞാന്‍) | (മാതൃഭൂമി) | |
| മകരം | 2006/01/14 | 11:53 A | 11:26 A |
| കുംഭം | 2006/02/13 | 12:53 A | 12:21 A |
| മീനം | 2006/03/14 | 09:45 P | 09:11 P |
| മേടം | 2006/04/14 | 06:15 A | 05:39 A |
| ഇടവം | 2006/05/15 | 03:08 A | 02:33 A |
| മിഥുനം | 2006/06/15 | 09:44 A | 09:14 A |
| കര്‍ക്കടകം | 2006/07/16 | 08:36 P | 08:09 P |
| ചിങ്ങം | 2006/08/17 | 05:00 A | 04:35 A |
| കന്നി | 2006/09/17 | 04:56 A | 04:33 A |
| തുലാം | 2006/10/17 | 04:53 P | 04:31 P |
| വൃശ്ചികം | 2006/11/16 | 04:41 P | 04:17 P |
| ധനു | 2006/12/16 | 07:19 A | 06:54 A |
ഇതില്‍ നിന്നു ഞാന്‍ മനസ്സിലാക്കുന്നതു താഴെപ്പറയുന്നവയില്‍ ഒന്നു സംഭവിച്ചിരിക്കാം എന്നാണു്:
ഈ അയനാംശം എന്നു പറയുന്നതെന്താണെന്നു പറയാന്‍ മറ്റൊരു പോസ്റ്റു വേണ്ടി വരും. (എനിക്കെന്നാണോ ഇതൊക്കെ എഴുതാന്‍ സമയം കിട്ടുക? 🙁 ) എങ്കിലും ചുരുക്കമായി പറയാം.
പാശ്ചാത്യര്‍ ഭൂമിയെ അപേക്ഷിച്ചു് സൂര്യനുള്ള ചലനത്തിന്റെ അടിസ്ഥാനത്തിലാണു് സംക്രമങ്ങള്‍ കണക്കാക്കുക. അവര്‍ക്കു് മാര്‍ച്ച് 21-നാണു മേടസംക്രമം. (First point of Aries). അന്നാണു് സൂര്യന്‍ ഭൂമദ്ധ്യരേഖ തെക്കു നിന്നു വടക്കോട്ടു മുറിച്ചുകടക്കുന്നതു്. അന്നാണു് ഭൂമിയിലെവിടെയും രാത്രിയും പകലും തുല്യദൈര്‍ഗ്ഘ്യത്തോടെ വരുന്നതു്. (സെപ്റ്റംബര്‍ 23-നും ഇതു സംഭവിക്കും – സൂര്യന്‍ വടക്കുനിന്നു തെക്കോട്ടു കടക്കുമ്പോള്‍ – തുലാസംക്രമം – First point of Libra). ശരിക്കു് വിഷു വരേണ്ടതു് ഈ ദിവസമാണു്, നിര്‍വ്വചനമനുസരിച്ചു്. കൂടുതല്‍ ശാസ്ത്രീയവും ഇതാണു്.
പക്ഷേ, സൂര്യനെ അപേക്ഷിച്ചു നക്ഷത്രങ്ങള്‍ സ്ഥിരമായി നില്‍ക്കുന്നു എന്നു കരുതിയ ഭാരതീയര്‍ നക്ഷത്രങ്ങളെയാണു് സ്ഥാനമാനത്തിനു് ഉപയോഗിച്ചതു്. ജ്യോതിശ്ചക്രത്തെ (360 ഡിഗ്രി) അവര്‍ ഇരുപത്തേഴായി വിഭജിച്ചു് ഓരോ ഭാഗവും (13 ഡിഗ്രി 20 മിനിട്ടു്) അവിടെയുള്ള ഓരോ നക്ഷത്രത്തിനു (അശ്വതി, ഭരണി തുടങ്ങിയവ) കൊടുത്തു. ഇതനുസരിച്ചു്, രേവതിയുടെയും അശ്വതിയുടെയും ഇടയ്ക്കുള്ള സ്ഥലം പൂജ്യം ഡിഗ്രിയിലും ചിത്തിരയുടെ മദ്ധ്യം 180 ഡിഗ്രിയിലുമായിരുന്നു.
ഇതു് ക്രി. പി. ആറാം നൂറ്റാണ്ടിലെ (ആര്യഭടന്റെ കാലം) കാര്യം. ലോകത്തില്‍ ഒന്നും സ്ഥിരമല്ല. ഇന്നു് അശ്വതിയുടെ ആദിക്കും ചിത്തിരയ്ക്കും ഇടയ്ക്കുള്ള ആംഗിള്‍ 180 ഡിഗ്രി അല്ല. അതുപോലെ തന്നെ മറ്റു നക്ഷത്രങ്ങളും. ഇവയില്‍ ഏതു നക്ഷത്രത്തെ അടിസ്ഥാനമാക്കി വേണം സ്ഥാനമാനം എന്നു് ഭാരതീയശാസ്ത്രജ്ഞന്മാര്‍ കലഹിക്കാന്‍ തുടങ്ങി. ഇന്നും ആ കലഹം തുടര്‍ന്നുകൊണ്ടിരിക്കുന്നു.
പാശ്ചാത്യരുടെ സൂര്യനെ അടിസ്ഥാനമാക്കിയുള്ള തിയറിയില്‍ നിന്നു് ഒരു പ്രത്യേകഭാരതീയമാനത്തിനു് എത്ര ഡിഗ്രി വ്യത്യാസമുണ്ടു് എന്ന അളവാണു് അയനാംശം. ഇതു പലര്‍ക്കും പലതാണു്. ഉദാഹരണമായി 2000 തുടങ്ങുമ്പോഴുള്ള പല അയനാംശങ്ങളും താഴെച്ചേര്‍ക്കുന്നു.
| ലാഹിരി | 23:51:41 |
| ബി. വി. രാമന്‍ | 22:24:11 |
| Fagan/Bradley | 24:44:11 |
| ഉഷ – ശശി | 20:03:26 |
| കൃഷ്ണമൂര്‍ത്തി | 23:45:06 |
| ദേവദത്ത | 23:28:34 |
ഇതനുസരിച്ചു് ഗ്രഹസ്ഫുടങ്ങള്‍ക്കും സംക്രമസമയങ്ങള്‍ക്കും (നക്ഷത്രം, ഞാറ്റുവേല തുടങ്ങിയവയ്ക്കും ഇതു ബാധകമാണു്) വ്യത്യാസമുണ്ടാകും. ഭാരതസര്‍ക്കാര്‍ അംഗീകരിച്ചരിക്കുന്നതു് (എന്റെ അറിവില്‍) ലാഹിരിയുടെ അയനാംശമാണു്.
അയനാംശം, അതു് ഏതു പദ്ധതിയാണെങ്കിലും, ഒരു സ്ഥിരസംഖ്യയല്ല. അതു കൂടിക്കൊണ്ടിരിക്കുന്നു.
ഞാന്‍ എന്റെ കണക്കുകൂട്ടലുകള്‍ക്കുപയോഗിച്ചിരിക്കുന്നതു് ലാഹിരിയുടെ അയനാംശമാണു്. കൃത്യമായിപ്പറഞ്ഞാല്‍, ലാഹിരിയുടെ പട്ടികകളില്‍ നിന്നു് ഞാന്‍ least square fitting ഉപയോഗിച്ചു് ഉണ്ടാക്കിയെടുത്ത
അയനാംശം =
എന്ന സൂത്രവാക്യം. ഇതില്‍ c എന്നതു് 2000 ജനുവരി 1 നട്ടുച്ച (GMT) മുതലുള്ള നൂറ്റാണ്ടുകളുടെ എണ്ണം (2000-ത്തിനു മുമ്പുള്ള തീയതികള്‍ക്കു് ഇതു നെഗറ്റീവായിരിക്കും.) ഒരു ഭിന്നമായി കൊടുത്തതാണു്.
ഈ അടുത്തകാലത്തു് കൃഷ്ണമൂര്‍ത്തിയുടെ പദ്ധതിയാണു “കൂടുതല്‍ ശരി” എന്നു് വളരെ ജ്യോത്സ്യന്മാര്‍ (ഭാവിഫലം ശരിയാകാനാണേ, ശാസ്ത്രത്തിനു വേണ്ടിയല്ല!) വാദിക്കുന്നുണ്ടു്.
എനിക്കു തോന്നുന്നതു് മാതൃഭൂമി ഇപ്പോള്‍ കൃഷ്ണമൂര്‍ത്തി പദ്ധതിയാണു് ഉപയോഗിക്കുന്നതു് എന്നാണു്.
ഇതു് തെറ്റെന്നു പറഞ്ഞുകൂടാ. എല്ലാം ഒരുപോലെ ശരിയാണു്. അഥവാ എല്ലാം ഒരുപോലെ തെറ്റും. ഇതില്‍ ഞാന്‍ പൂര്‍ണ്ണമായും നിഷ്പക്ഷനാണു്. കണ്‍ഫ്യൂഷന്‍ കുറവുള്ള പാശ്ചാത്യരീതിയോടാണു് എനിക്കു ചായ്‌വു്. പക്ഷേ ഭാരതീയര്‍ അതു സമ്മതിക്കുമെന്നു തോന്നുന്നില്ല.
മാതൃഭൂമി മിക്കവാറും വിശദീകരണം പ്രസിദ്ധീകരിച്ചേക്കും. ആരെങ്കിലും അതു കണ്ടാല്‍ ദയവായി ഇവിടെയൊരു കമന്റിടുക.
കുട്ട്യേടത്തി അയച്ചു തന്ന ഈ മനോരമ ലിങ്കിലെ വസ്തുതകളെപ്പറ്റിയുള്ള ആദ്യത്തെ പ്രതികരണമാണിതു്.
ഈ പോസ്റ്റിന്റെ കമന്റില്‍ ഞാന്‍ “മനോരമ എഴുതിയിരിക്കുന്നതു് ടോട്ടല്‍ നോണ്‍സെന്‍സ് ആണു്…” എന്നെഴുതിയിരുന്നു. അതു തെറ്റാണു്. പതിനാറു കൊല്ലം മുമ്പുണ്ടായ ഒരു തര്‍ക്കത്തിന്റെ മുന്‍‌വിധിയില്‍ കണക്കൊന്നും കൂട്ടാതെ പറഞ്ഞതാണു്. ക്ഷമിക്കുക.
മനോരമ പറയുന്നതിലും കാര്യമുണ്ടു്. എങ്കിലും അവര്‍ പറയുന്നതു മുഴുവനും ശരിയല്ല. വിഷു 14-നു തന്നെ.
ഞാന്‍ ജ്യോതിശ്ശാസ്ത്രം, കലണ്ടര്‍, കൊല്ലവര്‍ഷം തുടങ്ങിയവയുടെ ഗണിതക്രിയകള്‍ ഉള്‍ക്കൊള്ളുന്ന ഏതാനും കമ്പ്യൂട്ടര്‍ പ്രോഗ്രാമുകള്‍ എഴുതിയിട്ടുണ്ടു്. മറ്റു പല രീതികള്‍ പോലെ interpolation പോലെയുള്ള ഏകദേശരീതികള്‍ ഉപയോഗിച്ചല്ല, ആധുനികശാസ്ത്രത്തിന്റെ ഡാറ്റ ഉപയോഗിച്ചാണു് ഇതുണ്ടാക്കിയിട്ടുണ്ടു്. ലോകത്തു പല സ്ഥലത്തു നിന്നും ഇറങ്ങുന്ന അല്‍മനാക്കുകളും പഞ്ചാംഗങ്ങളും ഉപയോഗിച്ചു് ഇതിന്റെ സാധുത സ്ഥിരീകരിച്ചിട്ടുണ്ടു്.
ഇതിന്റെ വെളിച്ചത്തില്‍ മുകളില്‍ പറയുന്ന നാലു വസ്തുതകളെ ഒന്നു പരിശോധിക്കട്ടേ.
| സ്ഥലം | അക്ഷാംശം | രേഖാംശം | ഉദയം | മനോരമ |
| (ഡിഗ്രി:മിനിട്ട് N) | (ഡിഗ്രി:മിനിട്ട് E) | (AM IST) | (AM IST) | |
| പാറശ്ശാല | 08:28 | 76:55 | 06:17 | |
| തിരുവനന്തപുരം | 08:29 | 76:59 | 06:17 | 06:17 |
| ശബരിമല | 09:22 | 76:49 | 06:17 | |
| കൊച്ചി | 09:58 | 76:17 | 06:18 | 06:18 |
| ആലുവ | 10:07 | 76:24 | 06:18 | |
| ഗുരുവായൂര്‍ | 09:34 | 76:31 | 06:18 | 06:18 |
| പാലക്കാടു് | 10:46 | 76:39 | 06:16 | |
| കോഴിക്കോടു് | 11:15 | 75:49 | 06:19 | 06:20 |
| കണ്ണൂര്‍ | 11:52 | 75:25 | 06:20 | 06:20 |
| കാസര്‍കോടു് | 12:30 | 75:00 | 06:22 | 06:22 |
ഇതില്‍ നിന്നു ഞാന്‍ മനസ്സിലാക്കുന്നതു് ഇതാണു്: മാതൃഭൂമി പഞ്ചാംഗം ഗണിച്ച വി. പി. കെ. പൊതുവാളിനു് ഒരു വലിയ അബദ്ധം പറ്റിപ്പോയി. മനോരമ അതു കണ്ടുപിടിച്ചു. തൊണ്ണൂറുകളുടെ ആദ്യം സംഭവിച്ച ക്ഷീണം വിട്ടുമാറാത്ത (അന്നു് ഇതുപോലൊരു തര്‍ക്കമുണ്ടായിട്ടു് മാതൃഭൂമിയുടെ വാദമാണു ശരിയെന്നു തീരുമാനമുണ്ടായി) മനോരമ ഈ അവസരം ശരിക്കു വിനിയോഗിച്ചു. പക്ഷേ ഇതു മൂലം വിഷുവിന്റെ തീയതി തെറ്റിയിട്ടില്ല. സര്‍ക്കാരിന്റെ കലണ്ടറിലെ തെറ്റു് വികലമായ കണക്കുകൂട്ടലിന്റെ ഫലമാണു്.
തമിഴ്‌നാട്ടില്‍ 15-നാണു വിഷുക്കണി എന്നു മനോരമ പറയുന്നതു ശരിയാണു്. കുറച്ചുകൂടി കിഴക്കുള്ള അവര്‍ക്കു സൂര്യന്‍ അല്പം നേരത്തെ ഉദിക്കും. അതുകൊണ്ടു് സൂര്യോദയത്തിനു ശേഷമേ മേടസംക്രമം ഉണ്ടാവുകയുള്ളൂ.
അതിനാല്‍, കേരളത്തിലും അതിനു പടിഞ്ഞാറോട്ടു് അമേരിക്ക വരെയുള്ളവര്‍ 14-നു തന്നെ വിഷു ആഘോഷിച്ചു കൊള്ളൂ. കേരളത്തിനു കിഴക്കുള്ളവള്‍ 15-നാണെന്നു തോന്നുന്നു. വക്കാരി ഏതായലും 14-നു തന്നെ ആഘോഷിക്കൂ. 15-നു വേണോ എന്നു് ഞാന്‍ ഒരു ദിവസത്തിനകം പറയാം.
തോന്നുന്നു എന്നു പറഞ്ഞതു് എന്റെ അറിവുകേടു കൊണ്ടാണു്. വിഷു എന്നും മേടം 1-നാണെന്നാണു ഞാന്‍ കരുതിയിരുന്നതു്. അല്ലെന്നു തോന്നുന്നു. വിശദമായി അന്വേഷിച്ചതിനു ശേഷം അതിനെപ്പറ്റി എഴുതാം. മേടം 1 ഏതായാലും 14-നു തന്നെ.
വര്‍ഷങ്ങള്‍ക്കു മുമ്പുണ്ടായിരുന്ന തര്‍ക്കം ഒന്നാം തീയതിയെപ്പറ്റിയായിരുന്നു. വിഷുവാണോ ആണ്ടുപിറപ്പാണോ (ചിങ്ങം 1) എന്നു് ഓര്‍മ്മയില്ല.
മലയാളമാസം ഒന്നാം തീയതി കണ്ടുപിടിക്കുന്നതു് ഇങ്ങനെയാണു്:
സൂര്യന്‍ മീനത്തില്‍ നിന്നു മേടത്തിലേക്കു കടക്കുന്നതു് (മേടസംക്രമം) എപ്പോഴാണെന്നു നോക്കുക. (കലണ്ടറില്‍ കാണും. അല്ലെങ്കില്‍ കണക്കുകൂട്ടുക.)
ഈ സമയം മദ്ധ്യാഹ്നം കഴിയുന്നതിനു മുമ്പാണെങ്കില്‍, ആ ദിവസം തന്നെ ഒന്നാം തീയതിയും വിഷുവും. മദ്ധ്യാഹ്നത്തിനു ശേഷമാണെങ്കില്‍ പിറ്റേന്നും.
ഇനി, “മദ്ധ്യാഹ്നം കഴിയുക” എന്നു വെച്ചാല്‍ നട്ടുച്ച കഴിയുക എന്നല്ല. ഒരു പകലിനെ അഞ്ചായി വിഭജിച്ചതിന്റെ (പ്രാഹ്ണം, പൂര്‍വാഹ്നം, മദ്ധ്യാഹ്നം, അപരാഹ്നം, സായാഹ്നം) മൂന്നാമത്തെ അഹ്നമാണു മദ്ധ്യാഹ്നം. അതുകൊണ്ടു “മദ്ധ്യാഹ്നം കഴിയുക” എന്നു പറഞ്ഞാല്‍ ദിവസത്തിന്റെ അഞ്ചില്‍ മൂന്നു സമയം കഴിയുക എന്നാണു്. ഉദയവും അസ്തമയവും എപ്പോഴെന്നു നോക്കീട്ടു കണക്കാക്കണം. (ലോകത്തിന്റെ പല ഭാഗത്തു് ഇതു പല സമയത്താണെന്നു് ഓര്‍ക്കണം.) ആറു മണി മുതല്‍ ആറു മണി വരെയുള്ള ഒരു പകലില്‍ ഇതു് ഏകദേശം 1:12 PM-നു് ആയിരിക്കും. (ഇതായിരുന്നു മാതൃഭൂമിയും മനോരമയും തമ്മിലുള്ള തര്‍ക്കം. മനോരമ ഉച്ച എന്നു കരുതി. ആ വര്‍ഷം സംക്രമം 12 മണിക്കും 1:12-നും ഇടയ്ക്കായിരുന്നു)
പിന്നെ, വടക്കേ മലബാറില്‍ ഈ പ്രശ്നമൊന്നുമില്ല. അവിടെ എപ്പോഴും പിറ്റേ ദിവസമാണു് ഒന്നാം തീയതി. ഇതും മാതൃഭൂമി കലണ്ടറില്‍ കാണാം. “വടക്കേ മലബാറില്‍ ചിങ്ങം … ദിവസം. … -നു കന്നി 1.” എന്നിങ്ങനെ. സൂക്ഷിച്ചു നോക്കിയാല്‍, ആ മാസങ്ങളുടെ സംക്രമം മദ്ധ്യാഹ്നം കഴിയുന്നതിനു മുമ്പാണെന്നു കാണാം.
പൊതുവാള്‍ അല്പം കൂടി ശ്രദ്ധിക്കേണ്ടിയിരുന്നു. ഇതുവരെ മാതൃഭൂമി കലണ്ടറിനെ വലിയ വിശ്വാസവും ബഹുമാനവുമായിരുന്നു. (നാട്ടില്‍ പോയ ഒരു സുഹൃത്തിനോടു പറഞ്ഞു് ഇന്നലെ ഒന്നു കിട്ടിയതേ ഉള്ളൂ.) അതു പോയിക്കിട്ടി.
മനോരമയും അതേ ഉദ്ദേശിച്ചിട്ടുള്ളൂ എന്നു തോന്നുന്നു.
(ദയവായി ഇതുകൂടി വായിക്കുക.)
ഗണിതശാസ്ത്രത്തിനു ദക്ഷിണഭാരതത്തിന്റെ – പ്രത്യേകിച്ചു കേരളത്തിന്റെ – സംഭാവനകളിലൊന്നായ പരല്‍പ്പേരിനെപ്പറ്റി ഞാന്‍ ഇവിടെ എഴുതിയ ലേഖനങ്ങള്‍ (1, 2)അധികം ആളുകള്‍ക്കും അജ്ഞാതമായിരുന്ന ആ രീതിയെ പരിചയപ്പെടുത്താന്‍ ഉപകരിച്ചു എന്നറിഞ്ഞതില്‍ സന്തോഷം. ആ ലേഖനങ്ങള്‍ താഴെപ്പറയുന്നവയ്ക്കു പ്രചോദനമായതില്‍ അതിലും സന്തോഷം.
കെവിന്റെ പ്രോഗ്രാം ഒരു നല്ല കൊച്ചു പ്രോഗ്രാമാണു്. നന്ദി കെവിന്‍. ഇതിനെ അടിസ്ഥാനമാക്കി ആരെങ്കിലും ഒരു വെബ് പ്രോഗ്രാം കൂടി എഴുതുമോ – PHP-യിലോ മറ്റോ?
ഗുരുകുലം വീണ്ടും സ്ഥലം മാറി. ഇവിടെ നിന്നു് ഇവിടേയ്ക്കു്.
ബുക്ക്മാര്‍ക്കു ചെയ്തിട്ടുണ്ടെങ്കില്‍ ദയവായി തിരുത്തുക.
ആധുനികഭാരതത്തിലെ ഏറ്റവും മഹാനായ ഗണിതശാസ്ത്രജ്ഞനായിരുന്നു ശ്രീനിവാസരാമാനുജന്‍. നമ്മുടെ അശാസ്ത്രീയമായ വിദ്യാഭ്യാസസമ്പ്രദായത്തിന്റെ ബലിയാടായി പരീക്ഷകളില്‍ തോല്‍ക്കുകയും ക്ലാസ്സുകയറ്റം നിഷേധിക്കപ്പെടുകയും ചെയ്തു്, പില്‍ക്കാലത്തു ലോകത്തെമ്പാടുമുള്ള ഗണിതശാസ്ത്രജ്ഞരെ അമ്പരപ്പിച്ച (ഇന്നും അമ്പരപ്പിച്ചുകൊണ്ടിരിക്കുന്ന) സിദ്ധാന്തങ്ങള്‍ തന്റെ പഴയ വീട്ടിലെ ബെഞ്ചിലിരുന്നു് തന്റെ നോട്ടുബുക്കുകളില്‍ കുറിച്ചിട്ട അസാമാന്യപ്രതിഭാശാലി. ജി. എച്ച്. ഹാര്‍ഡി കണ്ടെത്തിയിരുന്നില്ലെങ്കില്‍ ഇന്നും ഈ “കാന്തിയും മൂല്യവും വാച്ചിടും” രത്നം “ചാണ കാണാതെ” ഭാരതാംബയുടെ കുക്ഷിയില്‍ മറഞ്ഞുപോയേനേ.
രാമാനുജനെപ്പറ്റിയുള്ള കഥകള്‍ പലപ്പോഴും അതിഭാവുകത്വത്തിലേക്കു കടക്കാറുണ്ടു്. പലപ്പോഴും അദ്ദേഹത്തിന്റെ ഗണിതശാസ്ത്രജ്ഞാനത്തെയും കഴിവിനെയും സത്യസന്ധമായി വിശകലനം ചെയ്യുന്നതിനു പകരം, അദ്ദേഹത്തെ ഒരു അമാനുഷനാക്കുന്ന കഥകളാണു നാം കേള്‍ക്കുന്നതു്.
ഇതിനു് ഒരു നല്ല ഉദാഹരണമാണു് രാമാനുജനും 1729 എന്ന സംഖ്യയും ഉള്‍പ്പെടുന്ന ഈ സംഭവം. ഹാര്‍ഡി പറയുന്നു:
I remember once going to see him when he was ill at Putney. I had ridden in taxi cab number 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavurable omen. “No,” he replied, “it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways.”
അതായതു്, രോഗശയ്യയിലായിരുന്ന രാമാനുജനോടു് ഹാര്‍ഡി 1729 (ഹാര്‍ഡി സഞ്ചരിച്ച ടാക്സിയുടെ നമ്പര്‍) ഒരു ചീത്ത സംഖ്യയാണു് എന്നു പറഞ്ഞപ്പോള്‍, അതു് രണ്ടു ഘനസംഖ്യകളുടെ തുകയായി രണ്ടു വിധത്തിലെഴുതാവുന്ന ഏറ്റവും ചെറിയ സംഖ്യയാണെന്നു് രാമാനുജന്‍ ഉത്തരം പറഞ്ഞു.
ഇത്രയും നടന്ന കാര്യം. (യുക്തിവാദിയായിരുന്ന ഹാര്‍ഡി unfavourable omen എന്നു പറഞ്ഞതു് വിശ്വാസിയായ രാമാനുജനോടായതുകൊണ്ടാവാം.) ഇതില്‍നിന്നു വീരഗാഥയെഴുതുന്ന പാണന്മാര്‍ കണ്ടെത്തുന്നതു് ഏതു സംഖ്യ കിട്ടിയാലും ഞൊടിയിടയ്ക്കുള്ളില്‍ അതിന്റെ ഇത്രയും ദുര്‍ഗ്രഹമായ പ്രത്യേകതകള്‍ കണ്ടുപിടിക്കാന്‍ പറ്റുന്ന അസാമാന്യപ്രതിഭ എന്നാണു്.
സത്യത്തില്‍ രാമാനുജനു് 1729-ന്റെ ഈ പ്രത്യേകത നേരത്തേ അറിയാമായിരുന്നു. രാമാനുജന്റെ അവസാനത്തെ നോട്ടുബുക്ക് എവിടെയോ വെച്ചു നഷ്ടമായതു് അദ്ദേഹം മരിച്ചു വളരെക്കാലം കഴിഞ്ഞാണു് (1965-ല്‍) കണ്ടെടുക്കുന്നതു്. ഇതിലെ സിദ്ധാന്തങ്ങള്‍ ഇന്നും ദുര്‍ഗ്രഹങ്ങളായി നിലകൊള്ളുന്നു. 1987-ല്‍ Tata Institute of Fundamental Research-ഉം Narosa Publishers-ഉം ചേര്‍ന്നു് രാമാനുജന്റെ നഷ്ടപ്പെട്ട കുറിപ്പുകള്‍ (Lost Notebook) ഫോട്ടോസ്റ്റാറ്റ് രൂപത്തില്‍ പ്രസിദ്ധീകരിച്ചു. അതിന്റെ 341-ാ‍ം പേജില്‍ ഇങ്ങനെ കാണാം:
If
then
Examples:
അവസാനത്തേതിനു തൊട്ടുമുമ്പിലുള്ള ഉദാഹരണം ശ്രദ്ധിക്കൂ. 1729 ആണു് അതിന്റെ മൂല്യം. ഈ സിദ്ധാന്തത്തെപ്പറ്റി പഠിച്ച സമയത്തു് 1729-ന്റെ ഈ പ്രത്യേകത രാമാനുജന്‍ ശ്രദ്ധിച്ചിട്ടുണ്ടാവണം. അതു് ആ സന്ദര്‍ഭത്തില്‍ പറഞ്ഞിട്ടുമുണ്ടാവണം. രോഗശയ്യയായിരുന്നതിനാല്‍ സംസാരവിഷയം പെട്ടെന്നു മാറിപ്പോയിട്ടുണ്ടാവണം. രാമാനുജന്റെ മരണത്തിനു ശേഷമായിരിക്കണം ഹാര്‍ഡി ഇതു പിന്നെ ഓര്‍ത്തതും രേഖപ്പെടുത്തിയതും. ഹാര്‍ഡിക്കോ പിന്നെ ചരിത്രം രേഖപ്പെടുത്തിയവര്‍ക്കോ രാമാനുജനെഴുതിയ ഈ കുറിപ്പുകളെപ്പറ്റി അറിവുണ്ടായിരുന്നില്ല. 1987-നു ശേഷവും ആരെങ്കിലും ഇതു ശ്രദ്ധിച്ചതായി എനിക്കറിവില്ല.
ഇനി, ഈ സിദ്ധാന്തം ശ്രദ്ധിക്കൂ. ഇതെങ്ങനെ കിട്ടിയെന്നോ, ഇതെങ്ങനെ തെളിയിക്കുമെന്നോ, ഇതില്‍ നിന്നു് മേല്‍പ്പറഞ്ഞ ഉദാഹരണങ്ങള്‍ എങ്ങനെ ഉണ്ടാക്കിയെടുക്കുമെന്നോ എനിക്കു വലിയ പിടിയില്ല. അവിടെയാണു് ഗവേഷണം ആവശ്യമാവുന്നതു്. അവിടെയാണു് രാമാനുജന്റെ പ്രതിഭ കുടികൊള്ളുന്നതു്. ഒരു അജ്ഞാതസംഖ്യയെപ്പറ്റി ഞൊടിയിടയ്ക്കുള്ളില്‍ ഒരു സിദ്ധാന്തം “ഉണ്ടാക്കിയെടുത്തതില്‍” അല്ല.
കഴിഞ്ഞ രണ്ടു ലേഖനങ്ങളില്‍ കൊടുത്തിരുന്ന പ്രശ്നങ്ങള്‍
(”അര്‍ജ്ജുനന്റെ അമ്പുകളും“, “അരയന്നങ്ങളും“) quadratic equations
ഉണ്ടാക്കി നിര്‍ദ്ധരിക്കാന്‍ ഏതു സ്കൂള്‍കുട്ടിക്കും കഴിയും. കണ്ടുപിടിക്കേണ്ട മൂല്യം (അമ്പുകളുടെ എണ്ണമോ, അരയന്നങ്ങളുടെ എണ്ണമോ) x2 എന്നു സങ്കല്‍പ്പിച്ചാല്‍ ആദ്യത്തേതില്‍ നിന്നു്
എന്നും, രണ്ടാമത്തേതില്‍ നിന്നു്
എന്നുമുള്ള സമവാക്യങ്ങള്‍ ഉണ്ടാക്കി
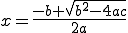
എന്നസൂത്രവാക്യം ഉപയോഗിച്ചാല്‍ 10 എന്നും 4 എന്നുമുള്ള ഉത്തരങ്ങള്‍ കിട്ടും. (-2 എന്നും 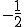എന്നും രണ്ടുത്തരങ്ങള്‍ കൂടിയുണ്ടു്‌. അതിവിടെ പ്രസക്തമല്ലാത്തതുകൊണ്ടു്‌ ഉപേക്ഷിച്ചു.) അപ്പോള്‍ 100 അമ്പുകള്‍, 16 അരയന്നങ്ങള്‍.
ഇനി, ഭാസ്കരാചാര്യരുടെ സൂത്രവാക്യം നോക്കാം.
അതായതു്, 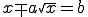എന്നതില്‍ നിന്നു്
ഉദാഹരണമായി,
ഇങ്ങനെ സാമാന്യനിയമം പറയുന്നതുകൂടാതെ, Quadratic equation നിര്‍ദ്ധരിക്കേണ്ട മറ്റു പ്രശ്നങ്ങള്‍ ഈ സൂത്രം ഉള്‍ക്കൊള്ളിച്ചു തന്നെ നിയമങ്ങള്‍ അദ്ദേഹം നല്‍കിയിട്ടിട്ടുണ്ടു്‌. ഉദാഹരണത്തിനു്‌, ഒരു സമാന്തരശ്രേഢി (Arithmetic Progression)യിലെ ആദ്യപദവും (മുഖം, a), പൊതുവ്യത്യാസവും (ചയം, d), ആദ്യത്തെ n (ഗച്ഛം) പദങ്ങളുടെ തുകയും (ഫലം, S) തന്നാല്‍ n കണ്ടുപിടിക്കാന്‍
എന്ന Quadratic equation n-നു വേണ്ടി നിര്‍ദ്ധരിക്കേണ്ടി വരും.
ഭാസ്കരാചാര്യരുടെ രീതി നോക്കൂ:
അതായതു്,
ഭാസ്കരാചാര്യരുടെ ഉദാഹരണം നോക്കുക:
ഇവിടെ ഫലം = 360, മുഖം = 3, ചയം = 2.
ചയത്തിന്റെ ഇരട്ടി = 2 x 2 = 4, അതുകൊണ്ടു ഫലത്തെ ഗുണിച്ചാല്‍ 360 x 4 = 1440, ചയത്തിന്റെ പകുതി = 1, അതു മുഖത്തില്‍ നിന്നു കുറച്ചാല്‍ 3 – 1 = 2, അതിന്റെ വര്‍ഗ്ഗം = 4, അതു കൂട്ടിയാല്‍ 1444. വര്‍ഗ്ഗമൂലം 38. മുഖം കുറച്ചാല്‍ 38 – 3 = 35, ചയത്തിന്റെ പകുതി കൂട്ടിയാല്‍ 35 + 1 = 16, ചയം കൊണ്ടു ഹരിച്ചാല്‍ 36 / 2 = 18. ഗച്ഛം (n) = 18.
സൂക്ഷിച്ചുനോക്കിയാല്‍
അതായതു് എന്ന Quadratic equation-ന്റെ നിര്‍ദ്ധാരണം തന്നെയാണു്‌ ഈ രീതിയെന്നു കാണാം.
ഇംഗ്ലീഷ്‌ വിക്കിപീഡിയയില്‍ ഭാസ്കരാചാര്യരുടെ ഈ രീതി പരാമര്‍ശിച്ചിട്ടുണ്ടു്‌.
വര്‍ഗ്ഗീകരണം പൂര്‍ത്തിയാക്കി quadratic equations നിര്‍ദ്ധരിക്കുന്ന വിദ്യ ബാബിലോണിയക്കാര്‍ക്കു ക്രി. മു. നാലാം നൂറ്റാണ്ടില്‍ അറിയാമായിരുന്നു എന്നു് വിക്കിപീഡിയ പറയുന്നു. ഈ രീതി തന്നെയാണു ഭാസ്കരാചാര്യരും ഉപയോഗിച്ചിട്ടുള്ളതു്.
നിര്‍ദ്ധരിക്കേണ്ട സമവാക്യം
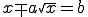
എന്നാണല്ലോ. ഇതിനെ 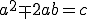എന്നു കരുതിയിട്ടു്, രണ്ടിനോടും
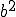കൂട്ടി ഇടത്തുവശത്തുള്ളതിനെ ഒരു പൂര്‍ണ്ണവര്‍ഗ്ഗമാക്കുന്നതാണു് ഈ രീതി. അതായതു്,
വര്‍ഗ്ഗമൂലമെടുത്താല്‍
അപ്പോള്‍
എന്നു കിട്ടും. ഇതാണു ഭാസ്കരാചാര്യരുടെ ഗുണഘ്നമൂലോന… എന്ന ശ്ലോകത്തിന്റെ അര്‍ത്ഥം.
ഭാസ്കരാചാര്യരുടെ (ഭാസ്കരന്‍ II – ക്രി. പി. 12-ാ‍ം ശതകം) ലീലാവതിയില്‍ നിന്നു മറ്റൊരു പ്രശ്നം:
കുട്ടീ, അരയന്നങ്ങളുടെ വര്‍ഗ്ഗമൂലത്തിന്റെ (square root) പകുതിയുടെ ഏഴിരട്ടി തീരത്തുകൂടി കുണുങ്ങിക്കുണുങ്ങി നടന്നു. ബാക്കിയുള്ള രണ്ടെണ്ണം കളിയും ചിരിയും വഴക്കുമൊക്കെയായി വെള്ളത്തില്‍ത്തന്നെയും കഴിഞ്ഞു. (വാലന്റൈന്‍സ്‌ ഡേ ആയതുകൊണ്ടായിരിക്കണം) എന്നാല്‍ ആകെ എത്ര അരയന്നങ്ങളുണ്ടായിരുന്നു?
Quadratic equation നിര്‍ദ്ധരിക്കാനുള്ള ഒരു പ്രശ്നമാണിതു്‌. ഇതിന്റെ ആധുനികഗണിതം ഉപയോഗിച്ചുള്ള നിര്‍ദ്ധാരണവും, ഭാസ്കരാചാര്യരുടെ രീതിയും താമസിയാതെ ഇവിടെ ചേര്‍ക്കാം. അതുവരെ നിങ്ങളൊന്നു ശ്രമിച്ചുനോക്കൂ.
ഭാസ്കരാചാര്യരുടെ (ഭാസ്കരന്‍ II – ക്രി. പി. 12-ാ‍ം ശതകം) ലീലാവതിയില്‍ നിന്നൊരു പ്രശ്നം:
Quadratic equation നിര്‍ദ്ധരിക്കാനുള്ള ഒരു പ്രശ്നമാണിതു്‌. ഇതിന്റെ ആധുനികഗണിതം ഉപയോഗിച്ചുള്ള നിര്‍ദ്ധാരണവും, ഭാസ്കരാചാര്യരുടെ രീതിയും താമസിയാതെ ഇവിടെ ചേര്‍ക്കാം. അതുവരെ നിങ്ങളൊന്നു ശ്രമിച്ചുനോക്കൂ.
February 14th, 2006 at 8:41 pm
100 എന്നാണു എന്റെ ഉത്തരം. അഥവാ ശരിയാണെങ്കില്‍ പൊട്ടഭാഗ്യത്തിനു 100 മാര്‍ക്കു കൊടുത്തോള്ളൂ.
February 14th, 2006 at 9:14 pm
ഇതില്‍ എന്താ ഇത്ര കുടുക്ക് എന്നു മനസ്സിലായില്ല!
let N = x^2 be the number of arrows.
Then we have
x^2 – 8x -20 = 0
from which, a positive root is x=10.
so N = 100
ശരിയല്ലേ? അതോ ഇനി വല്ല കുഴപ്പവുമുണ്ടോ?
February 14th, 2006 at 9:23 pm
ആധുനിക ഗണിതത്തിനു ഇതൊരു കുടുക്കല്ലല്ലോ വിശ്വം. ഭാസ്കരാചര്യര്‍ക്കു എപ്രകാരം വിഷമമായിരുന്നു എന്നുള്ളതു ഉമേഷ് വിശദീകരിക്കുമ്പോള്‍ അറിയാം.
February 14th, 2006 at 9:26 pm
എനിക്ക് ഓര്‍മ്മ വരുന്നില്ല പെട്ടെന്ന്. പക്ഷേ ഒരിക്കല്‍ ഞാന്‍ ചെയ്തിരുന്നൂന്നു മാത്രം ഓര്‍മ്മയുണ്ട്!
വയസ്സായിത്തുടങ്ങി…!
🙁
February 14th, 2006 at 9:32 pm
കുടുക്കൊന്നുമില്ല വിശ്വം. ആറാം ക്ലാസ്സിലെ കുട്ടി ചെയ്യും ഇതു്.
രണ്ടു കാരണങ്ങള്‍ കൊണ്ടാണു് ഇതിവിടെ ചേര്‍ത്തതു്‌
1) മനോഹരമായി പ്രശ്നങ്ങള്‍ പദ്യരൂപത്തില്‍ ഭാസ്കരാചാര്യര്‍ അവതരിപ്പിക്കുന്നതു കാണിക്കാന്‍.
2) 12-ാ‍ം നൂറ്റാണ്ടിലും (അതിനു മുമ്പും) ഇതൊക്കെ ചെയ്യാനറിയുന്നവര്‍ ഭാരതത്തിലുണ്ടായിരുന്നു എന്നു കാണിക്കാന്‍. “ലീലാവതി” ഒരുപാടു കാലം ടെക്സ്റ്റുബുക്കായിരുന്നു.
നിങ്ങളുടെ ഉത്തരം ശരി തന്നെ. ഭാസ്കരാചാര്യര്‍ ഇതിനു് ഒട്ടും പണിപ്പെട്ടിട്ടില്ല പെരിങ്ങോടരേ. നീറ്റായി ഒരു ഫോര്‍മുല തന്നിട്ടുണ്ടു മൂപ്പര്‍. അടുത്ത പോസ്റ്റും ഒരു quadratic equation ആണു്. അതുകൂടി കഴിഞ്ഞു്‌ ഭാസ്കരാചാര്യരുടെ രീതിയും മറ്റും ഈ രണ്ടു ചോദ്യങ്ങള്‍ക്കും വിശദീകരിക്കാം.
ഭാസ്കരാചര്യരും അതിനു മുമ്പു ബ്രഹ്മഗുപ്തനും സോള്‍വു ചെയ്തതും, പാശ്ചാത്യര്‍ക്കു പിന്നെയും നാലഞ്ചു നൂറ്റാണ്ടു കൂടി വേണ്ടി വന്നതും, നമ്മളില്‍ മിക്കവര്‍ക്കും ഇപ്പോഴും ചെയ്യാന്‍ പറ്റാത്തതുമായ ചിലതു്‌ ഇനി വരുന്നുണ്ടു്‌. ജാഗ്രതൈ!
February 15th, 2006 at 5:13 am
കാളിദാസന്റേതായി ഇതുപോലൊരു ശ്ലോകമില്ലേ? “ബാലേ” എന്നു തുടങ്ങുന്നതാണെന്നാണെന്റെ ഓര്‍മ്മ.
February 15th, 2006 at 8:50 am
ഉത്തരം ആരെങ്കിലും വരുന്നതിനു മുന്‍പു പറഞ്ഞിട്ടോടാം
അല്ലെങ്കില്‍ ‘ചാടാം’ പരല്‍പ്പേരു പഠിച്ചോന്നും നോക്കാലോ
February 15th, 2006 at 9:01 am
ഇലയും പക്ഷിയുമായുമോ മറ്റോ ഒരു simultaneous സമവാക്യത്തിന്റെ ശ്ലോകം കൂടെ കേട്ടിട്ടുണ്ടല്ലോ ഉമേഷേ. എന്താണതു്‌? പക്ഷികളിരട്ടയായിരുന്നാല്‍ ഒരില ബാക്കി. ഒറ്റയായിരുന്നാലൊരു പക്ഷി ബാക്കി എന്നാണര്‍ഥം
February 15th, 2006 at 3:09 pm
“ചാടി“യതു ശരിയായി സിദ്ധാര്‍ത്ഥാ. അപ്പോ പരല്‍പ്പേരു പഠിച്ചു, ല്ലേ?
മറ്റേ കണക്കു കേട്ടിട്ടുണ്ടു് (ഓരോ പക്ഷിയിരുന്നാല്‍ ഒരു പക്ഷി ബാക്കി, ഈരണ്ടു പക്ഷിയിരുന്നാല്‍ ഒരു മരം ബാക്കി – 4 പക്ഷി, 3 മരം എന്നുത്തരം.), ശ്ലോകം കേട്ടിട്ടില്ല.
കാളിദാസന്റെ ശ്ലോകം കേട്ടിട്ടില്ല. ഇതിനെ കാളിദാസന്റേതെന്നു് ആരോ പറഞ്ഞതായിരിക്കും.
അതോ, ഈ സമസ്യാപൂരണമാണോ?
കുസുമേ കുസുമോത്പത്തി
ശ്രൂയതേ വാ ന ദൃശ്യതേ
ബാലേ, തവ മുഖാംഭോജാ-
ദക്ഷിരിന്ദീവരദ്വയം!
അതോ, ഇതോ?
കാ ത്വം ബാലേ? കാഞ്ചനമാലാ;
കസ്യാഃ പുത്രീ? കനകലതായാഃ;
കിം തേ ഹസ്തേ? താലീപത്രം;
കാ വാ രേഖാ? ക ഖ ഗ ഘ;
രണ്ടും കാളിദാസന്റെയാണെന്നാണു കേട്ടിട്ടുള്ളതു്. ഇതു രണ്ടുമേ കാളിദാസന്റെ “ബാലേ” എന്നുള്ള ശ്ലോകം ഓര്‍മ്മ വരുന്നുള്ളൂ.
February 17th, 2006 at 11:21 pm
എല്ലാ ദിവസവും ഇവിടെ വന്നു നോക്കുന്നുണ്ട്. പഴയപോലെ ഗംഭീരമായി തുടങ്ങിവെച്ച് ഗംഭീരമായി ഉഴപ്പാനാണോ ഭാവം? എങ്കില്‍ ഞങ്ങള്‍ വെറുതെ വിടില്ല!
😉
February 18th, 2006 at 12:47 am
ആരംഭശൂരത്വത്തിനു ഞാന്‍ കുപ്രസിദ്ധനാണു വിശ്വം. എങ്കിലും കഴിയുന്നതു ശ്രമിക്കാം. ഓഫീസിലെ തിരക്കുകള്‍, മകന്റെ പിറന്നാള്‍ തുടങ്ങിയവ മൂലം സമയക്കുറവുണ്ടു്‌. എങ്കിലും അടുത്ത പോസ്റ്റിട്ടിട്ടുണ്ടു്‌. ഇവിടെ നോക്കൂ.
വിശ്വത്തിന്റെ കമന്റുകളില്‍ നിന്നു പ്രചോദനമുള്‍ക്കൊണ്ടു്‌ കലിദിനസംഖ്യയെപ്പറ്റി രണ്ടുമൂന്നു്‌ നെടുങ്കന്‍ പോസ്റ്റുകള്‍ ഉടനേ പ്രതീക്ഷിക്കാം. മൊത്തം എഴുതിയിട്ടേ പ്രസിദ്ധീകരിക്കൂ.