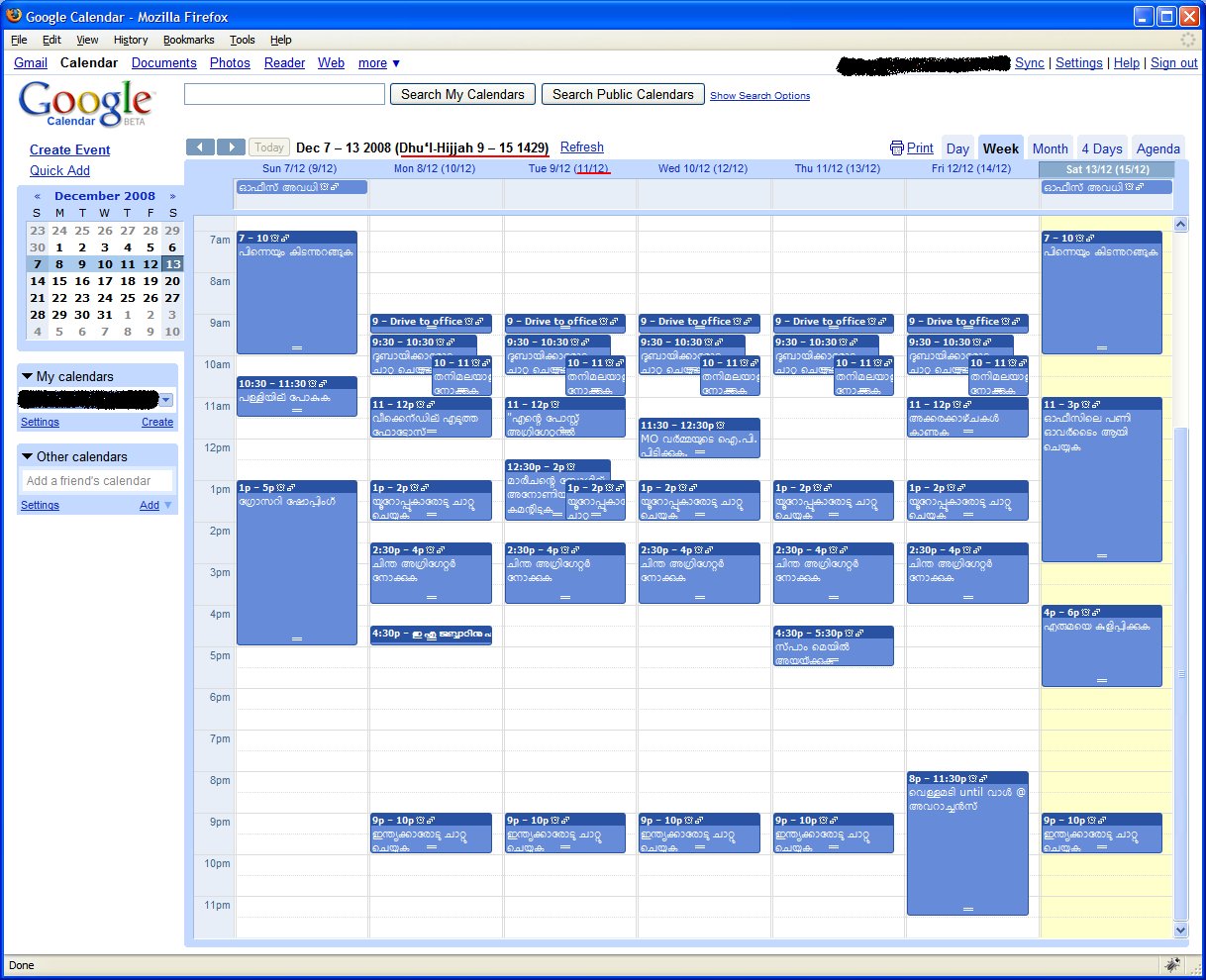
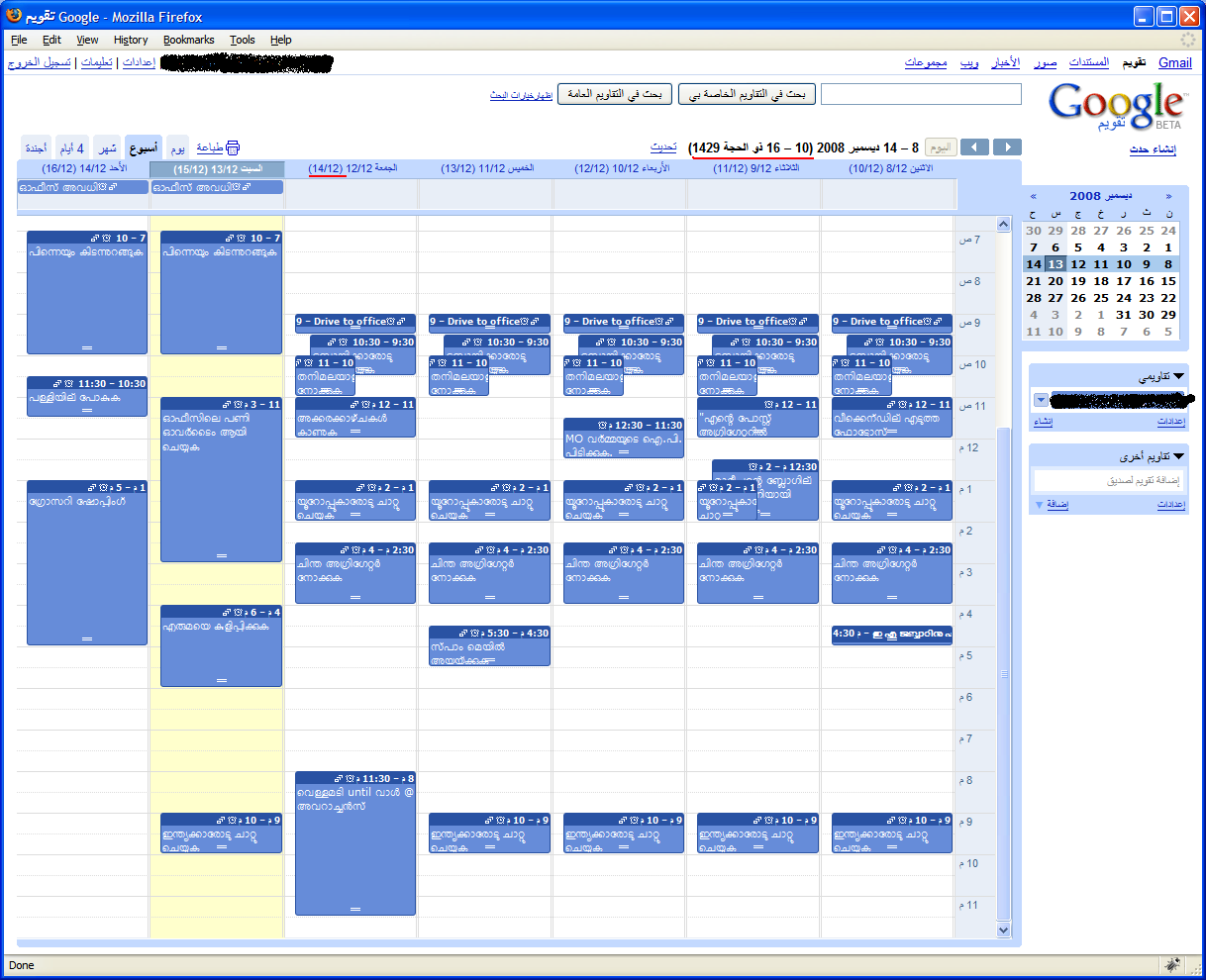
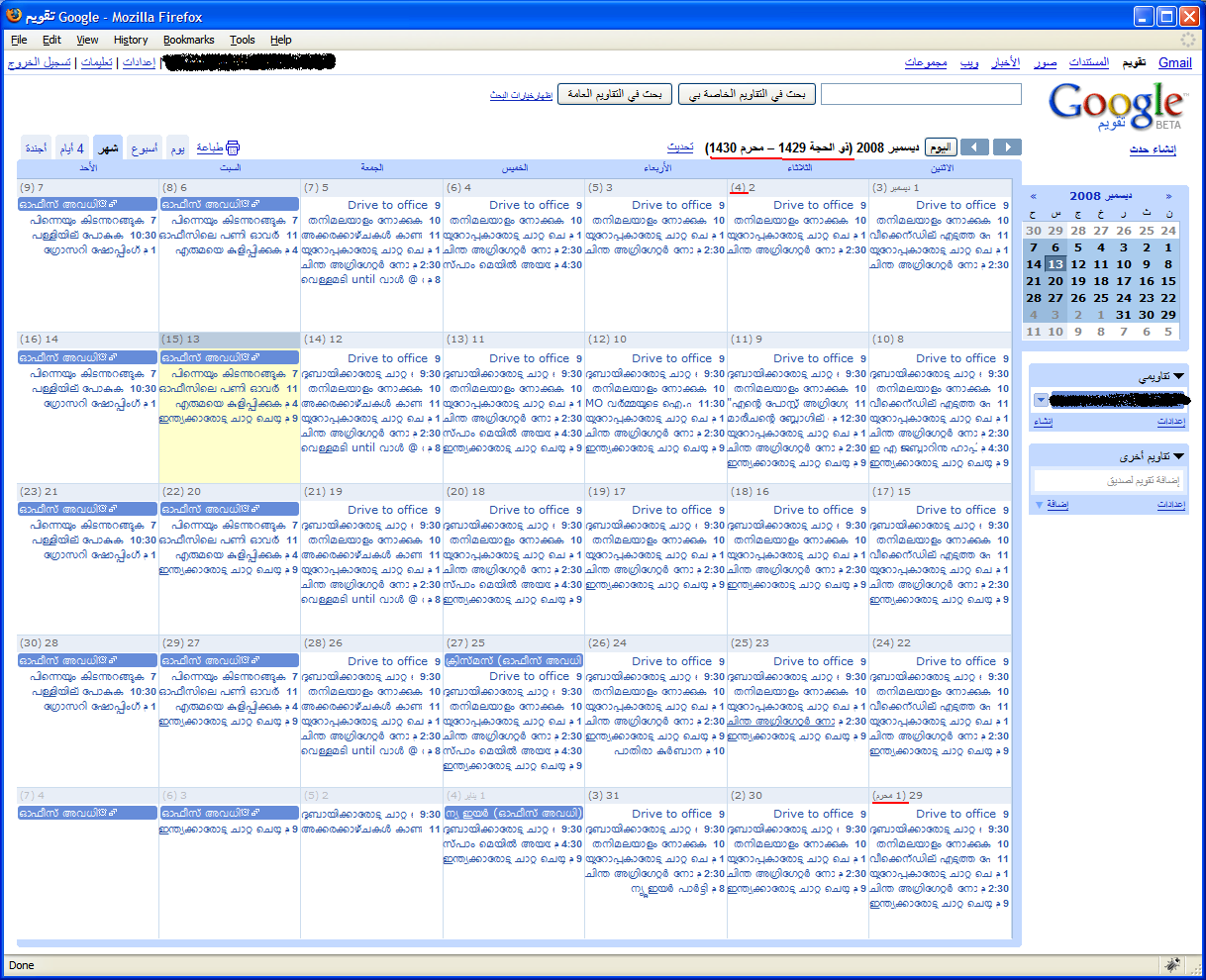
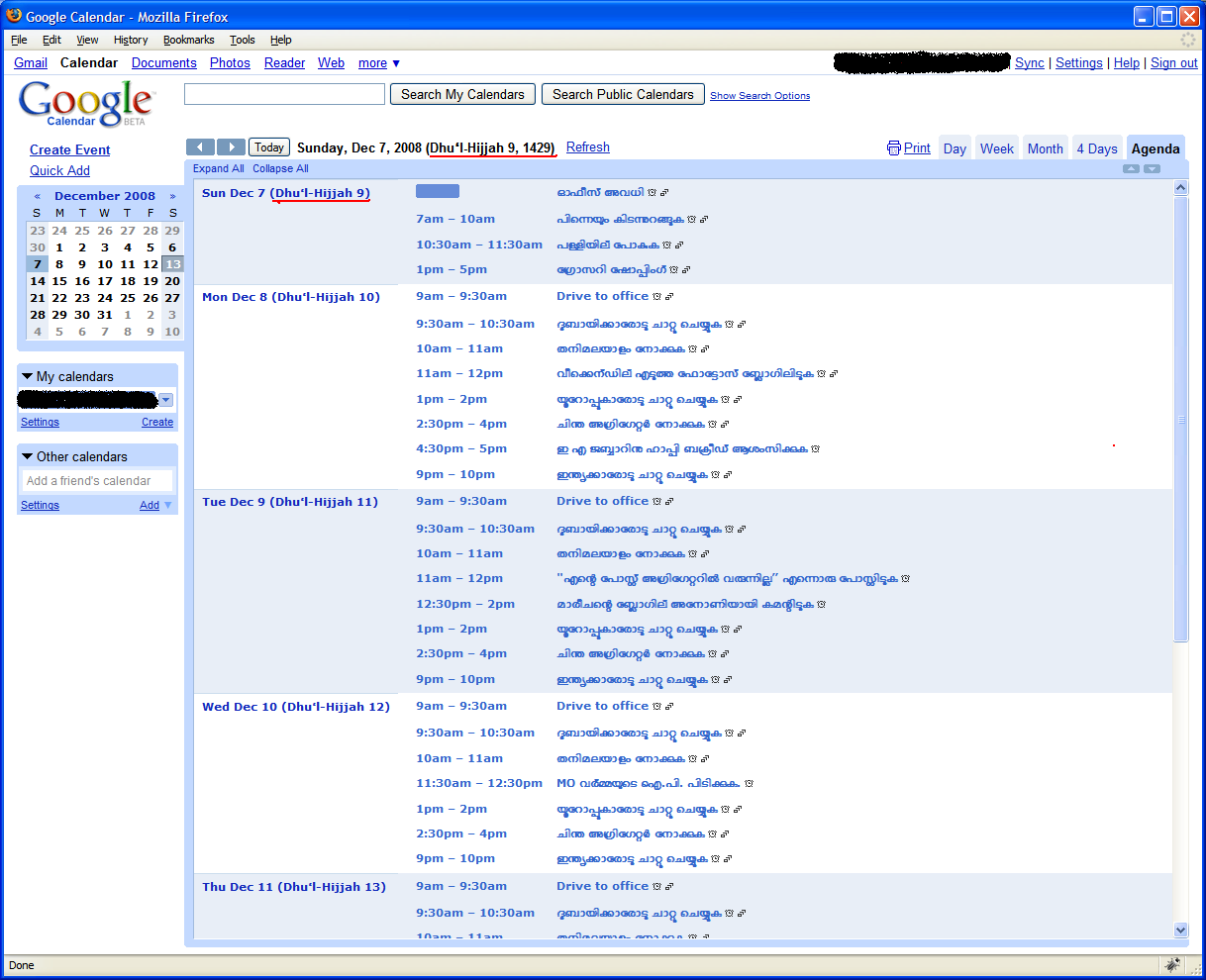
മയക്കം (ЛЕТАРГИЯ) [വാലന്റൈൻ ദിനം കഴിഞ്ഞുള്ളതു്]
അങ്ങനെ വേലായുധന്റെ ദിവസം കഴിഞ്ഞു. രാമസേനയിലെ വാനരന്മാർ എന്തു ചെയ്തു എന്നറിയില്ല. അവർക്കു കിട്ടിയ പിങ്കു നിറമുള്ള ഷഡ്ഡികൾക്കു് എന്തു പറ്റിയെന്നും അറിയില്ല.
കുഴൂർ വിത്സനും സന്തോഷും എഴുതിയ പ്രണയദിനകവിതകൾ വായിച്ചല്ലോ. ഇനി വാലന്റൈൻ ദിവസം കഴിഞ്ഞ സ്ഥിതിക്കു് നമുക്കു് പ്രണയം നഷ്ടമായവർക്കു വേണ്ടി ഒരു കവിത ചൊല്ലാം.
കാത്തിരിക്ക എന്ന മനോഹരകവിത എഴുതിയ റഷ്യൻ കവി കോൺസ്റ്റാന്റിൻ സിമോണോവിന്റെ മയക്കം (ЛЕТАРГИЯ) എന്ന കവിതയുടെ പരിഭാഷ വായിക്കൂ. (“ഓമനക്കുട്ടൻ ഗോവിന്ദൻ…” അല്ലെങ്കിൽ “ആരു വാങ്ങുമിന്നാരു വാങ്ങും…” എന്ന ഈണത്തിൽ വായിക്കുക.)
മയക്കം |
ЛЕТАРГИЯ |
|
|
|
|
കുഞ്ഞുനാളിലൊരിക്കലമ്മൂമ്മ ചൊന്നതാം കഥയാണിതു്: പണ്ടൊരിക്കൽ മയക്കമാർന്നൊരു കുഞ്ഞു, ജീവൻ വെടിഞ്ഞതായ് ചൊല്ലി സംസ്കരിച്ചത്രേ വീട്ടുകാർ; കല്ലറയ്ക്കുള്ളിൽ വെച്ചവൾ തൻ മയക്കത്തിൽ നിന്നുണർന്നു പോൽ, തൊണ്ട പൊട്ടിയലറി പോൽ. |
В детстве быль мне бабка рассказала Об ожившей девушке в гробу, Как она металась и рыдала, Проклиная страшную судьбу, |
|
ദീനരോദനം കേട്ട നാട്ടുകാ- രോടി വന്നു തുറക്കവേ പാവം കുഞ്ഞിൻ തുറിച്ച കണ്ണിലെ ഭീതി കണ്ടു പകച്ചു പോൽ. |
Как, услышав неземные звуки, Сняв с усопшей тяжкий гнет земли, Выраженье небывалой муки Люди на лице ее прочли. |
|
|
|
|
ഞാനൊരിക്കൽ പനി പിടിച്ചു ശ- യ്യാവലംബിയായൊട്ടു നാൾ കൂടെയെന്നമ്മ വന്നിരിക്കവേ ഏറെ ഭീതി തുളുമ്പിടും കൺകൾ ബദ്ധപ്പെട്ടൊന്നു പൊക്കി ഞാൻ ചൊന്നു ദീനസ്വരത്തൊടേ: “ഞാൻ മരിക്കുകിലെന്നെ നീയട- ക്കീടൊലാ, യിരു പത്തു നാൾ” |
И в жару, подняв глаза сухие, Мать свою я трепетно просил, Чтоб меня, спася от летаргии, Двадцать дней никто не хоронил. |
|
|
|
|
ഈ വിധത്തിൽത്താനല്ലേ നമ്മുടെ സ്നേഹത്തോടു ചെയ്യുന്നു നാം? ഓരോ രാവിലുമിഞ്ചിഞ്ചായതിൻ പ്രാണൻ പൊയ്ക്കൊണ്ടിരിക്കുന്നു; നമ്മളോടു സഹായിച്ചീടുവാൻ എന്നും യാചിച്ചു കേഴുന്നു; നിസ്സഹായരായ്, സ്തബ്ധമേധരായ്, നഷ്ടധൈര്യരായ് നില്പു നാം. |
Мы любовь свою сгубили сами, При смерти она, из ночи в ночь Просит пересохшими губами Ей помочь. А чем нам ей помочь? |
|
മാരി കോരിച്ചൊരിഞ്ഞിടും ശരത്- ക്കാലനാളൊരു രാവിലെ നമ്മുടെ സ്നേഹമേറെ നോവുമാ- യന്ത്യശ്വാസം വലിക്കവേ, പെട്ടിയൊന്നിലടച്ചു പൂട്ടി, മ- ണ്ണിട്ടു രണ്ടു കുടന്ന, പൂ വെച്ചു മേലെ കുരിശും, വീർപ്പൊന്നു വിട്ടു, തീർന്നു – മടങ്ങി നാം! |
Завтра отлетит от губ дыханье, А потом, осенним мокрым днем, Горсть земли ей бросив на прощанье, Крест на ней поставим и уйдем. |
|
ഒന്നു ചിന്തിക്ക, നമ്മുടെ പ്രേമ- മിന്നു മൊത്തം മരിച്ചുവോ? ഗാഢമാകും മയക്കമാർന്നതു ബോധമറ്റു കിടക്കയോ? പൊള്ളയായ വാക്കുള്ളു വിട്ടവ തള്ളി നാം ന്യായമോതവേ, (ഇത്തരം പണി ചെയ്വതിന്നു നാം എത്ര ചാതുര്യമാർന്നവർ?) തൻ മയക്കത്തിൽ നിന്നുണർന്നതു വൻ നിരാശതയാർന്നിടും ക്ഷീണശബ്ദത്തൊ, ടാഴും ദുഃഖത്തോ- ടോതുന്നോ ചില വാക്കുകൾ? |
Ну, а вдруг она, не как другие, Нас навеки бросить не смогла, Вдруг ее не смерть, а летаргия В мертвый мир обманом увела? Мы уже готовим оправданья, |
|
തീരെ വൈകുന്നതിന്നു മുമ്പു നാം വേഗം ശ്രദ്ധിക്ക, കേൾക്കുക: നമ്മുടെ തീവ്രപ്രേമം നിദ്ര വി- ട്ടിന്നു മൃത്യു വരിക്കവേ തന്റെ പ്രാണനെ രക്ഷ ചെയ്യുവാ- നുള്ള ദീനമാം പ്രാർത്ഥന… മൂടും മുമ്പിരു പത്തു നാൾകൾ കാ- ത്തീടണമെന്ന യാചന… |
Слушай же ее, пока не поздно, Слышишь ты, как хочет она жить, Как нас молит – трепетно и грозно – Двадцать дней ее не хоронить! |
|
|
|
പതിനെട്ടു കൊല്ലത്തിനു ശേഷമാണു് ഒരു റഷ്യൻ കവിത പരിഭാഷപ്പെടുത്തുന്നതു്. പണ്ടു പഠിച്ച റഷ്യനൊക്കെ മറന്നു പോയിരിക്കുന്നു. വാലന്റൈൻസ് ഡേയ്ക്കു വേണ്ടി ഒന്നു രണ്ടു റഷ്യൻ പ്രണയകവിതകൾ പരിഭാഷപ്പെടുത്താൻ ശ്രമിച്ചിട്ടു് ഒന്നും ശരിയായില്ല. അപ്പോഴാണു് ഇതു ശ്രമിച്ചതു്.
ഇരുപതു കൊല്ലം മുമ്പു് ഇതൊന്നു പരിഭാഷപ്പെടുത്താൻ ശ്രമിച്ചിരുന്നു. അതു നഷ്ടപ്പെട്ടു പോയി. അവസാനത്തേതൊഴികെ എല്ലാ പദ്യങ്ങളും വസന്തതിലകത്തിലായിരുന്നെന്നും അവസാനത്തേതു മാലിനിയിലായിരുന്നു എന്നും ഓർമ്മയുണ്ടു്. ഓർമ്മയുള്ള തുടക്കവും ഒടുക്കവും:
മുത്തശ്ശി ചൊന്ന കഥയാ; ണൊരു പെൺകിടാവു്,
നിദ്രാവിമുക്ത,….
…..
…..
ഇരുപതു ദിവസത്തേയ്ക്കെന്നെ മൂടായ്കയെന്നോ?
അതു നഷ്ടപ്പെട്ടു പോയതു് ഏതായാലും നന്നായി!