Gurukulam | ഗുരുകുലം

ഒരു കാലത്തെഴുതിയ കൃതികൾക്കു് പിൽക്കാലത്തു് അതിനോടു യാതൊരു ബന്ധവുമില്ലാത്ത ഒരു അർത്ഥം യാദൃച്ഛികമായി ഉണ്ടാവുന്നതു നിരീക്ഷിക്കുന്നതു രസാവഹമാണു്. ഹരിനാമകീർത്തനത്തിലെ “ഗർഭസ്ഥനായ് ഭുവി ജനിച്ചും മരിച്ചും…” എന്ന പദ്യത്തിലെ “ഉദകപ്പോള” എന്ന വാക്കിനെ “അപ്പോളോ” എന്നായി തെറ്റിദ്ധരിച്ചു് അമേരിക്ക ആകാശത്തേയ്ക്കു വിട്ട പേടകം എന്നർത്ഥം കൊടുത്തു് ആ പദ്യത്തിന്റെ അർത്ഥം മനസ്സിലാക്കിയതും, “അങ്കുശമില്ലാത്ത ചാപല്യമേ, മന്നിലംഗനയെന്നു വിളിക്കുന്നു നിന്നെ ഞാൻ” എന്ന ഈരടിയിലെ “അങ്കുശം” എന്ന വാക്കിനു് ചങ്ങമ്പുഴയുടെ കാലത്തു പ്രചാരത്തിലില്ലാത്ത അർദ്ധവിരാമം (comma) എന്ന അർത്ഥമെടുത്തു് അതിന്റെ ശരിയായ അർത്ഥത്തെക്കാളും സമഞ്ജസമായ ഒരു അർത്ഥം ഉണ്ടാക്കിയെടുത്തതും ഞാൻ അബദ്ധധാരണകൾ എന്ന പോസ്റ്റിൽ വിവരിച്ചിട്ടുണ്ടു്. ചരിത്രം എഴുതപ്പെടാത്ത കാലത്തെ സാഹിത്യകൃതികളെ വ്യാഖ്യാനിക്കുമ്പോൾ ഇങ്ങനെയുള്ള എത്രയെത്ര തെറ്റായ അർത്ഥങ്ങൾ ഉണ്ടാകുന്നെന്നു് ആർക്കറിയാം!

ഇതു് ഇപ്പോൾ എഴുതാൻ കാരണം കഴിഞ്ഞാഴ്ച കുറേ മലയാളിസുഹൃത്തുക്കളുമായി ഒത്തു ചേർന്നപ്പോഴുള്ള സംഭാഷണവും അതിൽ നിന്നു് എനിക്കു് ഒരു പഴയ ശ്ലോകത്തിനു് പുതിയ ഒരർത്ഥം തോന്നിയതുമാണു്.

ലോൿസഭാ തിരഞ്ഞെടുപ്പു നടക്കുന്ന സാഹചര്യത്തിൽ സ്വാഭാവികമായും മലയാളികളുടെ സൌഹൃദകൂടിക്കാഴ്ചകളിൽ തിരഞ്ഞെടുപ്പു തന്നെയായിരുന്നു മുഖ്യവിഷയം.

അമേരിക്കൻ മലയാളികളിൽ ഇടത്തുപക്ഷചിന്താഗതിയുള്ളവരെ മരുന്നിനു പോലും കാണാനില്ല. കോൺഗ്രസ്സാണോ ബി. ജെ. പി. യാണോ അതോ രണ്ടുമല്ലാത്ത അരാഷ്ട്രീയമാണോ എന്നു വ്യക്തമായി തിരിച്ചറിയാൻ കഴിയാത്ത ഒരു നിലപാടാണു പൊതുവേ. അഹിന്ദുക്കളിൽ നിന്നു പോലും ശ്രീരാമസേനയെപ്പോലുള്ള സംഭവങ്ങളെപ്പറ്റി അസഹിഷ്ണുത കണ്ടിട്ടില്ല. ചിരിച്ചുതള്ളാനുള്ള വാർത്തകൾ മാത്രമാണു് നാട്ടിൽ നടക്കുന്ന പല ദുഃഖകരമായ സംഭവങ്ങളും. നാട്ടിലെ ന്യൂനപക്ഷങ്ങളുടെ നേർക്കുള്ള അക്രമം ഒരു പ്രശ്നമല്ലെങ്കിലും അമേരിക്കയിൽ വടക്കേ ഇന്ത്യക്കാരും തെലുങ്കരും മലയാളികളെ പാര വെയ്ക്കുന്നതും വെള്ളക്കാർ നീഗ്രോകളോടു പോലും കാണിക്കാത്ത വിവേചനം ഇന്ത്യാക്കാരോടു ചില സന്ദർഭങ്ങളിൽ (ഉദാഹരണമായി ഒരു കാർ ആക്സിഡന്റ് വന്നാൽ അമേരിക്കക്കാരൻ പോലീസ് അമേരിക്കക്കാരന്റെ കൂടെ മാത്രമേ നിൽക്കുകയുള്ളത്രേ!) കാണിക്കാറുള്ളതും ഒക്കെ ദൈവം മനുഷ്യരെ തുല്യരായി സൃഷ്ടിച്ചെങ്കിലും മനുഷ്യൻ മനുഷ്യനോടു കാണിക്കുന്ന അധർമ്മത്തിന്റെ ഉദാഹരണങ്ങളായി ചർച്ച ചെയ്യപ്പെടാറുണ്ടു്.

ലോൿസഭാ തിരഞ്ഞെടുപ്പിനെപ്പറ്റിയുള്ള ചർച്ച അധികം കഴിയുന്നതിനു മുമ്പേ ശശി തരൂരിലെത്തി. ഇത്രയും കഴിവുള്ള ഒരു മനുഷ്യൻ പാർലമെന്റിൽ എത്തേണ്ടതു കേരളത്തിന്റെ ആവശ്യമാണെന്നും (ഒരു പാർലമെന്റംഗത്തിന്റെ അടിസ്ഥാനയോഗ്യത ഇംഗ്ലീഷും ഹിന്ദിയും നന്നായി കൈകാര്യം ചെയ്യാൻ അറിവുണ്ടായിരിക്കുക എന്നതാണെന്നും, മലയാളവും കേരളവും ജനസേവനവും രാഷ്ട്രീയപരിചയവും ഒന്നും പ്രശ്നമേ അല്ല എന്നും ഉള്ള അഭിപ്രായം കേരള ഫാർമർക്കു മാത്രമല്ല എന്നു മനസ്സിലായി. അല്ലെങ്കിലും, വിമാനം ഓടിച്ചു നടന്ന രാജീവ് ഗാന്ധിയെ പ്രധാനമന്ത്രിയാക്കിയവരാണല്ലോ നമ്മൾ!) അദ്ദേഹത്തെ ജയിപ്പിക്കാൻ മണ്ണിനോടു സ്നേഹമുള്ള മലയാളികൾ കഷിരാഷ്ട്രീയം നോക്കാതെ ഒന്നിച്ചു നിൽക്കണം എന്നും പരക്കെ അഭിപ്രായമുണ്ടായി. കേരളീയർ പൊതുവേ നിർഭാഗ്യവാന്മാരാണെന്നും നല്ല കഴിവുള്ള ആളുകൾ തിരഞ്ഞെടുപ്പിനു നിൽക്കുമ്പോൾ അവരെ ജയിപ്പിക്കാതെ പാർലമെന്റിൽ പെർഫോം ചെയ്യാൻ കഴിവില്ലാത്തവരെ ജയിപ്പിച്ചു വിടുന്നതു കൊണ്ടാണു നമുക്കു മന്ത്രിമാരെ കിട്ടാതെ കേരളത്തിന്റെ വികസനം മുരടിച്ചു പോകുന്നതെന്നും ഉള്ള അഭിപ്രായങ്ങൾ കേട്ടു. എന്തു പറഞ്ഞാലും കാര്യമില്ലാത്ത ഇടതന്മാരുടെ കാര്യം പോകട്ടേ, കോൺഗ്രസ്സും ബി. ജെ. പി. യും ഒന്നിച്ചു നിന്നു് ശശി തരൂരിനെ പാർലമെന്റിൽ എത്തിക്കാൻ ശ്രമിക്കും എന്നായിരുന്നു ആകെയുള്ള ഒരു പ്രതീക്ഷ.

ഇതു കേട്ടപ്പോൾ എനിക്കു് പഴയ ഒരു ശ്ലോകം ഓർമ്മ വന്നു. നീലകണ്ഠദീക്ഷിതരുടെ അന്യാപദേശശതകത്തിലെ “നാംഭോജായ ശശീ ന ചാപി ശശിനേ…” എന്ന ശ്ലോകത്തിനു് (ഈ ശ്ലോകം എത്ര ആലോചിച്ചിട്ടും കിട്ടുന്നില്ല. കയ്യിലുള്ള പുസ്തകങ്ങളിലും കാണുന്നില്ല. ആർക്കെങ്കിലും അറിയാമെങ്കിൽ ദയവായി പറഞ്ഞുതരൂ!) കേരളവർമ്മ വലിയകോയിത്തമ്പുരാന്റെ പരിഭാഷ. വൃത്തം കുസുമമഞ്ജരി.

പകൽ മാത്രം വിടരുന്ന താമര സൂര്യന്റെ ഭാര്യയാണെന്നും അവൾ ചന്ദ്രന്റെ ശത്രുവാണെന്നും ആണു് കവിസങ്കേതം. (ചന്ദ്രൻ പകലും ഉദിക്കും എന്നും പക്ഷേ സൂര്യന്റെ പ്രകാശത്തിൽ അസ്തപ്രജ്ഞനായി ഇരിക്കുകയാണെന്നും ഉള്ള ശാസ്ത്രസത്യം അവിടെ നിൽക്കട്ടേ.) അവർക്കു തമ്മിൽ യാതൊരു ഇടപാടുമില്ല. അതുകൊണ്ടു് രണ്ടു പേർക്കും ഒരു ചേതവുമില്ല. എങ്കിലും രണ്ടു കൂട്ടർക്കും വളരെയധികം സൌന്ദര്യമുണ്ടു് (അഭിരാമരാമവരു…). അവർ ചേരേണ്ടവർ തന്നെയാണു്. അങ്ങനെ ചേർന്നില്ലെങ്കിൽ അതു വിധിയുടെ പേരുദോഷം എന്നു മാത്രം പറഞ്ഞാൽ മതി. അവർ ചേർന്നിരുന്നെങ്കിൽ എന്നാണു കവിയുടെ ആഗ്രഹം എന്നർത്ഥം.

താമരയും ശശിയും തമ്മിലുള്ള ബന്ധത്തിന്റെ ആവശ്യകതയെപ്പറ്റി ഊന്നിപ്പറയുന്ന ഈ ശ്ലോകത്തിനു് യാദൃച്ഛികമായെങ്കിലും (ചന്ദ്രനു വേറേ പല പര്യായങ്ങളുണ്ടെങ്കിലും കുസുമമഞ്ജരി കേരളവർമ്മയെക്കൊണ്ടു് “ശശി” എന്നു തന്നെ എഴുതിച്ചല്ലോ!) ഇങ്ങനെയൊരു വ്യാഖ്യാനം ഉണ്ടാകാൻ സാധിക്കുന്നതു രസകരമാണു്. ഈ വിധത്തിൽ ആലോചിച്ചാൽ ഈ ശ്ലോകം ഇങ്ങനെ ആരെങ്കിലും മാറ്റിയെഴുതുന്നതാണു നല്ലതെന്നു തോന്നി.

ഇതെഴുതിക്കഴിഞ്ഞപ്പോഴാണു് തൊമ്മൻ കാണിച്ചു തന്ന (അമേരിക്കൻ മലയാളിക്കു ശശി തരൂരിനോടു് ഒരു ചായ്‌വുണ്ടെന്നു് തൊമ്മൻ പരോക്ഷമായി പറഞ്ഞുവെയ്ക്കുന്നുമുണ്ടു്) ഈ ലിങ്ക് കണ്ടതു്. അതുപോലെ ബി. ജെ. പി. ക്കു വോട്ടു ചെയ്യാനും, ശശി തരൂരിനെ ജയിപ്പിക്കാനും ഒരേ ബ്ലോഗ് തന്നെ ആഹ്വാനം ചെയ്യുന്നതും.

ഈ തെരഞ്ഞെടുപ്പുകാലത്തു് പലവിധ വിവാദങ്ങളിലായി മാധ്യമങ്ങള്‍ മുക്കിക്കളഞ്ഞ ചില സുപ്രധാന രാഷ്ട്രീയ വിഷയങ്ങള്‍ സ്വയം ഓര്‍ക്കാനും ഉറപ്പുവരുത്താനും :

• കമ്പോളമല്ല, ഗവണ്‍മെന്റാണു രാജ്യം ഭരിക്കേണ്ടതെന്നു പ്രഖ്യാപിക്കാൻ.
• ഭീകരതയ്ക്കു വിത്തുവിതയ്ക്കുന്ന വര്‍ഗ്ഗീയതയെ ചെറുക്കാൻ.
• ഇന്ത്യന്‍ പൊതുമേഖല ശക്തിപ്പെടുത്താൻ.
• 60% ജനങ്ങൾ ഉപജീവനമാര്‍ഗ്ഗം തേടുന്ന കാര്‍ഷിക മേഖലയിൽ ചെലവാക്കുന്ന തുകയുടെ പകുതി സര്‍ക്കാര്‍ സബ്സിഡി നല്‍കുമെന്നു പ്രഖ്യാപിക്കാൻ.
• വിദ്യാഭ്യാസം, ആരോഗ്യം, ഗതാഗതം, ജലം എന്നീ മേഖലകൾ സര്‍ക്കാര്‍ മേല്‍നോട്ടത്തിലും ഉടമസ്ഥതയിലും സംരക്ഷിക്കാൻ.
• പി.എഫ്. പലിശ നിരക്ക് 13% ആയി ഉയര്‍ത്തുകയും പി.എഫ് തുക സ്വകാര്യ കമ്പനികൾ വഴി ഓഹരികമ്പോളത്തിന് കൈമാറാനുള്ള യു.പി.എ. സര്‍ക്കാരിന്റെ തീരുമാനം പിന്‍വലിക്കുകയും ചെയ്യുമെന്നു് ഉറപ്പിക്കാൻ.
• പെന്‍ഷന്‍ സ്വകാര്യവല്‍ക്കരണബിൽ, ബാങ്കിംഗ് ബിൽ, ഇന്‍ഷൂറന്‍സ് വിദേശ നിക്ഷേപ പരിധി ഉയര്‍ത്താനുള്ള ബിൽ എന്നിവ പിന്‍വലിക്കാൻ.
• സര്‍ക്കാർ, അര്‍ദ്ധസര്‍ക്കാര്‍, സംസ്ഥാനസര്‍ക്കാര്‍ മേഖലകളിലും പൊതുമേഖലയിലും കഴിഞ്ഞ 15 വര്‍ഷമായി കാര്യമായി റിക്രൂട്ട്മെന്റ് നടക്കാത്തതുമൂലം ഒഴിഞ്ഞു കിടക്കുന്ന 50 ലക്ഷം വേക്കന്‍സികളിൽ ഉടന്‍ നിയമനം നടത്തുമെന്നു് ഉറപ്പുവരുത്താന്‍.
• ഇന്ത്യയുടെ പരമാധികാരവും സ്വാതന്ത്ര്യവും സാമ്പത്തിക മുന്‍ഗണനകളും തകര്‍ക്കുന്ന അന്താരാഷ്ട്ര കരാറുകളില്‍ നിന്നു പിന്മാറുമെന്നും പാര്‍ലമെന്റിന്റെ അനുമതിയില്ലാതെ അത്തരം കരാറുകളില്‍ ഇനി ഏര്‍പ്പെടില്ലന്നും ഉറപ്പുവരുത്താൻ.
• തൊഴില്‍ സുരക്ഷ ഉറപ്പുവരുത്താൻ, പണിമുടക്കാനും വിലപേശാനും തൊഴിലാളികൾക്കുള്ള അവകാശം സംരക്ഷിക്കാൻ.
• ഭൂപരിഷ്കരണം നടപ്പാക്കുവാനും സെസുകള്‍ക്കുവേണ്ടി അന്യായമായി കര്‍ഷകരുടെ ഭൂമി ഏറ്റെടുക്കില്ലെന്നു് ഉറപ്പുവരുത്താനും.
• കോര്‍പ്പറേറ്റ് നികുതി 50 ശതമാനമായി ഉയര്‍ത്താനും ഓഹരി കമ്പോളത്തിലെ ഇടപാടുകള്‍ക്ക് നികുതി ചുമത്താനുമുള്ള രാഷ്ട്രീയ ഇച്ഛാശക്തി കാട്ടാൻ.
• സംസ്ഥാനങ്ങളില്‍ നിന്ന് പിരിച്ചെടുക്കുന്ന കേന്ദ്രനികുതി വരുമാനം അതത് സംസ്ഥാനങ്ങള്‍ക്കുതന്നെ നല്‍കുമെന്ന് ഉറപ്പുനല്‍കാൻ.

(സ്ക്രിപ്റ്റ് അവലംബം: PAG ബുള്ളറ്റിൻ. പോസ്റ്റര്‍ ഡിസൈന്‍ : പരാജിതൻ)

നിയമപ്രകാരമുള്ള മുന്നറിയിപ്പു്: ഈ പോസ്റ്റു മുഴുവൻ കണക്കാണു്. (എന്റെ എല്ലാ പോസ്റ്റും കണക്കാണു്, അതു വേറെ കാര്യം.) ഈ പോസ്റ്റും അതിന്റെ കമന്റുകളും വായിച്ചെങ്കിലേ ഇതു മനസ്സിലാവൂ. അതു വായിക്കാൻ കരളുറപ്പില്ലാത്ത ദുർബ്ബലരും വിശാലരും ദയവായി ഈ പോസ്റ്റ് വായിച്ചോളൂ.

ബാബു കല്യാണത്തിനെക്കൊണ്ടു് ഒരു രക്ഷയുമില്ല. ഇതാ വേറൊരു സാധനവും കൊണ്ടു വന്നിരിക്കുന്നു…

അങ്ങേരു പറഞ്ഞതു ചുരുക്കി മലയാളത്തിലാക്കിയാൽ:

1. മൂന്നു റ്റൂ-ബെഡ്‌റൂം ഫ്ലാറ്റുകൾ.
   1. ഒരു വീട്ടിലെ രണ്ടു ബെഡ്‌റൂമുകളിൽ ഒന്നിൽ പെണ്ണു്, മറ്റേതിലും പെണ്ണു്.
   2. രണ്ടാമത്തെ വീട്ടിലെ രണ്ടു ബെഡ്‌റൂമുകളിൽ ഒന്നിൽ സിംഹം, മറ്റേതിലും സിംഹം.
   3. മൂന്നാമത്തെ വീട്ടിലെ രണ്ടു ബെഡ്‌റൂമുകളിൽ ഒന്നിൽ പെണ്ണു്, മറ്റേതിൽ സിംഹം.
   4. ഏതിൽ എന്തെന്നു് ബാബുവിനു് യാതൊരു പിടിയുമില്ല.
2. ആദ്യം ഫ്ലാറ്റ് തിരഞ്ഞെടുക്കണം.
3. പിന്നെ ഫ്ലാറ്റിലെ ഒരു ബെഡ്‌റൂം തിരഞ്ഞെടുക്കണം.
   1. അതിൽ സിംഹമാണെങ്കിൽ അപ്പോൾത്തന്നെ കഥ കഴിഞ്ഞു.
   2. അതിൽ പെണ്ണാണെങ്കിൽ…
      1. പെണ്ണാണെന്നു് കണ്ടതിനു ശേഷം അവൾ കതകടയ്ക്കും.
      2. എന്നിട്ടു് അവൾ ഒരു നാണയം ടോസ് ചെയ്യും. അതിൽ അശോകസ്തംഭം വന്നാൽ അങ്ങനെ തന്നെ നിൽക്കും. അക്കം വന്നാൽ അവൾ മറ്റേ മുറിയിൽ പോകും. എന്നിട്ടു് ആ മുറിയിലെ ആൾ (പെണ്ണോ സിംഹമോ) ആദ്യത്തെ മുറിയിൽ വരും.
      3. ബാബുവിനു് ഒന്നുകൂടി ബെഡ്‌റൂം തിരഞ്ഞെടുക്കാം. അതിൽ സിംഹമാണെങ്കിൽ ചത്തു. പെണ്ണാണെങ്കിൽ ബാബു കല്യാണം.
4. ഇതാണു സെറ്റപ്പു് എന്നല്ലാതെ കൂടുതൽ വിവരമൊന്നും ഈ ചങ്ങാതിയ്ക്കു് അറിയില്ലെങ്കിൽ അവനു് ഏതെങ്കിലും ഒരു പെണ്ണിനെ കല്യാണം ചെയ്തു് സുഖമായി ഇഞ്ചിഞ്ചായി മരിക്കാൻ എന്താണു സംഭാവ്യത?

ദാ എന്റെ അനാലിസിസ്:

1. രണ്ടു പെണ്ണുമുള്ള വീട്ടിൽ കയറാൻ സാദ്ധ്യത 1/3. അതിൽ കയറിയാൽ കല്യാണം ഉറപ്പു്. കല്യാണസാദ്ധ്യത 1/3 x 1 = 1/3. സിംഹസാദ്ധ്യത 1/3 x 0 = 0.
2. രണ്ടു സിംഹമുള്ള വീട്ടിൽ കയറാൻ സാദ്ധ്യത 1/3. അതിൽ കയറിയാൽ മരണം ഉറപ്പു്. സിംഹസാദ്ധ്യത 1/3 x 1 = 1/3. കല്യാണസാദ്ധ്യത 1/3 x 0 = 0.
3. പെണ്ണും സിംഹവുമുള്ള വീട്ടിൽ കയറാനുള്ള സാദ്ധ്യത 1/3. അതിൽ കയറിയാൽ…
   1. ആദ്യം സിംഹത്തെ കിട്ടാനുള്ള സാദ്ധ്യത 1/2. അപ്പോൾ സിംഹസാദ്ധ്യത 1/3 x 1/2 = 1/6. കല്യാണസാദ്ധ്യത = 0.
   2. ആദ്യം പെണ്ണിനെ കിട്ടാനുള്ള സാദ്ധ്യത 1/2. (മൊത്തം സാദ്ധ്യത = 1/3 x 1/2 = 1/6) അങ്ങനെ വന്നാൽ രണ്ടാം തവണ…
      1. സിംഹത്തെ കിട്ടാൻ സാദ്ധ്യത 1/2. സിംഹസാദ്ധ്യത = 1/6 x 1/2 = 1/12.
      2. പെണ്ണിനെ കിട്ടാൻ സാദ്ധ്യത 1/2. കല്യാണസാദ്ധ്യത = 1/6 x 1/2 = 1/12.

അപ്പോൾ, മൊത്തം കല്യാണസാദ്ധ്യത = 1/3 + 0 + 0 + 1/12 = 5/12 = 41.66666… %. മൊത്തം സിംഹസാദ്ധ്യത = 0 + 1/3 + 1/6 + 1/12 = 7/12 = 58.3333…%.

ബാബു കല്യാണം അവിടെയും നിർത്തിയില്ല. വേറൊരു സാധനവും കൊണ്ടു വന്നു. രാജാവു് ഒന്നുകൂടി കോയിൻ ടോസ്സു ചെയ്തത്രേ. രണ്ടു തവണ പെണ്ണിനെത്തന്നെ കിട്ടിയാലും ഒന്നുകൂടി ടോസ്സ് ചെയ്യണമത്രേ!

അതിനെന്താ? എത്ര വേണമെങ്കിലും ടോസ് ചെയ്തോളൂ.

മുകളിലുള്ള കണക്കനുസരിച്ചു് പെണ്ണും സിംഹവുമുള്ള വീടു കിട്ടിയിട്ടു് അവിടെ രണ്ടു തവണ പെണ്ണിനെ കിട്ടാനുള്ള സാദ്ധ്യത 1/12 ആണെന്നു കണ്ടു. അടുത്ത തവണ നാണയം ടോസ് ചെയ്യുമ്പോൾ പെണ്ണിനെ കിട്ടാനുള്ള സാദ്ധ്യത പിന്നെയും പകുതിയാകും. അതായതു് 1/24.

അപ്പോൾ മൂന്നു തവണ ടോസ് ചെയ്താലും അവസാനം പെണ്ണിനെ കിട്ടാനുള്ള സാദ്ധ്യത = 1/3 + 0 + 0 + 1/24 = 9/24 = 3/8 = 37.5%

ബാബുവിന്റെ ചോദ്യം വ്യക്തമായതു് ഈ കമന്റിലാണു്. ആദ്യത്തെ രണ്ടു ട്രയലിലും പെണ്ണിനെ കിട്ടിയതിനു ശേഷം, മൂന്നാമത്തെ ട്രയലിൽ പെണ്ണിനെ (മുമ്പു കിട്ടിയ പെണ്ണിനെ വേണമെന്നില്ല) കിട്ടാനുള്ള സാദ്ധ്യത എന്താണു്?

ഇതിനെ Conditional probability എന്നു പറയും. A, B എന്നു രണ്ടു സംഭവങ്ങളുടെ സാദ്ധ്യത യഥാക്രമം P(A), P(B) ആണെന്നിരിക്കട്ടേ. A സംഭവിച്ചു എന്നു് ഉറപ്പായതിനു ശേഷം B സംഭവിക്കാനുള്ള സാദ്ധ്യതയെ P(B/A) എന്നു വിളിച്ചാൽ

ഇവിടെ,

A = വീടു തിരഞ്ഞെടുത്തതിനു ശേഷം ആദ്യത്തെ രണ്ടു ട്രയലിലും പെണ്ണിനെ കിട്ടുന്ന സംഭവം. P(A) = 5/12.
B = മൂന്നു ട്രയലിലും പെണ്ണിനെ കിട്ടുന്ന സംഭവം. P(B) = 3/8.

അപ്പോൾ, P(B/A) = (3/8) / (5/12) = 9/10.

ഇതു് അല്പം അവിശ്വസനീയമായ കാര്യമാണു്. രണ്ടു തവണ പെണ്ണിനെ കിട്ടാൻ തന്നെ പാടാണു്. അതു കിട്ടിയാൽ കുറ്റവാളി രണ്ടു പെണ്ണുള്ള വീട്ടിലാവാനാണു കൂടുതൽ സാദ്ധ്യത എന്നും അതാണു് മൂന്നാമത്തേതും പെണ്ണാവാനുള്ള സാദ്ധ്യത ഇങ്ങനെ കൂടിയതെന്നും ചായക്കടയിലെ ഇന്റ്യൂഷൻ വെച്ചു പറയാം.

ഇത്രയൊക്കെ കഷ്ടപ്പെട്ടു ടൈപ്പു ചെയ്തപ്പോഴാണു് ഇതു വിശദീകരിക്കാൻ മറ്റൊരു സരളമായ വഴിയുണ്ടെന്നു കണ്ടതു്. (തല്ലല്ലേ, ഒന്നു വിരട്ടി വിട്ടാൽ മതി!)

ബാബുവിനു് മൂന്നു വീടുകളുണ്ടു്. ഓരോ വീട്ടിലും മൂന്നു തവണ രണ്ടിലൊന്നു തിരഞ്ഞെടുക്കണം. അതായതു്, ഓരോ വീട്ടിലും 2 x 2 x 2 = 8 സാദ്ധ്യതകൾ. അങ്ങനെ മൊത്തം 3 x 8 = 24 സാദ്ധ്യതകൾ. ഇതിൽ ഏതെങ്കിലും ഒന്നു മറ്റൊന്നിനെക്കാൾ മെച്ചമാണന്നു ബാബുവിനു് അറിയാത്തതിനാൽ ഇരുപത്തിനാലിൽ ഏതു സംഭവിക്കാനും ബാബുവിന്റെ സംഭാവ്യത തുല്യം.

ഇനി, രണ്ടു സിംഹത്തിന്റെ വീട്ടിൽ കയറുന്ന 8 സാദ്ധ്യതകളിൽ ബാബു കാഞ്ഞുപോകും. രണ്ടു പെണ്ണിന്റെ വീട്ടിൽ കയറുന്ന 8 സാദ്ധ്യതകളിൽ ബാബുവിനു കല്യാണവും സംഭവിക്കും.

സിംഹവും പെണ്ണുമുള്ള വീട്ടിലാണു് അല്പം കോമ്പ്ലിക്കേഷൻ. അതിലെ 8 സാദ്ധ്യതകൾ താഴെച്ചേർക്കുന്നു.

1. LLL
2. LLG
3. LGL
4. LGG
5. GLL
6. GLG
7. GGL
8. GGG

ഇവയിൽ മൂന്നു ട്രയലിലും പെണ്ണാകാനുള്ള സാദ്ധ്യത (8) മാത്രം. അതായതു് ഒരു സാദ്ധ്യത മാത്രം. എന്നു വെച്ചാൽ 24 സാദ്ധ്യതകളിൽ 8+1 = 9 എണ്ണം മാത്രമേ മൂന്നു ട്രയലിനു ശേഷം ബാബുവിനു കല്യാണം കൊടുക്കൂ. 9/24 = 3/8 എന്നതു നമുക്കു മുകളിൽ കിട്ടിയ ഉത്തരം തന്നെ.

ഇനി, ആദ്യത്തെ രണ്ടു ട്രയലിൽ പെണ്ണാകാനുള്ള സാദ്ധ്യത: മുകളിലെ പട്ടികയിൽ (7), (8) എന്നിവ മാത്രം. അതായതു് 24-ൽ 8+2 = 10 സാദ്ധ്യതകൾ. അതിനാൽ ആദ്യത്തെ രണ്ടു ട്രയലിനു ശേഷം ബാബുവിനു കല്യാണത്തിനുള്ള സാദ്ധ്യത 10/24 = 5/12. ഇതും മുകളിൽ കണ്ടുപിടിച്ചതു തന്നെ.

10 സാദ്ധ്യതകളിൽ ആദ്യത്തെ രണ്ടെണ്ണം പെണ്ണാവുകയും, അവയിൽ ഒമ്പതെണ്ണത്തിൽ മൂന്നാമതും പെണ്ണാവുകയും ചെയ്യുന്നതുകൊണ്ടു്, ബാബുവിന്റെ അവസാനത്തെ ചോദ്യത്തിന്റെ ഉത്തരം 9/10.

പ്രോബബിളിറ്റി പ്രശ്നങ്ങൾ സോൾവു ചെയ്യുമ്പോൾ എനിക്കു ശരിയുത്തരം കിട്ടുന്നതിന്റെ പ്രോബബിളിറ്റി സാധാരണയായി വളരെ കുറവാണു്. അതുകൊണ്ടു് ഞാൻ എപ്പോഴും ഒരു സിമുലേഷൻ നടത്തി നോക്കും. ഇവിടെയും അതു ചെയ്തു. ഈ സംഭവം പത്തുലക്ഷം തവണ ചെയ്യുന്ന ഒരു കമ്പ്യൂട്ടർ പ്രോഗ്രാം എഴുതി ഓരോന്നും സംഭവിക്കുന്നതു് എണ്ണി. ഫലം താഴെ. (അതു രണ്ടു തവണ ചെയ്തു് ഉത്തരം ഒന്നു തന്നെ കിട്ടുമോ എന്നു പരിശോധിച്ചതാണു് ഇടത്തും വലത്തും.)

$ monty.py
Total trials =  1000000

First House = 334205 = 33.4205 %
Second House = 332556 = 33.2556 %
Third House = 333239 = 33.3239 %

Lion in First house = 334205 = 33.4205 %
Lion in Third house = 166628 = 16.6628 %
Girl and Lion in Third house = 83563 = 8.3563 %
Girl, Girl and Lion in Third house = 41430 = 4.143 %

Lion in one trial = 500833 = 50.0833 %
Lion in two trials = 417768 = 41.7768 %
Lion in three trials = 375635 = 37.5635 %

Lion in one trial = 500833 = 50.0833 %
Lion in one or two trials = 584396 = 58.4396 %
Lion in one, two or three trials = 625826 = 62.5826 %

Girls in second house = 332556 = 33.2556 %
Girl in third house = 166611 = 16.6611 %
Girl and Girl in third house = 83048 = 8.3048 %
Girl, Girl and Girl in third house = 41618 = 4.1618 %

Girl in at least one trial = 499167 = 49.9167 %
Girls in at least two trials = 415604 = 41.5604 %
Girls in three trials = 374174 = 37.4174 %

$ monty.py
Total trials =  1000000

First House = 333400 = 33.34 %
Second House = 332692 = 33.2692 %
Third House = 333908 = 33.3908 %

Lion in First house = 333400 = 33.34 %
Lion in Third house = 167200 = 16.72 %
Girl and Lion in Third house = 83389 = 8.3389 %
Girl, Girl and Lion in Third house = 41446 = 4.1446 %

Lion in one trial = 500600 = 50.06 %
Lion in two trials = 416789 = 41.6789 %
Lion in three trials = 374846 = 37.4846 %

Lion in one trial = 500600 = 50.06 %
Lion in one or two trials = 583989 = 58.3989 %
Lion in one, two or three trials = 625435 = 62.5435 %

Girls in second house = 332692 = 33.2692 %
Girl in third house = 166708 = 16.6708 %
Girl and Girl in third house = 83319 = 8.3319 %
Girl, Girl and Girl in third house = 41873 = 4.1873 %

Girl in at least one trial = 499400 = 49.94 %
Girls in at least two trials = 416011 = 41.6011 %
Girls in three trials = 374565 = 37.4565 %

ഇതിലെ അവസാനത്തെ രണ്ടു വരികളാണു നോക്കേണ്ടതു്. (ഇടത്തു വശത്തെ ഫലമാണു് താഴെ ഉപയോഗിക്കുന്നതു്.) 1000000 തവണ ചെയ്തപ്പോൾ 415604 തവണ രണ്ടാമതും പെണ്ണിനെ കിട്ടി. 374174 തവണ മൂന്നാമതും പെണ്ണിനെ കിട്ടി.

അപ്പോൾ

• രണ്ടു ട്രയലിലും പെണ്ണിനെ കിട്ടാൻ സാ‍ദ്ധ്യത = 41.5%. മുകളിലെ കണക്കനുസരിച്ചു് സാദ്ധ്യത = 5/12 = 41.67%.
• മൂന്നു ട്രയലിലും പെണ്ണിനെ കിട്ടാൻ സാദ്ധ്യത = 37.4%. മുകളിലെ കണക്കനുസരിച്ചു് സാദ്ധ്യത = 3/8 = 37.5%.
• രണ്ടു തവണ പെണ്ണിനെ കിട്ടിയതിനു ശേഷം മൂന്നാമതും പെണ്ണിനെ കിട്ടാനുള്ള സാദ്ധ്യത = 374174/415604 = 0.9003 = 90.03%. മുകളിലെ കണക്കനുസരിച്ചു് സാദ്ധ്യത = 9/10 = 90%.

എല്ലാം കഴിഞ്ഞപ്പോഴാണു്, ഉണ്ടിരുന്ന ജോഷിക്കു് ഒരു വിളി തോന്നിയതു്.

ആദ്യം കതകു തുറന്ന പെണ്ണിനോടു് ബാബുവിനു് ഒരു സോഫ്റ്റ് കോർണർ ഉണ്ടായത്രേ! അവളെത്തന്നെ അവസാനവും കിട്ടാൻ സാദ്ധ്യത എന്താണു് എന്നറിയണം.

ഇരുപത്തിനാലു സാദ്ധ്യതകൾ ഉണ്ടെന്നു നാം മുകളിൽ കണ്ടു. അതിൽ സിംഹങ്ങൾ മാത്രമുള്ള എട്ടു സാദ്ധ്യതകൾ വിടുക. സിംഹവും പെണ്ണുമുള്ള എട്ടെണ്ണത്തിൽ ഒന്നിൽ അവസാനം പെണ്ണിനെ കിട്ടുമെന്നു കണ്ടു. അതു് ആദ്യത്തെ പെണ്ണാകാനേ വഴിയുള്ളൂ. അപ്പോൾ ഒരു സാദ്ധ്യത അവിടെ.

പെണ്ണും പെണ്ണുമുള്ള വീടു് ആയാലോ? നമുക്കു് പെണ്ണുങ്ങളെ ഗൌരി എന്നും ലിസി എന്നും വിളിക്കാം. എന്നിട്ടു മുകളിലെ പട്ടിക ഒന്നു കടമെടുക്കാം.

1. LLL
2. LLG
3. LGL
4. LGG
5. GLL
6. GLG
7. GGL
8. GGG

ആദ്യവും അവസാനവും ഒരേ പെണ്ണു വരാനുള്ള സാദ്ധ്യതകൾ (1), (3), (6), (8). അതായതു നാലു സാദ്ധ്യതകൾ. മൊത്തം 0 + 1 + 4 = 5 സാദ്ധ്യതകൾ. അതായതു് ആദ്യം പെണ്ണിനെ കിട്ടുകയും അവളെത്തന്നെ അവസാനവും കിട്ടുകയും ചെയ്യാനുള്ള സംഭാവ്യത 5/24.

ഇനി, രണ്ടു ട്രയലിൽ ഒരേ പെണ്ണു തന്നെ കിട്ടാനുള്ള സാദ്ധ്യതയോ? സിംഹ-സിംഹ-വീട്ടിൽ 0, സിംഹ-പെണ്ണു് വീട്ടിൽ 2, പെണ്ണു്-പെണ്ണു് വീട്ടിൽ (1), (2), (7), (8) എന്നു 4. മൊത്തം 0 + 2 + 4 = 6. സംഭാവ്യത = 6/24 = 1/4.

ജോഷിക്കു സമാധാനമായോ?

തർക്കമില്ലാത്ത പ്രോബബിലിറ്റി പ്രശ്നങ്ങളില്ല. നമുക്കു തർക്കിക്കാം. തർക്കിച്ചു തർക്കിച്ചു പോകാം…

വെള്ളെഴുത്തിന്റെ കർമ്മണിപ്രയോഗം എന്ന പോസ്റ്റിൽ ഇട്ട കമന്റിൽ ബാബുകല്യാണം (ഇവനെയൊന്നും കല്യാണം കഴിപ്പിച്ചു വിടാൻ ആരുമില്ലേ?) ചോദിച്ച ചോദ്യത്തിനു് ശ്രീഹരിയും (ഇവിടെയും ഇവിടെയും ഇവിടെയും)മധുസൂദനൻ പേരടിയും (ഇവിടെയും ഇവിടെയും ഇവിടെയും) തമ്മിൽ നടന്ന തർക്കത്തിനു മേൽ എന്റെ അഭിപ്രായമാണു താഴെ:

ശ്രീഹരിയുടെയും മധുസൂദനന്റെയും വാദങ്ങൾ മുഴുവനും വായിച്ചില്ല. എങ്കിലും, ശ്രീഹരിയാണു ശരിയെന്നു തോന്നുന്നു.

ഞാൻ മനസ്സിലാക്കിയിടത്തോളം ബാബു കല്യാണത്തിന്റെ പ്രശ്നം ഇങ്ങനെയാണു്:

1. രണ്ടു സിംഹവും രണ്ടു പെണ്ണും.
2. രാജാവു് നാണയം ടോസ്സ് ചെയ്യുന്നു. അശോകസ്തംഭം വന്നാൽ ആദ്യത്തെ മുറിയിൽ സിംഹത്തെ കയറ്റുന്നു. അക്കം വന്നാൽ പെണ്ണിനെയും.
3. രാജാവു വീണ്ടും നാണയം ടോസ്സ് ചെയ്യുന്നു. അശോകസ്തംഭം വന്നാൽ രണ്ടാമത്തെ മുറിയിൽ സിംഹത്തെ കയറ്റുന്നു. അക്കം വന്നാൽ പെണ്ണിനെയും.
4. തടവുകാരൻ ഒരു മുറി തുറന്നു് അകത്തു കയറുന്നു. ഏതു മുറിയിൽ എന്താണെന്നു് അവനു് അറിയില്ല. കയറുന്ന സ്ഥലത്തു് സിംഹമാണെങ്കിൽ ഉടനേ സുഖമായി മരിക്കുന്നു. പെണ്ണാണെങ്കിൽ അവളെ കല്യാണം കഴിച്ചു് വളരെക്കാലം കൊണ്ടു് ഇഞ്ചിഞ്ചായി വേദനയനുഭവിച്ചു മരിക്കുന്നു.

അവനു് സിംഹത്തിന്റെ വായിൽ‌പ്പെട്ടു മരിക്കാതെ പെണ്ണിനെക്കെട്ടി ജീവിക്കാനുള്ള സാദ്ധ്യതയാണു കണ്ടുപിടിക്കേണ്ടതു്.

ഇനി, താഴെപ്പറയുന്ന കാര്യങ്ങൾ കൂടി ശരിയാണെന്നും നമുക്കു് അനുമാനിക്കാം.

• നാണയത്തിന്റെ ഒരു വശത്തു് അശോകസ്തംഭവും മറ്റേ വശത്തു് അക്കവും ആകണം. അല്ലാതെ രണ്ടിലും സ്തംഭം വരരുതു്. ഒരിടത്തു് അശോകസ്തംഭവും അക്കവും കൂടിയും മറ്റേ വശത്തു കുടുംബാസൂത്രണത്തിന്റെ ചിഹ്നവും ഉള്ള നാണയം പാടില്ല.
• അശോകസ്തംഭവും അക്കവും വീഴാനുള്ള സാദ്ധ്യത തുല്യമായിരിക്കണം. നാണയം unbiased ആയിരിക്കണം എന്നർത്ഥം.
• കുറ്റവാളിക്കു യാതൊരു സൂചനയും ഇല്ല. അതിനാൽ അയാൾ ഒരു മുറി തിരഞ്ഞെടുക്കുന്നതും നാണയം ടോസ്സ് ചെയ്യുന്നതു പോലെ തന്നെ. 50%-50% സാ‍ദ്ധ്യത.

ഈ പ്രശ്നത്തെ രണ്ടു തരത്തിൽ കാണാം.

1. മേൽ‌പ്പറഞ്ഞ പ്രശ്നം നമുക്കു തന്നിട്ടു് ഉത്തരം കണ്ടുപിടിക്കാൻ പറയുക.
2. രാജാവു് നാണയം ടോസ്സ് ചെയ്തു് രണ്ടു മുറിയും നിറച്ചതിനു ശേഷം ഉത്തരം കണ്ടുപിടിക്കാൻ പറയുക.

രണ്ടിലും ഉത്തരം രണ്ടാണു്.

രണ്ടാമത്തേതു് ആദ്യം എടുക്കാം. രാജാവ് നാണയമിട്ടപ്പോൾ രണ്ടു തവണയും അശോകസ്തംഭം വന്നെന്നിരിക്കട്ടേ. രണ്ടിലും സിംഹങ്ങൾ. ഇവിടെ പ്രതി സിംഹത്തിന്റെ വായിൽ അകപ്പെടാനുള്ള സാദ്ധ്യത 100% ആണു്. നേരെ മറിച്ചു്, രണ്ടിലും അക്കം വരുകയും രണ്ടിലും പെണ്ണുങ്ങൾ ആവുകയും ചെയ്താൽ അതു 0% ആണു്. ഇനി ഒരെണ്ണം അശോകസ്തംഭവും മറ്റേതു് അക്കവും ആയി ഒന്നിൽ സിംഹവും മറ്റേതിൽ പെണ്ണുമായാൽ സിംഹമുള്ള വാതിൽ അയാൾ തിരഞ്ഞെടുക്കാൻ സാദ്ധ്യത 50% ആണു്.

രാജാവിന്റെ കോയിൻ ടോസ്സ് അനുസരിച്ചു് ഫലം മാറാം എന്നർത്ഥം.

ഇനി, ആദ്യത്തെ ചോദ്യം പരിശോധിക്കാം.

ഇതിൽ മൂന്നുതരം സംഭവങ്ങളുണ്ടു്.

ഒന്നാം സംഭവം: കുറ്റവാളി തിരഞ്ഞെടുക്കുന്ന വാതിൽ

സൂചനയൊന്നും ഇല്ലാത്തതിനാൽ ആദ്യത്തേയോ രണ്ടാമത്തെയോ വാതിൽ തിരഞ്ഞെടുക്കാനുള്ള സാദ്ധ്യത 1/2 വീതം.

രണ്ടാം സംഭവം: നാണയമിടുന്നതും സിംഹത്തെയോ പെണ്ണിനെയോ മുറിയിൽ ഇടുന്നതും.

ഒരു പോലെ സാദ്ധ്യതയുള്ള നാലു് സംഭവങ്ങളാണു് രാജാവു നാണയം ടോസ്സ് ചെയ്യുമ്പോൾ ഉണ്ടാവുക.

1. രണ്ടും അശോകസ്തംഭം. രണ്ടിലും സിംഹം.
2. രണ്ടും അക്കം. രണ്ടിലും പെൺ‌കുട്ടികൾ.
3. ആദ്യം അശോകസ്തംഭം, പിന്നെ അക്കം. ആദ്യത്തേതിൽ സിംഹം, രണ്ടാമത്തേതിൽ പെണ്ണു്.
4. ആദ്യം അക്കം, പിന്നെ അശോകസ്തംഭം. ആദ്യത്തേതിൽ പെണ്ണു്, രണ്ടാമത്തേതിൽ സിംഹം.

ഇവ നാലിനും സാദ്ധ്യത തുല്യം. 1/4 വീതം.

മൂന്നാം സംഭവം (ക): സിംഹമുള്ള മുറിയിൽ അകപ്പെട്ടാൽ സിംഹത്തിന്റെ വായിൽ പെട്ടു മരിക്കാനുള്ള സാദ്ധ്യത

സിംഹത്തിനു വെള്ളെഴുത്തോ വയറ്റുനോവോ ഇല്ലെന്നു കരുതിയാൽ ഇതു് നൂറു ശതമാനം ആണു്. 1 എന്നർത്ഥം.

മൂന്നാം സംഭവം (ഖ): പെണ്ണുള്ള മുറിയിൽ അകപ്പെട്ടാൽ സിംഹത്തിന്റെ വായിൽ പെട്ടു മരിക്കാനുള്ള സാദ്ധ്യത

ഇതു് പൂജ്യം ആണു്. കൂടുതൽ വേദനാജനകമായ മരണം അവനെ കാത്തിരിക്കുന്നു.

ഈ മൂന്നു സംഭവങ്ങളും തമ്മിൽ ബന്ധമില്ലാത്തതും ഒരേ സമയം സംഭവിക്കുന്നവയും ആകുന്നതു കൊണ്ടു് അവയുടെ സംഭാവ്യതകളെ തമ്മിൽ ഗുണിക്കുന്നു. അങ്ങനെ കിട്ടുന്ന സാദ്ധ്യതകളെ തമ്മിൽ കൂട്ടി മൊത്തം സാദ്ധ്യത കണ്ടു പിടിക്കുന്നു.

അപ്പോൾ സിംഹത്തിന്റെ വായിൽ അകപ്പെടാനുള്ള സാദ്ധ്യത

= (1/2 x 1/4 x 1 + 1/2 x 1/4 x 1) + (1/2 x 1/4 x 0 + 1/2 x 1/4 x 0) + (1/2 x 1/4 x 1 + 1/2 x 1/4 x 0) + (1/2 x 1/4 x 0 + 1/2 x 1/4 x 1)
= 1/4 + 0 + 1/8 + 1/8 = 1/2.

അതായതു്, കുറ്റവാളി സിംഹത്തിന്റെ വായിലകപ്പെടാനുള്ള സാദ്ധ്യത നേർപകുതി (50%) ആണു്.

സംഭാവ്യതാശാസ്ത്രത്തിലെ പല പ്രശ്നങ്ങളുടെയും ഉത്തരങ്ങളും ഇതുപോലെ ശരിയായി കണക്കുകൂട്ടിയാലേ കിട്ടൂ. സാഹചര്യമനുസരിച്ചു് അതു മാറുകയും ചെയ്യും. മധുസൂദനൻ പേരടി പറയുന്നതു പോലെ ചായക്കടയിലെ ഇന്റ്യൂഷനുമായി പോയാൽ പലപ്പോഴും തെറ്റായ ഉത്തരമേ കിട്ടൂ.

ഈ തരത്തിലുള്ള മറ്റൊരു പ്രശസ്ത പ്രശ്നമുണ്ടു് – മോണ്ടി ഹാൾ പ്രശ്നം. ഇതിൽ മൂന്നു വാതിലും ഒരു പെണ്ണും രണ്ടു സിഹവും ഉണ്ടു്. രാജാവു നാണയമൊന്നും ടോസ്സ് ചെയ്യുന്നില്ല. പകരം ഒരു വാതിലിനു പിന്നിൽ പെണ്ണിനെയും മറ്റു രണ്ടു വാതിലുകളുടെയും പിറകിൽ സിംഹങ്ങളെയും നിർത്തിയിരിക്കുന്നു. എന്നിട്ടു് കുറ്റവാളിയോടു് ഒരു വാതിൽ തിരഞ്ഞെടുക്കാൻ പറയും. അയാൾ ഏതു വാതിൽ തിരഞ്ഞെടുത്താലും സിംഹമുള്ള വേറേ ഒരു മുറിയെങ്കിലും ഉണ്ടായിരിക്കുമല്ലോ. ആ മുറിയുടെ കിളിവാതിൽ തുറന്നിട്ടു് അതിനകത്തു സിംഹമാണെന്നു് കുറ്റവാളിയെ കാണിക്കും. എന്നിട്ടു് കുറ്റവാളിക്കു് തന്റെ തീരുമാനം പുനഃപരിശോധിക്കാൻ അവസരം കൊടുക്കും. ഒന്നുകിൽ അയാൾക്കു് ആദ്യത്തെ വാതിൽ തന്നെ തുറക്കാം. അല്ലെങ്കിൽ അയാൾക്കു് സിംഹത്തെ കണ്ടതല്ലാത്ത മൂന്നാമത്തെ വാതിൽ തുറക്കാം. ഏതു തുറക്കുന്നതാണു് നല്ലതു്?

ഇതു വളരെയധികം തർക്കമുണ്ടാക്കിയിട്ടുള്ള ഒരു പ്രശ്നമാണു്. ഒരിക്കൽ ഈ ചോദ്യത്തിനു് മറിലിൻ സാവന്ത് പറഞ്ഞ ഉത്തരം തെറ്റാണെന്നു പറഞ്ഞു് പല ഗണിതശാസ്ത്രപ്രൊഫസർ മാർ വരെ ബഹളമുണ്ടാക്കിയായിരുന്നു. (മറിലിൻ പറഞ്ഞതു ശരിയായിരുന്നു.)

മൂന്നാമത്തെ വാതിൽ തുറക്കുന്നതാണു നല്ലതു്. കാരണം, ഓരോ വാതിലിലും പെണ്ണുണ്ടാകാനുള്ള സാദ്ധ്യത തുല്യമാണു് – 1/3 വീതം. ആദ്യത്തെ വാതിൽ തിരഞ്ഞെടുത്തപ്പോൾ അതിൽ പെണ്ണുണ്ടാകാനുള്ള സാദ്ധ്യത 1/3 ആയിരുന്നു. മറ്റു രണ്ടെണ്ണത്തിനും 2/3-ഉം. മറ്റു രണ്ടെണ്ണത്തിലെ സിംഹമുള്ള ഒരു വാതിൽ ഒഴിവാക്കിയാൽ മൂന്നാമത്തെ വാതിലിൽ പെണ്ണുണ്ടാകാനുള്ള സാദ്ധ്യത അതിനാൽ 2/3 ആണു്. അതായതു് തീരുമാനം മാറ്റിയാൽ സാദ്ധ്യത ഇരട്ടിയാകും എന്നർത്ഥം.

തർക്കിക്കുന്നവർക്കു രണ്ടു വാദങ്ങളാണു്:

1. ഓരോ വാതിലിന്റെയും സാദ്ധ്യത 1/3 ആണു്. ഒരു വാതിൽ സിംഹമാണന്നറിഞ്ഞാലും മറ്റു രണ്ടിലെയും സാദ്ധ്യതകൾ മാറുന്നില്ല. മാറിയാലും അവ 1/2 വീതമായിരിക്കും.

   ഇതു തെറ്റാണു്.

2. സിംഹത്തെ കാണുന്നതിനു മുമ്പു് എല്ലാ വാതിലിന്റെയും സാദ്ധ്യത 1/3 ആയിരുന്നു. സിംഹത്തെ കണ്ടുകഴിഞ്ഞു് ആദ്യത്തെ വാതിലിന്റെ സംഭാവ്യത മാറുന്നില്ലെങ്കിലും മൂന്നാമത്തെ വാതിലിന്റെ സാദ്ധ്യത 1/3-ൽ നിന്നു് 1/2 ആയി ഉയർന്നു.

   ഇതിലും മൂന്നാമത്തെ വാതിൽ തുറക്കുന്നതു തന്നെയാണു നല്ലതെന്നു പറയുന്നു എങ്കിലും കാരണം തെറ്റാണു്.

കൂടുതൽ വിവരങ്ങൾക്കു് വിക്കി ലേഖനം തന്നെ വായിക്കൂ. അതിന്റെ വിശദമായ വിശകലനവും തിയറിയും അതു പോലെയുള്ള മറ്റു പ്രശ്നങ്ങളിലേക്കുമുള്ള ലിങ്കും ഒക്കെയായി ഒരു ദിവസത്തെ വായനയ്ക്കുണ്ടു്.

സൂക്ഷിച്ചു കൈകാര്യം ചെയ്യേണ്ട ഒരു ഗണിതശാഖയാണു് സംഭാവ്യതാശാസ്ത്രം (Theory of Probability). അതിന്റെ ബേസിക് അസമ്‌പ്ഷൻസ് വിട്ടു പോകുന്നതാണു് പലപ്പോഴും തെറ്റു പറ്റാൻ കാരണം. അതുപോലെ നമുക്കു് അറിവുള്ള കാര്യങ്ങൾ മാറുമ്പോൾ സംഭാവ്യതയും മാറും. മുകളിൽ പറഞ്ഞ മോണ്ടി ഹാൾ പ്രശ്നം ഒരുദാഹരണം.

ഇതു പോലെ മറ്റൊരു പ്രഹേളികയുള്ളതു് ഒരു കഥയായി താഴെച്ചേർക്കുന്നു.

ഒരു ഇന്റർവ്യൂവിനു കാലിഫോർണിയയിൽ എത്തിയതാണു ഞാൻ. എയർപോർട്ടിൽ നിന്നു് എന്നെ കൂട്ടിക്കൊണ്ടു പോകാമെന്നു് സിബു പറഞ്ഞിരുന്നു. സിബുവും ഞാനും അതു വരെ തമ്മിൽ കണ്ടിട്ടില്ല. ബ്ലോഗിലൂടെയുള്ള പരിചയമേ ഉള്ളൂ.

ഇന്റർവ്യൂവിനു കുത്തിയിരുന്നു പഠിച്ച കൂട്ടത്തിൽ ഏറ്റവും അവസാനം പഠിച്ചതു ഗണിതമായിരുന്നു. ഇവർ പസിലുകളൊക്കെ ചോദിക്കുമെന്നാണു കേട്ടിട്ടുള്ളതു്. വിമാനത്തിലിരുന്നു വായിച്ചതു് പ്രോബബിളിറ്റി തിയറിയാണു്. അതിനാൽ വെളിയിൽ ഇറങ്ങിയപ്പോൾ കാണുന്നിടത്തെല്ലാം പ്രോബബിളിറ്റി കാണാൻ തുടങ്ങി. തല നേരേ നിൽക്കുന്നില്ല.

എയർപോർട്ടിന്റെ വെളിയിൽ ഇറങ്ങി. സിബുവിന്റെ പൊടി പോലുമില്ല. ഇനി ഇങ്ങേർ പറ്റിക്കുമോ? ഏയ് ഇല്ല, ഒരു ബ്ലോഗർ മറ്റൊരു ബ്ലോഗറെ പറ്റിക്കാനുള്ള സാദ്ധ്യത വളരെ കുറവാണു്. കൂടി വന്നാൽ കേസു കൊടുക്കും, അത്രയേ ഉള്ളൂ.

സിബുവിനെ വിളിച്ചു. സിബു വീട്ടിൽ നിന്നു് ഇറങ്ങുന്നതേ ഉള്ളൂ. “ഉമേഷേ, ഞാൻ പത്തു മിനിട്ടിൽ എത്തും. എന്റെ കൂടെ വരണം എന്നു പറഞ്ഞു് രണ്ടു ക്ടാങ്ങളും കൂടി ഭയങ്കര വഴക്കു്. അതാ ഇറങ്ങാൻ വൈകിയതു്. ഒരു വെള്ള നിസ്സാൻ സെൻ‌ട്രയാണു കാർ.” നമ്പർ പ്ലേറ്റിന്റെ അവസാനത്തെ മൂന്നു് അക്കങ്ങളും പറഞ്ഞുതന്നു.

ഒരു കാറിന്റെ നമ്പരിന്റെ അവസാനത്തെ മൂന്നു നമ്പരും അതു തന്നെയാവാൻ സാദ്ധ്യത 10 x 10 x 10 = ആയിരത്തിൽ ഒന്നു മാത്രമാണു്. അതൊരു വെള്ളക്കാറും കൂടി ആവാനോ? ഞാൻ ആലോചിച്ചു. മൊത്തം കാറുകളിൽ അഞ്ചിലൊന്നു വെളുപ്പാണെന്നു കേട്ടിട്ടുണ്ടു്. അപ്പോൾ നമ്പരും നിറവും അതു തന്നെയാവാൻ സാദ്ധ്യത അയ്യായിരത്തിൽ ഒന്നു്. അതൊരു നിസ്സാൻ സെൻ‌ട്രയും ആവാനോ? ആകെ കാറുകളിൽ എത്ര ശതമാനമാണു നിസ്സാൻ സെൻ‌ട്ര? ആ, ആർക്കറിയാം! ഒരു ഇരുനൂറിൽ ഒന്നെന്നു ചുമ്മാ കൂട്ടിയാൽ തന്നെ ഞാൻ കാറു തെറ്റി കയറാനുള്ള സാദ്ധ്യത ഒരു മില്യനിൽ ഒന്നാകും. ഇനി അതിലുള്ള ആൾ ഒരു സീരിയൽ കില്ലർ ആകാനും എന്നെ കൊന്നു വഴിയരികിൽ തള്ളാനും സാദ്ധ്യത പിന്നെയും കുറയും. ആ നമ്പരിൽ അവസാനിക്കുന്ന വെളുത്ത നിസ്സാൻ സെൻ‌ട്ര കണ്ടാൽ അതു സിബു തന്നെ ആയിരിക്കും. കയറുക തന്നെ.

കാറിന്റെ പ്രോബബിലിറ്റി ഒരു വഴിക്കാക്കിയപ്പോൾ സിബുവിന്റെ വീടിനെപ്പറ്റി ചിന്തിച്ചു. രണ്ടു കുട്ടികൾ ഉണ്ടെന്നു പറഞ്ഞു. ആണായിരിക്കുമോ പെണ്ണായിരിക്കുമോ? ആദ്യത്തേതു് ആണാവാനും പെണ്ണാവാനും സാദ്ധ്യത 1/2 വീതം. രണ്ടാമത്തേതിനും അതു തന്നെ. അങ്ങനെ നാലു രീതികൾ.

1. ആദ്യത്തേതു് ആണു്. രണ്ടാമത്തേതും ആണു്. സാദ്ധ്യത: 1/4.
2. ആദ്യത്തേതു് ആണു്. രണ്ടാമത്തേതു പെണ്ണു്. സാദ്ധ്യത: 1/4.
3. ആദ്യത്തേതു് പെണ്ണു്. രണ്ടാമത്തേതു് ആണു്. സാദ്ധ്യത: 1/4.
4. ആദ്യത്തേതു് പെണ്ണു്. രണ്ടാമത്തേതും പെണ്ണു്. സാദ്ധ്യത: 1/4.

അതായതു്, രണ്ടും ആണാവാൻ സാദ്ധ്യത 25%. രണ്ടും പെണ്ണാവാൻ സാദ്ധ്യത 25%. ഒന്നു് ആണും മറ്റേതു പെണ്ണും ആവാൻ സാദ്ധ്യത 50%.

ഇത്രയും ആലോചിച്ച്പ്പോഴേയ്ക്കും ഒരു വെളുത്ത നിസ്സാൻ സെൻ‌ട്ര ഓടിക്കിതച്ചു വന്നു് എന്നെയും കടന്നു പോയി മുന്നിൽ പോയി നിന്നു. അവിടെയുള്ള ഒരു പോലീസുകാരനോടു് അലാസ്ക എയർലൈൻസിൽ വരുന്നവർ എവിടെയാണു് ഇറങ്ങിനിൽക്കുക എന്നു് ഒരുത്തൻ ത്രിശ്ശൂർ ആക്സന്റുള്ള ഇംഗ്ലീഷിൽ ചോദിക്കുന്നതു കേട്ടു. “സംശയമില്ല, ഇതു സിബു തന്നെ” എന്നുറപ്പിച്ചു് ഞാൻ ഓടിച്ചെന്നു. എന്നെക്കൊണ്ടു് ഒരു ശ്ലോകം ചൊല്ലിച്ചു് ഞാൻ ആണെന്നു് ഉറപ്പുവരുത്തിയതിനു ശേഷം സിബു എന്നെ കാറിൽ കയറാൻ സമ്മതിച്ചു.

കാർ വിട്ടപ്പോൾ പുറകിൽ നിന്നു് ഒരു കിളിനാദം, “ഹലോ…”. പുറകിലെ സീറ്റിൽ ഒരു അഞ്ചുവയസ്സുകാരി സുന്ദരിക്കുട്ടി ഇരിക്കുന്നു.

സാദ്ധ്യതകളാകെ തകിടം മറിഞ്ഞു. അപ്പോൾ സിബുവിന്റെ രണ്ടു കുട്ടികളും ആണാവാനുള്ള സാദ്ധ്യത പൂജ്യം.

ഒന്നുകൂടി നോക്കിയപ്പോൾ ഇത്രയേ സാദ്ധ്യതയുള്ളൂ.

1. ആദ്യത്തേതു് ആണു്. രണ്ടാമത്തേതും ആണു്. സാദ്ധ്യത: 0.
2. ആദ്യത്തേതു് ആണു്. രണ്ടാമത്തേതു പെണ്ണു്. സാദ്ധ്യത: 1/3.
3. ആദ്യത്തേതു് പെണ്ണു്. രണ്ടാമത്തേതു് ആണു്. സാദ്ധ്യത: 1/3.
4. ആദ്യത്തേതു് പെണ്ണു്. രണ്ടാമത്തേതും പെണ്ണു്. സാദ്ധ്യത: 1/3.

അതായതു്, രണ്ടും ആണാവാൻ സാദ്ധ്യത 0. രണ്ടും പെണ്ണാവാൻ സാദ്ധ്യത 33.3333…%. ഒന്നു് ആണും മറ്റേതു പെണ്ണും ആവാൻ സാദ്ധ്യത 66.6666…%

“ഇളയ ക്ടാവു ഭയങ്കര വഴക്കായി പിണങ്ങിപ്പോയി. അതുകൊണ്ടു് ഇവളെ കൊണ്ടുപോന്നു,…” സിബു പറഞ്ഞു. അപ്പോൾ മൂത്തതു പെണ്ണാണു്. പ്രോബബിലിറ്റി പിന്നെയും തകിടം മറിഞ്ഞു.

1. ആദ്യത്തേതു് ആണു്. രണ്ടാമത്തേതും ആണു്. സാദ്ധ്യത: 0.
2. ആദ്യത്തേതു് ആണു്. രണ്ടാമത്തേതു പെണ്ണു്. സാദ്ധ്യത: 0.
3. ആദ്യത്തേതു് പെണ്ണു്. രണ്ടാമത്തേതു് ആണു്. സാദ്ധ്യത: 1/2.
4. ആദ്യത്തേതു് പെണ്ണു്. രണ്ടാമത്തേതും പെണ്ണു്. സാദ്ധ്യത: 1/2.

അതായതു്, രണ്ടും ആണാവാൻ സാദ്ധ്യത 0. രണ്ടും പെണ്ണാവാൻ സാദ്ധ്യത 50%. ഒന്നു് ആണും മറ്റേതു പെണ്ണും ആവാൻ സാദ്ധ്യത 50%.

സിബുവിന്റെ വീട്ടിൽ എത്തി. രണ്ടാമത്തെ മകൾ വാതിൽക്കൽ തന്നെ നിൽ‌പ്പുണ്ടായിരുന്നു. പിണക്കമൊക്കെ മാറി ചിരിച്ചുകൊണ്ടു്.

ഏറ്റവും പുതിയ പ്രൊബബിലിറ്റി.

1. ആദ്യത്തേതു് ആണു്. രണ്ടാമത്തേതും ആണു്. സാദ്ധ്യത: 0.
2. ആദ്യത്തേതു് ആണു്. രണ്ടാമത്തേതു പെണ്ണു്. സാദ്ധ്യത: 0.
3. ആദ്യത്തേതു് പെണ്ണു്. രണ്ടാമത്തേതു് ആണു്. സാദ്ധ്യത: 0.
4. ആദ്യത്തേതു് പെണ്ണു്. രണ്ടാമത്തേതും പെണ്ണു്. സാദ്ധ്യത: 1.

അതായതു്, രണ്ടും ആണാവാൻ സാദ്ധ്യത 0%. രണ്ടും പെണ്ണാവാൻ സാദ്ധ്യത 100%. ഒന്നു് ആണും മറ്റേതു പെണ്ണും ആവാൻ സാദ്ധ്യത 0%.

ഒരേ സംഭവത്തിനുള്ള സാദ്ധ്യത ഡാറ്റാ മാറുന്നതനുസരിച്ചു മാറുന്നതു നോക്കണേ!

വെള്ളെഴുത്തിന്റെ കർമ്മണിപ്രയോഗം എന്ന പോസ്റ്റിനെപ്പറ്റി ചില അഭിപ്രായങ്ങൾ:

• വെള്ളെഴുത്തു് എഴുതുന്നു:
  

  കള്ളം മാത്രം പറയുന്ന ഗ്രാമത്തില്‍ നിന്ന് ഒരാള്‍, സത്യം മാത്രം പറയുന്ന ഗ്രാമത്തില്‍ നിന്ന് ഒരാള്‍. ഇവര്‍ക്കു നടുവില്‍ നിന്നുകൊണ്ട്, കള്ളം പറയുന്നതാര് സത്യം പറയുന്നതാര് എന്നൊരു പിടിയുമില്ലാത്ത കാസ്പര്‍, കള്ളം പറയുന്നവരുടെ ഗ്രാമം ഏതാണെന്ന് കണ്ടുപിടിക്കണം. ഒരേയൊരു ചോദ്യമേ പാടുള്ളൂ. മുന്നില്‍ കാണുന്ന ഒരാളോട്, കള്ളന്മാരുടെ ഗ്രാമം ഏതാണെന്നു ചോദിച്ചാല്‍ അയാള്‍ പറഞ്ഞേക്കാവുന്ന ഉത്തരത്തിന്റെ വിരുദ്ധമായ ഗ്രാമമായിരിക്കും കള്ളന്മാരുടെ ഗ്രാമം. ഈ വിഷമപ്രശ്നത്തിന് അങ്ങനെയൊരു ഉത്തരം മാത്രമേ ഉള്ളൂ എന്നാണ് പ്രഫസറുടെ നിലപാട്. പ്രഫസര്‍ പറയുന്നത്, തുടര്‍ച്ചയായ രണ്ടു നിഷേധങ്ങള്‍ (നെഗറ്റീവുകള്‍)‍, ഒരാളിന്റെ ശരിയായ വ്യക്തിത്വത്തെ വെളിപ്പെടുത്താന്‍ സഹായിക്കുമെന്നാണ്.

  ഇതു തെറ്റാണു്. സത്യം പറയുന്ന ആളോടാണു് ഇതു ചോദിക്കുന്നതെങ്കിൽ ശരിയായ ഉത്തരം തന്നെയായിരിക്കും കിട്ടുന്നതു്.

  ഇതിനു് പല ഉത്തരങ്ങളുമുണ്ടു്. ഒരെണ്ണം ഇതാ: ഒരു ഗ്രാമത്തിലേയ്ക്കുള്ള വഴി ചൂണ്ടിക്കാണിച്ചുകൊണ്ടു് ഒരാളോടു ചോദിക്കുക: “ഇതു സത്യം പറയുന്നവരുടെ ഗ്രാമത്തിലേക്കുള്ള വഴിയാണോ എന്നു് മറ്റേ ആളോടു ചോദിച്ചാൽ അയാൾ എന്തു പറയും?” കിട്ടുന്ന ഉത്തരത്തിനു നേരേ എതിരായിരിക്കും സത്യം. True and False എന്നതും False and True എന്നതും False തന്നെയായിരിക്കും എന്ന boolean algebra-യിലെ തത്ത്വമാണു് ഇവിടെ ഉപയോഗിക്കുന്നതു്.

  നേരേ മറിച്ചു്, രണ്ടു നെഗേഷൻ True ആകുന്നതിനു് ഉദാഹരണം വേണമെങ്കിൽ “ഇതു സത്യഗ്രാമത്തിലേക്കുള്ള വഴിയാണോ എന്നു ചോദിച്ചാൽ സാധാരണ നീ എന്താണു പറയാറുള്ളതു്?” എന്നോ മറ്റോ ചോദിക്കണം. രണ്ടു ഗ്രാമത്തിൽ നിന്നുള്ള ഒരു പറ്റം ആളുകളെയോ ഏതു ഗ്രാമത്തിൽ നിന്നു് എന്നറിയാത്ത ഒരാളെ മാത്രമോ കണ്ടാൽ ഈ ചോദ്യം ചോദിക്കാം.

• വെള്ളെഴുത്തു് എഴുതുന്നു:
  

  ഈ കഥയ്ക്കുള്ള മറ്റൊരു വെര്‍ഷനില്‍ കള്ളം പറയുന്നവനെയും സത്യം മാത്രം പറയുന്നവനെയും കൂടാതെ കള്ളവും സത്യവും മാറിമാറി പറയുന്ന മറ്റൊരാളുകൂടി കടന്നു വരുന്നതു കാണാം. ജീവിതം എന്ന പ്രഹേളികയുടെ ഉത്തരം തന്നെ നേരെ കണ്ടെത്താന്‍ വയ്യാതെ അട്ടം നോക്കുന്നവന്റെ കുഴങ്ങുന്നവന്റെ ബാദ്ധ്യത വര്‍ദ്ധിപ്പിക്കാനായിട്ട് !

  വെള്ളെഴുത്തിനെ എന്റെ ഹ്രീഹ്ലാദവും ജഞ്ജലിപ്പും എന്ന പോസ്റ്റു വായിക്കാൻ ക്ഷണിക്കുന്നു. Boolean algebra-യിലെ xor എന്ന ക്രിയ കൊണ്ടു് അറിയേണ്ടാ‍ത്തതായ ഒരു ചരത്തെ ഒഴിവാക്കുന്ന ടെക്നിക്ക് ആണു് അതിൽ.

• വെള്ളെഴുത്തു് എഴുതുന്നു:
  

  പക്ഷേ കാസ്പറിനു പറയാന്‍ മറ്റൊരുത്തരമുണ്ടായിരുന്നു. വളരെ ലളിതമായത്. വരുന്നവനോട് ‘നീ മരത്തവളയാണോ’ എന്നു ചോദിക്കുക. അവന്‍ ‘അതെ’ എന്നു പറയുകയാണെങ്കില്‍ (കള്ളം മാത്രം പറയുന്നവന് മറ്റെന്തു പറ്റും?) അവന്‍ കള്ളന്മാരുടെ ഗ്രാമത്തില്‍ നിന്നാണെന്ന് ഉറപ്പിക്കാമല്ലോ.

  ഉറപ്പിക്കാം. പക്ഷേ അയാൾ ഏതു ഗ്രാമത്തിലേതാണു് എന്നതല്ല നമ്മുടെ പ്രശ്നം. ഏതാണു സത്യഗ്രാമത്തിലേയ്ക്കുള്ള വഴി എന്നതാണു്. ഈ മരത്തവളച്ചോദ്യം വേണ്ടാത്ത ചോദ്യത്തിന്റെ ഉത്തരത്തെയാണു തേടുന്നതു്.

• “ഒരു കൂട്ടത്തില്‍ 98 ശതമാനവും ചിന്തിക്കുന്നത് ഒരേ തരത്തിലായിരിക്കും…” എന്നു തുടങ്ങുന്ന ഖണ്ഡികയ്ക്കു് ഒരു സ്പെഷ്യൽ സല്യൂട്ട്!

മല്ലുവിനെ പള്ളു പറയൽ, യൂണിക്കോഡിനെ ആണിയടിക്കൽ, പോട്ടം പിടിക്കൽ, പോഡ് കാസ്റ്റു നടത്തൽ തുടങ്ങിയ കലാപരിപാടികൾക്കു ശേഷം നിഷാദ് കൈപ്പള്ളി അടുത്തിടയ്ക്കു കൈ വെച്ച മേഖലയാണു ഗോമ്പറ്റീഷൻ. അതു തുടങ്ങിയിട്ടു് ഇപ്പോൾ അതു കൈപ്പള്ളിക്കും നാട്ടുകാർക്കും അഡിൿഷൻ ആയെന്നാണു് റിപ്പോർട്ടു്. ഗോമ്പറ്റീഷൻ തുടങ്ങിയതിൽ പിന്നെ മറ്റു ബ്ലോഗ് പോസ്റ്റുകൾ വായിക്കാൻ ആളെക്കിട്ടുന്നില്ല എന്നാണു മിക്ക ബ്ലോഗന്മാരുടെയും ബ്ലോഗിനികളുടെയും പരാതി.

“ഇതാരുടെ പുസ്തകശേഖരം?” എന്ന സൂപ്പർഹിറ്റ് സീരീസിനു ശേഷം ഗോമ്പറ്റീഷനിലെ പുതിയ ഇനമാണു് “ഇതാരുടേ ഉത്തരങ്ങൾ”. (ആരുടേ എന്നു നീട്ടുന്നതു് മാള അരവിന്ദൻ ചോദിക്കുന്നതു പോലെയാണെന്നു കരുതിയാൽ മതി.) കുറേപ്പേരോടു കുറേ പൊട്ടച്ചോദ്യങ്ങൾ ചോദിക്കും. ആ ചോദ്യങ്ങളും അവർ കൊടുക്കുന്ന പൊട്ട ഉത്തരങ്ങളും കൂടി കൈപ്പള്ളി പ്രസിദ്ധീകരിക്കും. അതിൽ നിന്നു് വായനക്കാർ ഉത്തരം പറഞ്ഞ ആളെ കണ്ടുപിടിക്കണം. ഇതാണു മത്സരം. പലരോടു പല ചോദ്യങ്ങളാണു ചോദിക്കുക.

എന്നോടും ചോദിച്ചു മുപ്പതു ചോദ്യങ്ങൾ. തല്ലിക്കൊന്നാലും ബൂലോഗത്തിലെ ഏറ്റവും ബുദ്ധിശാലിക്കു പോലും മനസ്സിലാവരുതു് എന്ന വാശിയോടെ ഞാൻ വളഞ്ഞുകുത്തി തിരിഞ്ഞമർന്നു് ഓതിരം കടകം തുടങ്ങി പണി പതിനെട്ടും നോക്കി ഉത്തരം പറഞ്ഞു. അതിനനുഭവിച്ച വേദന ചെറുതല്ലായിരുന്നു. സംവൃതോകാരത്തെ ഉപേക്ഷിച്ചു. (പുഷ്പപാദുകം മാത്രം അകത്തേയ്ക്കു സ്വീകരിച്ചു് സംവൃതാ സുനിലിനെ പുറത്തു നിർത്തിയതിൽ സിജുവിനുണ്ടായ മാനസികവിഷമത്തിൽ മാപ്പു ചോദിക്കുന്നു.) അദ്ധ്യാപകനെ അധ്യാപകൻ എന്നെഴുതി. കഷ്ടപ്പെട്ടു മനസ്സിനെ നിയന്ത്രിച്ചു് ഒരു ശ്ലോകം പോലും ക്വോട്ടു ചെയ്തില്ല. ശ്ലോകം ചോദ്യമായി വന്നപ്പോൾ ഉത്തരമായി തോന്നിയവാസം പറഞ്ഞു. എന്നിട്ടും ഇടിവാളും തൊട്ടു പിന്നാലെ സിദ്ധാർത്ഥനും എന്നെ പൊക്കി. (“പ്രത്യക്ഷരലക്ഷം എന്നു് ഇനി എഴുതില്ല” എന്നു പ്രത്യക്ഷരലക്ഷം എഴുതണം!) നമിച്ചു മച്ചാ, നമിച്ചു!

ഇനി ആ ചോദ്യങ്ങളും എന്റെ ഉത്തരങ്ങളുടെ പൊരുളും.

1. എന്താണു് സമൂഹിക പ്രതിബദ്ധത?
   ഇതു് എന്നെ കുഴക്കിയിട്ടുള്ള ഒരു പ്രശ്നമാണു്. സമൂഹത്തിനു നല്ലതായതൊക്കെ സമൂഹത്തിനു കൊടുക്കുക എന്നൊക്കെ ഒഴുക്കൻ മട്ടിൽ പറയാമെങ്കിലും, കാര്യത്തിലേക്കു കടക്കുമ്പോൾ സംഗതി വളരെ അവ്യക്തമാകും.

   ഉദാഹരണമായി, പത്തുപതിനഞ്ചു കൊല്ലം മുമ്പു് ഗ്രഹനില, ജാതകം തുടങ്ങിയവ ഉണ്ടാക്കുന്ന ഒരു കമ്പ്യൂട്ടർ പ്രോഗ്രാം ലൈബ്രറി ഞാൻ ഉണ്ടാക്കിയിരുന്നു. അതു് ഇപ്പോഴും എന്റെ കയ്യിൽത്തന്നെ ഇരിക്കുന്നു. സ്വതന്ത്രമാക്കിയില്ല. ആക്കണോ വേണ്ടയോ എന്നു് തർക്കിക്കുമ്പോൾ ഈ സാമൂഹികപ്രതിബദ്ധത മനസ്സിൽ വരും.

   • വളരെയധികം ആളുകൾക്കു് ഉപയോഗമുള്ളതു്. കണ്ട കമ്പ്യൂട്ടർ ജാതകക്കാർക്കു് ആളുകൾ കൊടുക്കുന്ന കാശു നോക്കിയാൽ ഇതൊരു വലിയ ഉപകാരമാവും. സമൂഹത്തിനു് ഉപകാരമുണ്ടാവുന്ന കാര്യങ്ങൾ പ്രസിദ്ധീകരിക്കുക തന്നെ വേണം. മാത്രമല്ല, അതിനെ നന്നാക്കി വിവാഹപ്പൊരുത്തം, ഗൃഹപ്രവേശം, ചോറൂണു്, തിരണ്ടുകല്യാണം തുടങ്ങിയവയും ചേർക്കണം. അതാണു സാമൂഹികപ്രതിബദ്ധത – എന്നു് ഒരു വാദം.
   • ഭാരതത്തെ കാർന്നു തിന്നുന്ന ഏറ്റവും വലിയ ദുരിതങ്ങളിലൊന്നായ ജ്യോതിഷത്തെ ഒരു തരത്തിലും പ്രോത്സാഹിപ്പിക്കാതിരിക്കുക എന്നതാണു സാമൂഹികപ്രതിബദ്ധത. ഇതു പ്രസിദ്ധീകരിച്ചാൽ ഇതുപയോഗിച്ചു് ആളുകൾ കൂടുതൽ ജ്യോതിഷ-അന്ധവിശ്വാസ-ബിസിനസ്സുകൾ ഉണ്ടാക്കും. ഇത്രയും വലിയ ഒരു തെറ്റു സമൂഹത്തോടു ചെയ്യാനില്ല.

   ഇതു് ഒരു ഉദാഹരണം മാത്രം. സംസ്കൃതം, ശ്ലോകം, ഗണിതം, സമസ്യാപൂരണങ്ങൾ തുടങ്ങിയ പല വിഷയങ്ങളിലും ഈ സാമൂഹികപ്രതിബദ്ധതാപ്രഹേളിക പൊന്തി വരുന്നതു കാണാം. അതിനാൽ എന്റെ ഉത്തരം

   ആ…
2. എന്താണ്‌ സൌന്ദര്യം?

   സൌന്ദര്യത്തിനു് ശ്രീഹർഷൻ കൊടുത്ത നിർവ്വചനത്തെക്കാളും നല്ലതു് ഒരെണ്ണം ഞാൻ ഇതു വരെ കണ്ടിട്ടില്ല.

   ക്ഷണേ ക്ഷണേ യന്നവതാമുപൈതി
   തദേവ രൂപം രമണീയതായാഃ

   യത് (എന്താണോ) ക്ഷണേ ക്ഷണേ (ഓരോ നിമിഷത്തിലും) നവതാം ഉപൈതി (പുതുമ കൈക്കൊള്ളുന്നതു്), തത് ഏവ (അതു തന്നെയാണു്) രമണീയതായാഃ രൂപം (സൌന്ദര്യത്തിന്റെ രൂപം).

   അതു തന്നെയായിരുന്നു എന്റെ ഉത്തരവും:

   ഓരോ തവണ കാണുമ്പോഴും പുതിയതായി തോന്നുന്നത്.

   (ആരെങ്കിലും ഇതു വെച്ചു് എന്നെ മനസ്സിലാക്കുമെന്നു കരുതി. ഉണ്ടായില്ല.)

3. ഗായകന്‍, അദ്ധ്യാപകന്‍, കുശിനിക്കാരന്‍, ആശാരി, കോമാളി എന്നീ അഞ്ചു തൊഴിലുകളേ ലഭ്യമുള്ളു എന്നു വന്നാല്‍ താങ്കള്‍ ഏതു തിരഞ്ഞെടുക്കും?

   ചെയ്യാൻ പറ്റുന്ന രണ്ടു പണിയേ ഇതിലുള്ളൂ. അദ്ധ്യാപകനും കോമാളിയും. ഇതു രണ്ടും ഒരുപാടു കാലം ചെയ്തു പരിചയമുള്ളതുമാണു്. അതിനാൽ എന്റെ ഉത്തരം:

   അധ്യാപകൻ. ഞാൻ അല്ലെങ്കിലും കോമാളിയാണ്. മറ്റേ ജോലി പോയാലും രക്ഷപ്പെടും. സൈഡ് ബിസിനസ്സായി വേണമെങ്കിലും ചെയ്യാം.

   മറ്റു മൂന്നും രക്ഷയില്ല.

   വേണമെങ്കിൽ ആശാരിയുടെ കുശിനിക്കാരനെ പാട്ടു പഠിപ്പിക്കുന്ന കോമാളിയാവാം.

4. എന്താണ്‌ ദൈവം?

   സംസ്കൃതത്തിൽ “ദൈവം” എന്നു പറഞ്ഞാൽ “വിധി” എന്നാണു് അർത്ഥം. ക്രിസ്ത്യൻ പാതിരിമാരാണു് ഈശ്വരൻ എന്ന അർത്ഥത്തിൽ ആ വാക്കു് ഉപയോഗിച്ചു തുടങ്ങിയതു്. പിന്നെ അതു മലയാളത്തിൽ പ്രചാരത്തിലായി. “ദൈവമേ കൈതൊഴാം കേൾക്കുമാറാകണം” എന്നു പന്തളം കേരളവർമ്മ എഴുതുമ്പോഴേയ്ക്കും ഈ അർത്ഥം പ്രചാരത്തിലായിരുന്നു…

   …എന്നു വല്ലതും എഴുതിയാൽ ആ നിമിഷം എന്നെ പൊക്കും. പിന്നെ ദൈവത്തെപ്പറ്റി കുറേ ഫിലോസഫി ആലോചിച്ചു. ഒന്നും അങ്ങോട്ടു് ഇഷ്ടപ്പെട്ടില്ല. പിന്നെ ഇങ്ങനെ എഴുതി.

   ഒരു മിനിറ്റ്… ജബ്ബാർ മാഷിനോടു ചോദിച്ചിട്ടു പറയാം…
5. കായംകുളം കൊച്ചുണ്ണി, വെള്ളായണി പറമു, മുളമൂട്ടില്‍ അടിമ, ഇത്തിക്കര പക്കി, ജംബുലിംഗം തുടങ്ങിയവര്‍ ധനികരെ കവര്‍ന്ന് പാവങ്ങള്‍ക്കു നല്‍കുകയും നാട്ടുനീതി നടപ്പാക്കുകയും ചെയ്തിരുന്നു എന്ന വീരചരിതങ്ങള്‍ ഇഷ്ടമാണോ?
   ഫിക്‌ഷൻ എന്ന നിലയ്ക്കു വായിക്കാൻ ഇഷ്ടമാണ്. എന്നാൽ ഈ കഥകളെ ചരിത്രമാക്കുന്നതിനോടു യോജിപ്പില്ല. ഇവന്മാരൊക്കെ കള്ളന്മാരായിരുന്നു. ആടിനെ പട്ടിയും പട്ടിയെ ആടും ആക്കാൻ ആർക്കാണു കഴിയാത്തത്?

   ഇതു് എന്റെ ഉത്തരം തന്നെ.

6. കുയിലിനെയോ കൊറ്റിയേയോ കൂടുതലിഷ്ടം?
   കൊറ്റി. കറുത്തതിനെക്കാൾ വെളുത്തതിനെ ഇഷ്ടപ്പെടുന്നതാണല്ലോ നാട്ടുനടപ്പ്?

   ഇതിനെക്കാൾ നല്ല ഉത്തരം കിട്ടിയില്ല. “കൊറ്റി. കുയിലിന്റെ ടേസ്റ്റ് കാക്കയുടേതുപോലെ അല്ലേ?” എന്നതായിരുന്നു റണ്ണർ അപ്.

7. ഈയിടെയായി ഒറ്റയ്ക്കിരിക്കുമ്പോള്‍ ഒരു ഏകാന്തത അനുഭവപ്പെടാറുണ്ടെന്ന് തോന്നുന്നു?
   ഒരിക്കലുമില്ല. ഏകാന്തത അനുഭവപ്പെടുന്നത് സമാനമായ അഭിപ്രായമില്ലാത്തവരുടെ കൂടെ വർത്തമാനം പറയേണ്ടി വരുമ്പോഴാണ്.

   ഹൃദയത്തിൽ തട്ടിയുള്ള ഉത്തരം.

8. കഷ്ടകാലം എന്നാലെന്താണ്‌?
   ഇങ്ങനെയുള്ള പണ്ടാറമടങ്ങുന്ന ചോദ്യങ്ങൾക്ക് ഉത്തരം എഴുതേണ്ടി വരുന്നത്.

   ഹൃദയത്തിൽ തട്ടിയുള്ള വേറൊരു ഉത്തരം.

9. മോഹന്‍ലാല്‍ എന്തു തരം കഴിവുകള്‍ കൊണ്ടാണ്‌ സൂപ്പര്‍സ്റ്റാര്‍ ആയി അറിയപ്പെടുന്നത്‌?

   ഒരു മോഹൻ‌ലാൽ ഫാൻ ആയിരുന്ന ഞാൻ രണ്ടു പാരഗ്രാഫിൽ അദ്ദേഹത്തിന്റെ ഗുണഗണങ്ങൾ ഉദാഹരണസഹിതം വിവരിച്ചിട്ടു്, അതു മഹാബോറാണെന്നു തോന്നുകയാൽ മൊത്തം മായ്ച്ചു കളഞ്ഞിട്ടു് ഇങ്ങനെ എഴുതി:

   ആരു പറയുന്നു ലവൻ സൂപ്പറാണെന്ന്? ഫാൻസോ? ഫാൻസിനു ഷക്കീലാമ്മയും സൂപ്പറുകൾ തന്നേ?

   പെരിയോന്റെ പെരുമ എളിയോന്റെ പൃഷ്ഠത്തിലാണ് എന്നൊരു ചൊല്ലുണ്ട്. ഫാൻസ് ആണ് ഇവരെയൊക്കെ സൂപ്പർസ്റ്റാർ ആക്കുന്നത്.

   (പൃഷ്ഠത്തിന്റെ സ്പെല്ലിംഗ് ശരിയായതു കൊണ്ടു് എന്നെ കണ്ടുപിടിക്കുമെന്നു കരുതി. ഉണ്ടായില്ല.)

10. ബ്ലോഗിൽ അവസാനമായ എഴുതിയ post എന്തിനെഴുതി?
    ഒരു വാർത്ത വായിച്ചപ്പോൾ ചൊറിഞ്ഞുകയറി. പ്രതികരിക്കണമെന്നു തോന്നി. പ്രതികരിച്ചു. അത്രമാത്രം.

    വഴിതെറ്റിക്കുന്നതും എന്നാൽ സത്യസന്ധവുമായ ക്ലൂ. ഈ പോസ്റ്റായിരുന്നു എന്റെ അവസാനത്തെ പോസ്റ്റ്.

11. മോതിരം, മാല, വാച്ച്‌, ബ്രേസ്‌ലെറ്റ്‌ തുടങ്ങിയവ ധരിക്കാന്‍ ഇഷ്ടമാണോ?

    ആഭരണങ്ങൾ ഇഷ്ടമല്ല. പക്ഷേ അതെഴുതിയാൽ കള്ളമാകും. എന്റെ ഓർക്കുട്ട് പ്രൊഫൈലിൽ മാല വ്യക്തമായി കാണാം. അതുകൊണ്ടു്…

    ബ്രേസ്‌ലെറ്റ് ഇതു വരെ ധരിച്ചിട്ടില്ല. സമയം അറിയാനുള്ള ഏറ്റവും നല്ല വഴിയായി വാച്ച് കെട്ടാറുണ്ട്. കല്യാണത്തിനു ഭാര്യ (അയ്യോ, ഇതൊരു ക്ലൂ ആണല്ലോ, ബാച്ചി അല്ലെന്ന്! ആ, പോട്ടേ!) ഇട്ട മോതിരവും മാലയും ധരിക്കാറുണ്ട് കുടുംബകലഹം പേടിച്ച്.

    ഇതൊന്നും ധരിക്കാൻ അത്ര ഇഷ്ടം അല്ല.

    എന്നു മാത്രം എഴുതി വിട്ടു.

12. പുരുഷന്മാര്‍ മാര്‍സില്‍ നിന്നും സ്ത്രീകള്‍ വീനസില്‍ നിന്നുമുള്ളവരാണെന്ന് വിശ്വസിക്കുന്നോ?

    ഈ ചോദ്യത്തിന്റെ കൂടെ നൂറു വാക്കിൽ കുറയാതെ എന്നും ഉണ്ടായിരുന്നു. അതുകൊണ്ടാണു്

    ഇല്ല എന്നു നൂറു പ്രാവശ്യം എഴുതിയാൽ മതിയോ?

    എന്ന ഉത്തരം എഴുതിയതു്.

    പിന്നെ തോന്നി അതു പോരാ എന്നു്. മാഴ്സ് വീനസ് സീരീസിലെ മൂന്നു പുസ്തകം വായിച്ചിട്ടുള്ളതുകൊണ്ടു് (എന്റെ ശേഖരത്തിൽ ഒരെണ്ണം ഉണ്ടായിരുന്നു) അതിനെപ്പറ്റി നാലു ഡയലോഗ് പൂശണമെന്നു തോന്നി. അതുകൊണ്ടു്….

    സ്ത്രീപുരുഷന്മാരുടെ സ്വഭാവവൈചിത്ര്യം വിശദീകരിക്കാനുള്ള ഒരു തിയറി ആണത്. ആ തിയറി ദയനീയമായി പരാജയപ്പെടുകയും ചെയ്തു.

    അതിനു പകരം, “”Why men don’t listen and women cannot read maps”” എന്ന പുസ്തകം വായിക്കുക.

എന്നെഴുതി.

13. നിങ്ങൾ Ernest Hemingway-യെ ചന്തയിൽ മീൻ വാങ്ങൻ പോകുമ്പോൾ കണ്ടുമുട്ടിയാൽ എന്തു ചോദിക്കും?
    

    എന്തൊരു പൊട്ടച്ചോദ്യം! ഒരു കിഴവൻ കടലിൽ മീൻ പിടിക്കാൻ പോയ കഥ ഉള്ള കൊച്ചു പുസ്തകത്തിനു നോബൽ സമ്മാനം വാങ്ങിയ കക്ഷിയാണു് ഹെമിംഗ്‌വേ എന്നു പറഞ്ഞാൽ അങ്ങേരെപ്പറ്റിയുള്ള എന്റെ വിവരം തീർന്നു. ഇതല്ലാതെ ഒന്നും തോന്നിയില്ല.

    ഇതിൽ ഏതു മീനിനെ പിടിച്ചാൽ നോബൽ സമ്മാനം കിട്ടാൻ വകുപ്പുണ്ടാവും എന്ന്.
14. ഏറ്റവും വലുതെന്താണ്‌?

    കളിയിൽ അല്പം കാര്യം എന്ന സിനിമയിൽ മോഹൻലാൽ പറയുന്ന ആപ്തവാക്യം കട്ടെടുത്തു:

    എളിമ.
15. മലയാള ഭാഷയും, മാദ്ധ്യമവും എന്ന വിഷയത്തെ കുറിച്ചു് 200 വാക്കിൽ കുറയാതെ ഒരു ലേഖനം എഴുതുക.

    എഴുതിത്തുടങ്ങി. ഒരു പാരഗ്രാഫ് വായിച്ചപ്പോൾ അതിൽ എന്നെ മുഴുവനോടെ എഴുതിവെച്ചിരിക്കുന്നു. വെള്ളെഴുത്തു സ്റ്റൈലിൽ മാറ്റിയെഴുതിയാലോ എന്നു കരുതി. സമയം കിട്ടിയില്ല. അവസാനം സഹികെട്ടു് ഇങ്ങനെ എഴുതി:

    ഇരുനൂറു വാക്കിൽ കുറയാതെയോ? എനിക്കു വേറേ പണിയുണ്ട്…

    (ഇരുനൂറു വാക്ക് എഴുതാൻ സമയവും വകുപ്പും ഉണ്ടെങ്കിൽ ഞാനൊരു പോസ്റ്റിട്ടേനേ…)

16. പാമ്പിന്റെ രത്നം, കൊതിയന്റെ വിത്തം, സതീകുചം, കേസരി തന്റെ കേശം. തങ്കളുടെ അഭിപ്രായത്തില്‍ ഈ ഗണത്തില്‍ പെടുന്ന ഒരു മൂന്നെണ്ണം കൂടി പറയാമോ?

    ഉണ്ടെന്നു കേൾക്കുന്നതല്ലാതെ നേരിട്ടു കാണാനോ തൊടാനോ പറ്റാത്ത സാധനങ്ങളാണു് ഇവയെല്ലാം. (സതി = നല്ല സ്വഭാവമുള്ളവൾ, കേസരി = സിംഹം)

    എനിക്കു് ഈ ശ്ലോകം മുഴുവൻ അറിയില്ല. ദേവൻ ഇവിടെ പറഞ്ഞു കേട്ടിട്ടുണ്ടു്. കൈപ്പള്ളിയ്ക്കു് ഇതു പറഞ്ഞുകൊടുത്തതും ദേവനായിരിക്കും. സീയേക്കാരനാനെന്നു പറയുന്നു. സീയേയ്ക്കു പഠിക്കുന്നതല്ലാതെ ആ സാധനം പാസ്സായ ആരെയും ഇതു വരെ കണ്ടിട്ടില്ലാത്ത ഞാൻ അതു കൊണ്ടു്

    പാമ്പിന്റെ രത്നം, കൊതിയന്റെ വിത്തം,
    സതീകുചം, കേസരി തന്റെ കേശം
    സീയേയ്ക്കു പോയിട്ടു ജയിച്ച പത്രം
    ദേവോ ന ജാനാതി കുതോ മനുഷ്യഃ

    എന്നൊരു ശ്ലോകം കാച്ചിയാലോ എന്നു കരുതി. (“കുതോ മനുഷ്യഃ” എന്നു വെച്ചാൽ മനുഷ്യന്റെ കാര്യം പിന്നെ പറയേണ്ടല്ലോ എന്നു് അർത്ഥാപത്തിയതോ പിന്നെ വക്കാരി ചൊല്ലാനില്ലെന്ന യുക്തിയാം. അല്ലാത ദേവൻ കണ്ടിട്ടില്ലാത്ത ആറാമത്തെ സാധനമല്ല.) ശ്ലോകം കാച്ചിയാൽ ആളുകൾ ആ സെക്കന്റിൽ എന്നെ കാച്ചും എന്നറിയാവുന്നതു കൊണ്ടു കൺ‌ട്രോൾ ചെയ്തു. തോന്നിയവാസം എഴുതാം എന്നു കരുതി.

    സതിയുടെ കുചവും കേസരി ബാലകൃഷ്ണപിള്ളയുടെ കേശവും വെളുത്തതാണ്. കൊതിയന്റെ വിത്തം പൂത്തുപൂത്ത് വെളുത്തിട്ടുണ്ടാവും. പാമ്പിന്റെ രത്നം ഞാൻ കണ്ടിട്ടില്ല. അതും വെളുത്തതായിരിക്കും.

    അപ്പോൾ വെളുത്ത സാധനങ്ങൾ; പാൽ, മുട്ട, ഐരാവതം.

17. അല്ലാ, പൂച്ച ഏതു നിറമായാലും എലിയെപ്പിടിച്ചാല്‍ പോരേ?
    എലിയെ പിടിക്കുന്നതു മാത്രമാണു പൂച്ചയുടെ ധർമ്മം എന്നു കരുതുന്നതു തന്നെ തെറ്റ്. നിറം നോക്കി ഒരു മൃഗം പൂച്ചയാണോ പട്ടിയാണോ എന്നു തീരുമാനിക്കുന്ന പഴയ രീതിയെ പരിഷ്കരിച്ചതല്ലേ ഇത്?

    പൂച്ച എലിയെപ്പിടിച്ചു കൊണ്ടു വരുമ്പോൾ അതിന്റെ നിറം നോക്കാതിരുന്നാൽ മതി. എലിയുടെയും.

    സംഗതി സീരിയസ് ആയി. പണ്ടാറം!

18. നിങ്ങൾ Dinnerനു് ഈ പട്ടികയിൽ കൊടുത്തിരിക്കുന്ന രണ്ടു പേരിൽ ആരെ ക്ഷനിക്കും? അവർക്ക് എന്തു ഭക്ഷണം കൊടുക്കും? അവരോടു എന്തെല്ലാം ചോദിക്കും?
    1) ഗാന്ധി
    2) ഉമ്മർ ഫറൂഖ് (Kalifa)
    3) Jack the Ripper
    4) മമ്മൂട്ടി
    5) Nelson Madela
    6) Superman
    7) Stephen Spielberg
    8) Jimmy Wales
    9) Paulo Coelho
    10) Khalil Gibran
    11) Salman Rushdie
    12) കുറുമാൻ
    13) സാമ്പശിവൻ (കാഥികൻ)
    14) കൈപ്പള്ളി
    15) നാറാണത്തു ഭ്രാന്തൻ
    16) കുമാരനാശാൻ
    17) മാമുക്കോയ
    18) Charlie Chaplin
    19) വിശാല മനസ്കൻ (സജീവ് ഇടത്താടൻ)
    20) ഇഞ്ചിപ്പെണ്ണു്

    ഇങ്ങനെയുള്ള ചോദ്യം ചോദിക്കുന്നവരെയാണു് വേലിപ്പത്തലു വെച്ചു തല്ലേണ്ടതു്. കൈപ്പള്ളിയെ ഡിന്നറിനു വിളിച്ചിട്ടു കുറച്ചു മുളകുപൊടിയും വിമ്മും കലക്കിയ പുളിശ്ശേരി കുടിപ്പിക്കാം എന്നെഴുതണമെന്നു വിചാരിച്ചതാണു്. കൂട്ടിനാരെ വിളിക്കും എന്നു കിട്ടിയില്ല. അതിനാൽ വിശാലനെ വിളിക്കാം എന്നു കരുതി. ആര്യഭവനിൽ നിന്നു് ഒരു പഴം‌പൊരി വാങ്ങിക്കൊടുക്കാം എന്നു പറഞ്ഞാൽ അതും വലിയ ക്ലൂ ആകുമെന്നു പേടിച്ചു് പിന്നെയും കണ്ട്രോൾ ചെയ്തു.

    ഗാന്ധിയെയും വിശാലമനസ്കനെയും.

    ഗാന്ധി മിക്ക ദിവസവും ഉപവാസമാണ്. വിശാലന് കട്ടൻ കാപ്പിയും ആറു മുട്ട പുഴുങ്ങിയതും കൊടുത്താൽ മതി.

    ഡിന്നർ കൊടുക്കാൻ കോപ്പുണ്ടായിരുന്നെങ്കിൽ ഞാൻ മൂന്നാം ചോദ്യത്തിൽ കുശിനിക്കാരന്റെ പണി എടുത്തേനേ…

19. കൊട്ടാരക്കര ശ്രീധരൻ നായരെ ഉച്ചക്ക് 12 മണിക്കു റോടരുകിൽ കണ്ടാൽ എന്തു ചോദിക്കും?
    കൊട്ടാരക്കര എന്ന സ്ഥലപ്പേരും നായർ എന്ന വാലും സിനിമാനടന്റെ അച്ഛൻ ആണെന്നുള്ള പേരും കഴിഞ്ഞ തിരുവനന്തപുരം സമ്മേളനത്തിനു ശേഷവും ചുമന്നു കൊണ്ടു നടക്കാൻ നാണമില്ലേ എന്നു ചോദിക്കും.

    ഇതിലും നല്ല ഉത്തരം ഇതിനു കൊടുക്കാൻ എനിക്കറിയില്ല.

20. മാര്‍ജ്ജാരപ്രണയമോ ഹംസലീലയോ കൂടുതല്‍ മനോഹരം?
    രണ്ടും കണ്ടിട്ടില്ല. ശുനകഭോഗത്തെപ്പറ്റി വേണമെങ്കിൽ പറയാം.

    അറിയുന്നതല്ലേ പറയാൻ പറ്റൂ?

21. മലയാളം പത്രത്തില്‍ റവന്യൂ സൂപ്രണ്ട്‌ എന്ന ഇംഗ്ലീഷ്‌ പദവിക്കു പകരം ജമാബന്ദിശിരസ്തദാര്‍ എന്നെഴുതേണ്ടതുണ്ടോ? എക്സൈസ്‌ എന്നെഴുതുന്നതോ പിറവക എന്നെഴുതുന്നതോ കൂടുതല്‍ അഭികാമ്യം?
    അങ്ങനെ എഴുതുന്നവരെ മുക്കാലിയിൽ കെട്ടി പ്രത്യക്ഷരലക്ഷം തല്ലണം.

    ഐതിഹ്യമാലയിൽ കൊട്ടാരത്തിൽ ശങ്കുണ്ണി ചവറു പോലെ പ്രയോഗിച്ച പ്രത്യക്ഷരലക്ഷം ക്വോട്ടു ചെയ്തതു കൊണ്ടു മാത്രം എന്നെ സിദ്ധാർത്ഥൻ പൊക്കുമെന്നു കരുതിയില്ല. ഇതെന്താ വേറേ ആരും ഐതിഹ്യമാല വായിച്ചിട്ടില്ലേ?

    (“പ്രത്യക്ഷരലക്ഷം” എന്നു വെച്ചാൽ ഓരോ അക്ഷരത്തിനും ലക്ഷം എന്നർത്ഥം.)

22. കുട്ടിയായിരുന്നപ്പോള്‍ ആയിത്തീരണമെന്ന് ആഗ്രഹിച്ചതിനുമപ്പുറത്ത്‌ താങ്കളുയര്‍ന്നോ? എങ്കില്‍ അതില്‍ സന്തോഷിക്കുന്നുണ്ടോ?
    ഒരിക്കലും ഭാവിയെപ്പറ്റി ചിന്തിച്ചിരുന്നില്ല. ആരോ പറഞ്ഞ് ഐ. ഏ. എസ്. കാരനാകണമെന്നു പറഞ്ഞു കുറേക്കാലം നടന്നു. പിന്നെ അതു വിട്ടു. അതാകാഞ്ഞതിൽ സങ്കടമില്ല.

    മുതിർന്ന ശേഷം ആകണമെന്ന് ആഗ്രഹിച്ച കാര്യങ്ങളിൽ (ലിസ്റ്റു തന്നാൽ ക്ലൂ ആവും) ജേർണലിസ്റ്റ് ഒഴികെ എല്ലാം അല്പസമയത്തേക്കെങ്കിലും ആയി. സന്തോഷമേ ഉള്ളൂ.

    മുതിർന്നു കഴിഞ്ഞു് ആകാൻ ആഗ്രഹിച്ച കാര്യങ്ങൾ:

    1. സോഫ്റ്റ്‌വെയർ എഞ്ചിനീയർ: സിവിൽ എഞ്ചിനീയറിംഗ് പഠിച്ച കാലത്തു് കമ്പ്യൂട്ടറിലായിരുന്നു താത്പര്യം. സോഫ്റ്റ്വെയർ എഞ്ചിനീയർ ആകണമെന്നു് വലിയ ആഗ്രഹമായിരുന്നു. ആയി. കഴിഞ്ഞ പതിനെട്ടു കൊല്ലമായി അതു തന്നെ പണി.
    2. അദ്ധ്യാപകൻ: ഏറ്റവും ഇഷ്ടമുള്ള പണി. തിരുവനന്തപുരത്തു് ശ്രീകാര്യത്തു് ഒരു ട്യൂഷൻ സെന്ററിൽ കണക്കും ഫിസിക്സും പഠിപ്പിച്ചു. എൻ‌ട്രൻസ് കോച്ചിംഗും. ജോലി ചെയ്ത ഒരു കമ്പനിയിലെ ട്രെയിനിംഗ് ഡിപ്പാർട്ട്മെന്റിൽ ഏഴു മാസം ജോലി ചെയ്തു. കോബോൾ മുതൽ സീപ്ലസ്പ്ലസ് വരെയും ടെസ്റ്റിംഗ് തൊട്ടു് ഒബ്ജക്ട് ഓരിയന്റഡ് ഡിസൈൻ വരെയും പഠിപ്പിച്ചു. ഓറിഗണിലും കാലിഫോർണിയയിലും പിള്ളേരെ മലയാളം പഠിപ്പിക്കുന്ന സംരംഭങ്ങളിൽ പങ്കെടുത്തു. ഇപ്പോഴും തരം കിട്ടുമ്പോൾ പഠിപ്പിക്കുന്നു.
    3. ചെസ്സുകളിക്കാരൻ: നാട്ടിൽ വെച്ചു കളിച്ചിട്ടുണ്ടെങ്കിലും എസ്റ്റാബ്ലിഷ്ഡ് റേറ്റിംഗ് കിട്ടിയതു് അമേരിക്കയിൽ വന്നിട്ടാണു്. കറസ്പോണ്ടൻസ് ചെസ്സും കുറേ കളിച്ചു. അതിൽ രണ്ടു തവണ ഇന്ത്യയെ പ്രതിനിധീകരിച്ചു. പിന്നെ സമയക്കുറവു മൂലം നിർത്തി. എങ്കിലും വളരെ കളിച്ചു.
    4. എഴുത്തുകാരൻ: അവസാനം ബ്ലോഗിലൂടെ അതും സാധിച്ചു!

    അധികം ആഗ്രഹങ്ങളൊന്നും ബാക്കിയില്ല. ഹാപ്പി!

23. എന്താണ്‌ ശരിയല്ലാത്തത്‌?
    തെറ്റ്

    സിമ്പിൾ ചോദ്യം. സിമ്പിൾ ഉത്തരം!

24. എന്താണ്‌ സന്തോഷം?
    ഒരു കാര്യം മാത്രം മനസ്സിൽ നിറയുന്ന അവസ്ഥ.

    ഇതു് ഒറിജിനൽ ആണെന്നു തോന്നുന്നു. കൈപ്പള്ളിയുടെ ചോദ്യം കണ്ടതിനു ശേഷം തോന്നിയതു്. സന്തോഷിക്കുമ്പോൾ നമ്മുടെ മനസ്സിൽ സന്തോഷമുണ്ടാക്കിയ കാര്യം മാത്രമേ ഉണ്ടാവൂ. ദുഃഖിക്കുമ്പോൾ ഒരുപാടു കാര്യങ്ങൾ തിക്കിത്തിരക്കി വന്നു ബുദ്ധിമുട്ടിക്കും.

25. ആധുനിക കവിതകളെ കുറിച്ച് എന്താണു അഭിപ്രായം

    എന്റെ ഇനിയും എഴുതിത്തീരാത്ത “കവിതയും പദ്യവും” എന്ന പോസ്റ്റിൽ നിന്നു്:

    കവിത പഴയതായാലും പുതിയതായാലും ഒരു പോലെയാണ്. അത് ആസ്വദിക്കാൻ പറ്റുന്നവർക്ക് അത് ഇഷ്ടമാണ്. അല്ലാത്തവർക്ക് അത് അനാവശ്യവും.

    ആധുനികകവിത എന്നതു കൊണ്ട് ഉദ്ദേശിച്ചത് എന്താണ്? വൃത്തമില്ലാത്തതോ? അതു കവിതയുടെ വളർച്ചയിലെ ഒരു ഘട്ടം മാത്രം. ഏതു നാട്ടിലെ കവിത നോക്കിയാലും കാണാം, ആദ്യം പ്രാസം പോയി, പിന്നെ വൃത്തം പോയി, അതിനിടയിൽ കവിതയിൽ എന്തു പാടില്ല എന്നതിന്റെ അതിർവരമ്പുകൾ പോയി.

    ചവറുകൾ എല്ലാ സാഹിത്യത്തിലുമുണ്ട്. അടുത്ത കാലത്തെ കവിതകളിൽ അതല്പം കൂടുതലുണ്ട്. അതിനെ ആധുനികകവിതയായി ജെനറലൈസ് ചെയ്യേണ്ട കാര്യമില്ല.

26. ബ്ലോഗിൽ ഓർമ്മക്കുറിപ്പുകൾ എഴുതുന്നതിനെ കുറിച്ച് എന്താണു് അഭിപ്രായം
    വിശാലൻ എഴുതുന്നതുപോലെ രണ്ടാഴ്ചയിൽ ഒന്നു മാത്രം എഴുതുക. അല്ലെങ്കിൽ സ്റ്റോക്കു തീർന്നു പോകും.

    അല്ലെങ്കിൽ വക്കാരിയുടെ ഗതി വരും. ഡെയിലി മൂന്നു പോസ്റ്റിട്ട മനുഷ്യനാ. ഉറവ വറ്റി വറ്റി ഇപ്പോൾ തരിശായിപ്പോയില്ലേ…

27. മലയാളം ബ്ലോഗിൽ ഇഷ്ടപ്പെട്ട കവി ആരാണു്.
    പ്രമോദ്

    ലാപുടയാണു് ആദ്യം മനസ്സിൽ വന്നതു്. പക്ഷേ ഈയിടെയായി പ്രമോദിനെയാണു് കൂടുതൽ ഇഷ്ടം (ശ്ലോകവും എഴുതുന്നതു കൊണ്ടല്ല).

    (കൈപ്പള്ളിയും മോശമില്ല)

    “Poetry uses particular forms and conventions to suggest at alternative meanings in the words, or to evoke emotional or sensual responses.” എന്നു വിക്കിപീഡിയ. ഈ നിർവ്വചനമനുസരിച്ചു് കൈപ്പള്ളി എഴുതുന്നതും കവിതയല്ലേ? മനുഷ്യൻ മുമ്പു കണ്ടിട്ടില്ലാത്ത എന്തൊക്കെ രീതികളാണു് അങ്ങേർ മലയാളഭാഷയിൽ കൊണ്ടുവന്നതു്? ആരും സ്വപ്നത്തിൽ പോലും വിചാരിക്കാത്ത എന്തൊക്കെ അർത്ഥങ്ങളാണു് ഉണ്ടാക്കിയതു്? (പ്രവാസി, നാടു് തുടങ്ങിയവ ലേറ്റസ്റ്റ് ഉദാഹരണങ്ങൾ.) എല്ലാറ്റിലും അടങ്ങിയിരിക്കുന്ന ഇമോഷണലും സെൻഷ്വലും… ഹോ, അതൊന്നും പറയാതിരിക്കുകയാണു ഭേദം!

28. മലയാളം ബ്ലോഗിൽ ഇഷ്ടപ്പെട്ട ഓർമ്മ കുറുപ്പ്ist ആരാണു്
    അരവിന്ദൻ (മൊത്തം ചില്ലറ ഓർമ്മക്കുറിപ്പാണെങ്കിൽ)

    ഇടിവാൾ പറഞ്ഞതു പോലെ, ഞാൻ എന്നും അരവിന്ദന്റെ കട്ട ഫാൻ തന്നെ. അടുത്ത തവണ ഈ ക്ലൂ കൊടുക്കാതിരിക്കാൻ ശ്രമിക്കാം.

29. താങ്കളുടെ Camera ഏതാണു്?
    Point and Shoot

    ഒരു എസ്സെല്ലാർ വാങ്ങണമെന്നു് ഒരുപാടു കാലമായി വിചാരിക്കുന്നു. കാനൻ പവർ ഷോട്ടിലെ തന്നെ എല്ലാ സെറ്റിംഗ്സും ഇതു വരെ അറിയില്ല. പിന്നാ…

    (എന്നാലും ഇതു വായിച്ചിട്ടു് കൈപ്പള്ളി, സിബു എന്നൊക്കെ പറഞ്ഞവരെ സമ്മതിക്കണം!)

30. ഫോട്ടോ ബ്ലോഗുകളെ കുറിച്ചുള്ള അഭിപ്രായം
    ഫോട്ടോ ബ്ലോഗോ ഫോട്ടോഷോപ്പ് ബ്ലോഗോ?

ഡിജിറ്റൽ യുഗം ഫോട്ടോകളുടെ ചാരുത നഷ്ടപ്പെടുത്തി എന്നു കരുതുന്ന ഒരു പഴഞ്ചനാണു ഞാൻ.

റഷ്യയിൽ ഇപ്പോൾ (ഫെബ്രുവരി 17 മുതൽ 26 വരെ) ഒരു ചെസ്സ് ടൂർണമെന്റ് നടക്കുകയാണു്. എയറോഫ്ലോട്ട് ഓപ്പൻ ടൂർണമെന്റ്. 160 കളിക്കാർ പങ്കെടുക്കുന്ന ഒരു വലിയ ടൂർണമെന്റാണു് അതു്.

ഈ ടൂർണമെന്റിലെ ടോപ് സീഡ് കളിക്കാരൻ ശഖ്രിയാർ മമേദ്യരോവ് എന്ന അസർബൈജൻ ഗ്രാൻഡ്മാസ്റ്റർ ആണു്. 2008 ജനുവരിയിൽ റേറ്റിംഗ് കൊണ്ടു് ലോകത്തെ ആറാമത്തെ മികച്ച കളിക്കാരനായിരുന്ന മമേദ്യരോവ് ഇപ്പോൾ പതിനെട്ടാം സ്ഥാനത്താണു്.

ഈ ടൂർണമെന്റിലും ഇദ്ദേഹം നല്ല പ്രകടനമാണു കാഴ്ച വെച്ചതു്. ആദ്യത്തെ അഞ്ചു കളികളിൽ നാലു പോയിന്റോടെ വേറേ രണ്ടു ഗ്രാൻഡ്മാസ്റ്റർമാരോടൊപ്പം മുന്നിട്ടു നിൽക്കുകയായിരുന്നു കക്ഷി. അപ്പോഴാണു് അതു സംഭവിച്ചതു്.

ആറാമത്തെ കളിയിൽ തന്നെക്കാൾ നൂറു പോയിന്റ് താഴെയുള്ള ഇഗർ കുർണോസോവ് എന്ന റഷ്യൻ ഗ്രാൻഡ്മാസ്റ്ററോടു തോറ്റു.

ചില്വാനം തോൽ‌വിയൊന്നുമല്ല. വെറും ഇരുപത്തൊന്നു നീക്കത്തിൽ. ക്ലീൻ ബൌൾഡ്.

മമേദ്യരോവ് ഇതെങ്ങനെ സഹിക്കും? കുർണോസോവ് കളിയിൽ ചതി കാണിച്ചു എന്നു് ഒരു പരാതിയും കൊടുത്തു് അങ്ങേർ ടൂർണമെന്റിൽ നിന്നു പിന്മാറി. കളി തീർന്നതിനു ശേഷം Rybka എന്ന കമ്പ്യൂട്ടർ പ്രോഗ്രാം ഉപയോഗിച്ചു് അനലൈസ് ചെയ്തു നോക്കിയപ്പോൾ പ്രോഗ്രാം കളിച്ച നീക്കങ്ങളും കുർണോസോവ് കളിച്ച നീക്കങ്ങളും ഒന്നു തന്നെ എന്നു മനസ്സിലായത്രേ. കുർണോസോവിനു് ഈ പ്രോഗ്രാമിന്റെ സഹായം ലഭിച്ചിരുന്നു എന്നാണു് മമേദ്യരോവിന്റെ പരാതി.

കളിക്കിടെ ഓരോ നീക്കം കഴിഞ്ഞും (മറ്റേയാൾ ആലോചിക്കുമ്പോൾ) കുർണോസോവ് എഴുനേറ്റു ബാത്ത്‌റൂമിൽ പോയത്രേ. പോയപ്പൊഴൊക്കെ കസേരയിൽ ഇട്ടിരുന്ന കോട്ടുമെടുത്താണു പോയതത്രേ. കോട്ടിനുള്ളിൽ വല്ല കമ്പ്യൂട്ടറോ മറ്റോ…

പരാതി കിട്ടിയപ്പോൾ ടൂർണമെന്റ് ഭാരവാഹികൾ കുർണോസോവിന്റെ കോട്ടു് അഴിച്ചുവാങ്ങി പരിശോധിച്ചു. കിട്ടിയതു് ഒരു പായ്ക്കറ്റ് സിഗരറ്റും ഒരു ലൈറ്ററും ഒരു പേനയും മാത്രം. മാത്രമല്ല, ഓരോ നീക്കത്തിനും ശേഷം അങ്ങേർ എഴുനേറ്റു പോയതു് ടോയ്ലറ്റിലേക്കല്ല, പുറത്തു സിഗരറ്റു വലിക്കാനായിരുന്നു എന്നു ദൃക്‌സാക്ഷികൾ പറഞ്ഞു. സിഗരറ്റു വലിക്കാൻ വെളിയിൽ പോകണം. വെളിയിൽ തണുപ്പായതുകൊണ്ടാണു കോട്ടു് എടുത്തതു്.

ഇതൊക്കെ കേട്ടാൻ തോന്നും സാധാരണ മനുഷ്യന്മാർക്കു കളിക്കാൻ പറ്റാത്ത ഏതോ ഭീകരനീക്കങ്ങൾ കുർണോസോവ് നീക്കിയെന്നു്. ദാ ഇതാണു കളി:

ഇതിൽ 16. Rd4 വരെ ഇതിനു മുമ്പു കളിച്ചിട്ടുള്ളതാണു്. ഇത്രയും നീക്കങ്ങൾ കൊണ്ടു തന്നെ കറുപ്പിനു മുൻ‌തൂക്കം കിട്ടുകയും ചെയ്തു. ഇതിനു മുമ്പു് പതിനാറാം നീക്കത്തിൽ കുതിരയെ തിരിച്ചു വലിക്കുകയാണു് (16…Nd6) കറുപ്പു ചെയ്തിട്ടുള്ളതു്. അതിനു പകരം ഈ കളിയിൽ മന്ത്രി ഉപയോഗിച്ചു് (16…Qd6) വെളുത്ത ആനയെ (h6-ൽ ഇരിക്കുന്ന ആന) ആക്രമിച്ചു. “നീ എന്റെ കുതിരയെ എടുത്താൽ ഞാൻ നിന്റെ ആനയെ തട്ടും” എന്ന ലൈൻ. (ചെസ്സിൽ ആനയ്ക്കും കുതിരയ്ക്കും സാധാരണഗതിയിൽ ഒരേ വിലയാണു്.) ഇനി ആദ്യം മറ്റേയാൾ ആനകൊണ്ടു് ആനയെ എടുത്താലും തിരിച്ചു തേരു കൊണ്ടു് എടുക്കുമ്പോൾ വെളുപ്പിന്റെ മന്ത്രിയെ ആക്രമിക്കുന്നതുകൊണ്ടു് കറുപ്പിനു് തന്റെ കുതിരയെ രക്ഷിക്കാൻ സമയവും കിട്ടും. ഈ നീക്കം കുർണോസോവ് തന്നെ ഹോം അനാലിസിസിൽ (കമ്പ്യൂട്ടർ ഉപയോഗിച്ചോ അല്ലാതെയോ) കണ്ടുപിടിച്ചതാവാം. ഇങ്ങനെ ഗ്രാൻഡ്മാസ്റ്റർമാർ ഹോംവർക്ക് ചെയ്യാറുണ്ടു്. അതിനു കമ്പ്യൂട്ടർ ഉപയോഗിക്കുന്നതിൽ നിയമതടസ്സമില്ല താനും.

പിന്നീടുള്ള നീക്കങ്ങളൊക്കെ പ്രവചിക്കാൻ പറ്റുന്നവ തന്നെ. വെളുപ്പിനു വലിയ ഗത്യന്തരമൊന്നുമില്ല. പത്തൊൻപതാം നീക്കം വരെ ഇതാണു സ്ഥിതി. ഏതു സാധാരണ കളിക്കാരനും ഇത്രയും പുഷ്പം പോലെ കളിക്കും.

കളി കളഞ്ഞതു മമേദ്യരോവ് തന്നെയാണു്. 20. Nge2 കളിച്ചു് കഷ്ടിച്ചു രക്ഷപ്പെടാൻ നോക്കാതെ 20. fxe4 കളിച്ചു. അതിനു് കുർണോസോവ് കളിച്ച 20…Bg4 ഒരു സാധാരണ കളിക്കാരനു കളിക്കാവുന്നതേ ഉള്ളൂ.

ഈ കളിയിൽ ആകെ ഒരു അടിപൊളി നീക്കം എന്നു പറയാൻ (സാധാരണ കളിക്കാർ കാണാത്ത നീക്കം) കറുപ്പിന്റെ അവസാനത്തെ നീക്കമാണു്. 21…Qd2! മന്ത്രിയെ തേരിനു വെട്ടാൻ പാകത്തിൽ വെയ്ക്കുന്ന നീക്കം. വെളുത്ത മന്ത്രിയും അടി പതറി ഇരിക്കുകയായതിനാൽ എല്ലാം കലങ്ങിത്തെളിയുമ്പോൾ രണ്ടു മന്ത്രിമാരും വെട്ടിപ്പോവുകയും കറുപ്പിനു് ആനയ്ക്കു പകരം തേരു കിട്ടുകയും ചെയ്യും എന്നതാണു് ഈ നീക്കത്തിന്റെ ഗുണം. 21…Qd2-ന്റെ ഭീഷണി b2-വിലെ അടിയറവാണു്. 22. Rxd2 Nxd2+ 23. Kc1 Bxh5 24. Rxh5 Nf1 കളിച്ചാൽ കറുപ്പിനു് കുതിരയ്ക്കു പകരം തേരുണ്ടു്, ജയിക്കാൻ അതു മതി. അല്ലെങ്കിൽ 23. Na4 Bxh5 24. Rxd2 Nxd2+ 25. Kc1 Bxe2 26. Kxd2 Rxg2 എന്നതും കറുപ്പിനു ജയിക്കാൻ പര്യാപ്തമാണു്.

ഈ നീക്കം കാണാൻ ഒരു ഗ്രാൻഡ്മാസ്റ്റർക്കു കഴിയില്ലേ എന്നു ചോദിച്ചാൽ കഴിയും എന്നു തന്നെയാണു് ഉത്തരം. ഇതിനെക്കാൾ സങ്കീർണ്ണമായ നീക്കങ്ങൾ കേരളത്തിലെ സ്റ്റേറ്റ് ലെവൽ കളിക്കാർ കളിക്കാറുണ്ടു്.

അപ്പോൾ എന്താണു സംഭവിച്ചതു്?

കറുപ്പിന്റെ പതിനാറാമത്തെ നീക്കം അപ്രതീക്ഷിതമായ അടിയായ മമേദ്യരോവ് പിന്നീടുള്ള നീക്കങ്ങൾക്കു് വളരെ ആലോചിച്ചുകാണും. അതിലെ ഓരോ നീക്കത്തിലും സിഗരറ്റ് വലിക്കാനോ കാറ്റു കൊള്ളാനോ മറ്റേയാൾ എഴുനേറ്റു പോയിട്ടുണ്ടാവാം. ഇങ്ങനെ എഴുനേറ്റു പോകുന്നതു് ടൂർണമെന്റുകളിൽ സാധാരണമാണു്. താൻ കുത്തിപ്പിടിച്ചിരുന്നു് ആലോചിക്കുമ്പോൾ തന്നെക്കാൾ റേറ്റിംഗ് വളരെക്കുറവുള്ള എതിരാളി ഈസിയായി ഇടയ്ക്കുള്ള സമയത്തു് എഴുനേറ്റു പോയതു് അങ്ങേർക്കു സഹിച്ചു കാണില്ല. ഫലമോ, പിന്നെയും മോശമായി കളിച്ചു. തോൽക്കുകയും ചെയ്തു.

കളി തോറ്റാൽ ചതിയെന്നു പറയുന്നതു് എന്തായാലും വിചിത്രം തന്നെ. സ്ലം ഡോഗ് മില്യനറിലെപ്പോലെ പിടിച്ചു് ഇഞ്ചപ്പരുവം ചതച്ചു് പൂഴ്ത്തിവെച്ചിരിക്കുന്ന കമ്പ്യൂട്ടർ ചിപ്പ് കണ്ടുപിടിക്കാൻ ശ്രമിച്ചിരുന്നെങ്കിൽ ജോറായേനേ!

കമ്പ്യൂട്ടറിനെ വെല്ലുന്ന കോംബിനേഷനുകൾ ഗ്രാൻഡ്മാസ്റ്റർമാർ എന്നും കളിച്ചിരുന്നു. സ്റ്റെയിനിറ്റ്സിന്റെ പ്രസിദ്ധമായ 14 നീക്കം മുന്നിൽ കണ്ട കോംബിനേഷൻ, ബൈർണെതിരേ പതിമൂന്നുകാരൻ ബോബി ഫിഷർ മന്ത്രിയെ ബലി കഴിച്ചു ജയിച്ചതു്, ഫാൽക്ക്ബീർ കൌണ്ടർ അറ്റായ്ക്കിൽ സ്പീൽമാനെതിരേ തരാഷ് കളിച്ച ബിഷപ്പ് സാക്രിഫൈസ്, അഡോൽഫ് ആൻഡേഴ്സന്റെ രണ്ടു പ്രശസ്തകളികൾ – ഇതൊന്നും ഇപ്പോഴും കമ്പ്യൂട്ടറിനു് കണ്ടുപിടിക്കാൻ പറ്റാത്തവയാണു്. ബോർഡിൽ കണ്ടുപിടിക്കുന്നവ കൂടാതെ വീട്ടിലിരുന്നു തയ്യാറാവുന്ന ഓപ്പനിംഗ് കോംബിനേഷനുകളും ഉണ്ടു്. സ്പീൽമാനെതിരേ ബോട്ട്‌വിനിക് പണ്ടു കളിച്ച കാരോ-കാൻ പാനോവ് അറ്റായ്ക്ക് നീക്കവും ആനന്ദിനെതിരേ ലോകചാമ്പ്യൻഷിപ്പിൽ കാസ്പറോവ് കളിച്ച ഓപ്പൺ റുയ് ലോപ്പസ് നീക്കവും ഉദാഹരണങ്ങൾ.

എന്തായാലും ഇതൊരു വലിയ വിവാദമായിരിക്കുകയാണു്. അടിസ്ഥാനമില്ലാതെ ആരോപണമുന്നയിച്ച മമേദ്യരോവിനെതിരേ നടപടിയെടുക്കണം എന്നും ഒരു വിഭാഗം ആളുകൾ ആവശ്യപ്പെടുന്നു. കൂടുതൽ വിവരങ്ങൾ ഇവിടെയും ഇവിടെയും വായിക്കാം. സൂസൻ പോൾഗാറിന്റെ ഈ ബ്ലോഗ് പോസ്റ്റിലും.

അങ്ങനെ വേലായുധന്റെ ദിവസം കഴിഞ്ഞു. രാമസേനയിലെ വാനരന്മാർ എന്തു ചെയ്തു എന്നറിയില്ല. അവർക്കു കിട്ടിയ പിങ്കു നിറമുള്ള ഷഡ്ഡികൾക്കു് എന്തു പറ്റിയെന്നും അറിയില്ല.

കുഴൂർ വിത്സനും സന്തോഷും എഴുതിയ പ്രണയദിനകവിതകൾ വായിച്ചല്ലോ. ഇനി വാലന്റൈൻ ദിവസം കഴിഞ്ഞ സ്ഥിതിക്കു് നമുക്കു് പ്രണയം നഷ്ടമായവർക്കു വേണ്ടി ഒരു കവിത ചൊല്ലാം.

കാത്തിരിക്ക എന്ന മനോഹരകവിത എഴുതിയ റഷ്യൻ കവി കോൺസ്റ്റാന്റിൻ സിമോണോവിന്റെ മയക്കം (ЛЕТАРГИЯ) എന്ന കവിതയുടെ പരിഭാഷ വായിക്കൂ. (“ഓമനക്കുട്ടൻ ഗോവിന്ദൻ…” അല്ലെങ്കിൽ “ആരു വാങ്ങുമിന്നാരു വാങ്ങും…” എന്ന ഈണത്തിൽ വായിക്കുക.)

പതിനെട്ടു കൊല്ലത്തിനു ശേഷമാണു് ഒരു റഷ്യൻ കവിത പരിഭാഷപ്പെടുത്തുന്നതു്. പണ്ടു പഠിച്ച റഷ്യനൊക്കെ മറന്നു പോയിരിക്കുന്നു. വാലന്റൈൻസ് ഡേയ്ക്കു വേണ്ടി ഒന്നു രണ്ടു റഷ്യൻ പ്രണയകവിതകൾ പരിഭാഷപ്പെടുത്താൻ ശ്രമിച്ചിട്ടു് ഒന്നും ശരിയായില്ല. അപ്പോഴാണു് ഇതു ശ്രമിച്ചതു്.

ഇരുപതു കൊല്ലം മുമ്പു് ഇതൊന്നു പരിഭാഷപ്പെടുത്താൻ ശ്രമിച്ചിരുന്നു. അതു നഷ്ടപ്പെട്ടു പോയി. അവസാനത്തേതൊഴികെ എല്ലാ പദ്യങ്ങളും വസന്തതിലകത്തിലായിരുന്നെന്നും അവസാനത്തേതു മാലിനിയിലായിരുന്നു എന്നും ഓർമ്മയുണ്ടു്. ഓർമ്മയുള്ള തുടക്കവും ഒടുക്കവും:

മുത്തശ്ശി ചൊന്ന കഥയാ; ണൊരു പെൺ‌കിടാവു്,
നിദ്രാവിമുക്ത,….
…..
…..
ഇരുപതു ദിവസത്തേയ്ക്കെന്നെ മൂടായ്കയെന്നോ?

അതു നഷ്ടപ്പെട്ടു പോയതു് ഏതായാലും നന്നായി!

മനുഷ്യനിപ്പോൾ മാനം മര്യാദയ്ക്കു വ്യക്തിഹത്യ ചെയ്യാനും പറ്റില്ലത്രേ!

ആളുകളെ അധിക്ഷേപിക്കൽ, ഹേറ്റ് സ്പീച്ച്, ആക്ഷേപഹാസ്യം ആദിയായ കലാപരിപാടികൾ ബ്ലോഗിൽ ചെയ്താൽ ഐപ്പീസിയോ ഐട്ടിനിയമമോ 67 എന്നൊരു സാധനം ഉപയോഗിച്ചു കേസു കൊടുക്കുമത്രേ!

ഇതു പണ്ടേ കണ്ടതുകൊണ്ടല്ലേ ഞാൻ വ്യക്തിഹത്യയ്ക്കു് ഈ ബ്ലോഗ് ഉപയോഗിക്കാത്തതു്. അതിനു വേണ്ടി തുടങ്ങിയ ബ്ലോഗാണു് ബുദ്ധിപരീക്ഷ.

മേൽ‌പ്പറഞ്ഞ ഐപ്പീസി/ഐട്ടി നിയമത്തിലൊരു ലൂപ്പ്‌ഹോളുണ്ടു്. അതായതു്, “ഗണിതം, ധനതത്ത്വശാസ്ത്രം, വൈരുദ്ധ്യാത്മകഭൌതികവാദം, പക്ഷിശാസ്ത്രം, കോടാങ്കിശാസ്ത്രം, ജ്യോതിഷം തുടങ്ങിയ ശാസ്ത്രങ്ങളിലെ പ്രഹേളികകൾ അനാവരണം ചെയ്യുന്ന കൃതികളിലുള്ള വ്യക്തി-സമൂഹ-ഹത്യകൾ ഈ നിയമത്തിന്റെ പരിധിയിൽ വരികില്ല” എന്നു്.

അതുകൊണ്ടാണു് ഞാൻ ബുദ്ധിപരീക്ഷ എന്ന ബ്ലോഗ് തുടങ്ങിയതു്. പുറത്തു നിന്നു നോക്കിയാൽ പസ്സിൽ ബ്ലോഗാണു്. അകത്തു കടന്നാലോ, വിശാലമായ വ്യക്തിഹത്യയും.

വിശാലമനസ്കനെ വധിച്ചു കൊണ്ടായിരുന്നു തുടക്കം – എടത്താടൻ മുത്തപ്പനും ചെക്കിലെ പിശകും. പിന്നെ കലേഷ്, സിദ്ധാർത്ഥൻ, ദിൽബാസുരൻ, ദേവൻ, കുറുമാൻ, വിശാലൻ, തറവാടി, വല്യമ്മായി തുടങ്ങി യൂയേയിക്കാരെ വധിച്ചുകൊണ്ടുള്ള യു. എ. ഇ. മീറ്റും മണ്ണെണ്ണയും. വക്കാരിയെയും ചിത്രകാരനെയും ഒക്കെ വധിക്കാൻ പോയിട്ടു് അവസാനം ഷിജു അലക്സിനെ കൊന്നു കൊലവിളിച്ച ഹ്രീഹ്ലാദവും ജഞ്ജലിപ്പും ആയിരുന്നു ഈ സിരീസിലെ അവസാനത്തെ പോസ്റ്റ്.

നിങ്ങൾ ഇതുവരെ അതു വായിച്ചിട്ടില്ലെങ്കിൽ, നിങ്ങൾക്കു പസ്സിലുകളോ വ്യക്തിഹത്യയോ രണ്ടുമോ ഇഷ്ടമാണെങ്കിൽ, വായിക്കുക. ഇൻഡക്സ് ഇവിടെ ഉണ്ടു്.

അവിടെ കമന്റുകൾ മോഡറേറ്റഡ് ആണു്. അയച്ച ഉത്തരങ്ങൾ ആരും കാണാതിരിക്കാനാണതു്. ഉത്തരവും അയച്ചവരുടെ വിവരങ്ങളും പിന്നീടു പ്രസിദ്ധീകരിക്കും.

ഈ ബ്ലോഗിലെ ഏറ്റവും പുതിയ പോസ്റ്റാണു് ക്രിക്കറ്റ് മണ്ടത്തരങ്ങൾ. ഈ വരുന്ന മുപ്പത്തൊന്നാം തീയതി വിവാഹിതനാകുന്ന ശ്രീജിത്തിനു് എന്റെ സമ്മാനം. എഴുതാൻ തുടങ്ങിയിട്ടു് ഒരു കൊല്ലത്തിലധികമായെങ്കിലും ശ്രീജിത്ത് അമേരിക്കയിൽ നിന്നു് ഇന്ത്യയിലേക്കു പ്ലെയിനിൽ ഇരിക്കുന്ന സമയത്താണു് ഇതു പോസ്റ്റ് ചെയ്തതു്. ശ്രീജിത്ത് കൂടാതെ ആദിത്യൻ, നളൻ, തഥാഗതൻ, ചന്ത്രക്കാറൻ, കൊച്ചുത്രേസ്യ, മഴനൂലുകൾ, ജ്യോതിട്ടീച്ചർ എന്നിവരാണു് ഇതിലെ കഥാപാത്രങ്ങൾ. ഇനി ഇങ്ങനെ കൊല്ലപ്പെടാൻ സന്നദ്ധതയുള്ള ബാംഗ്ലൂർ ബ്ലോഗേഴ്സ് ബാക്കിയുണ്ടെങ്കിൽ ക്യൂവിൽ നിന്നു ടോക്കൻ എടുക്കേണ്ടതാണു്.

90% തീർന്നിരിക്കുന്ന പോസ്റ്റുകൾ തീർത്തു പബ്ലിഷ് ചെയ്യുക എന്ന പരിപാടിയുടെ ഭാഗമായി പ്രസിദ്ധീകരിച്ചതാണു് ഈ പോസ്റ്റ്.

ഒരു കൊല്ലം മുമ്പു്, കൃത്യമായി പറഞ്ഞാൽ 2008 ജനുവരി 16-നു് ഞാൻ കാർട്ടൂണിസ്റ്റ് സജ്ജീവിനോടു ഗൂഗിൾ ചാറ്റിൽ ചോദിച്ചു:

“ഗുരോ, ശ്രീജിത്ത് ക്രിക്കറ്റു കളിക്കുന്ന ഒരു പടം വരച്ചുതരാമോ? ഒരു പോസ്റ്റിൽ ഇടാനാണു്.”

കൃത്യം ഇരുപതു മിനിട്ടു കഴിഞ്ഞപ്പോൾ പടം റെഡി.

അതിനു ശേഷം ഒരു പത്തു തവണയെങ്കിലും ആ പോസ്റ്റു പബ്ലിഷ് ചെയ്തോ എന്നു് സജ്ജീവ് ചോദിച്ചിട്ടുണ്ടു്. എന്റെ മടി മൂലം ഇതുവരെ അതു നടന്നില്ല. കുറെക്കഴിഞ്ഞു്, എന്നാൽ എന്റെ പടം തിരിച്ചു തരൂ എന്നു വിലപിച്ചു. ഞാൻ കൊടുത്തില്ല.

കാർട്ടൂണിസ്റ്റ് സജ്ജീവിനു് ആയിരം നന്ദി.

ക്രിക്കറ്റ്, ബാംഗ്ലൂരിന്റെ ഭൂമിശാസ്ത്രം എന്നിവയെപ്പറ്റി ഒരു വിവരവുമില്ലാത്ത (ബൌളിംഗ് ആവറേജിനെ റൺ റേറ്റ് എന്നായിരുന്നു ഞാൻ എഴുതിയിരുന്നതു്!) എന്നെ ഈ പോസ്റ്റിലേയ്ക്കാവശ്യമായ വിവരങ്ങൾ തന്നു സഹായിക്കുകയും പോസ്റ്റ് തിരുത്തിത്തരുകയും ചെയ്ത ചില മഹാവ്യക്തികളുണ്ടു്. കേസ് വന്നാൽ അവർക്കും പ്രശ്നമാകും എന്നുള്ളതു കൊണ്ടു് ആരുടെയും പേരു പ്രസിദ്ധീകരിക്കുന്നില്ല. എല്ലാവർക്കും നന്ദി.

അക്കുത്തിക്കുത്തുകളി ഒരിക്കലെങ്കിലും കളിച്ചിട്ടില്ലാത്തവർ ചുരുക്കമായിരിക്കും. ഇതു കേരളത്തിൽ മാത്രം ഒതുങ്ങി നിൽക്കുന്ന കളിയല്ല. ലോകത്തിൽ മിക്ക സ്ഥലങ്ങളിലും ഇതിന്റെ വകഭേദങ്ങൾ റാൻഡമായി ഒരാളെ തിരഞ്ഞെടുക്കാൻ കുട്ടികൾ ഉപയോഗിക്കുന്നുണ്ടു്.

ഇസ്രയേലിൽ റഷ്യൻ ജൂതക്കുട്ടികൾ ഈ കളി കളിക്കുന്നതു കണ്ടിട്ടു് ഡാലി ഫോട്ടോ സഹിതം ഇട്ട കുട്ടികളികൾ (കുട്ടികളികൾ അല്ല ഡാലീ, കുട്ടിക്കളികൾ. ദ്വിത്വസന്ധി!) ആണു് മലയാളം ബ്ലോഗിൽ ഈ കളിയെപ്പറ്റി വന്ന ആദ്യത്തെ വിശദമായ പോസ്റ്റ്. അതിനു കിട്ടിയ കമന്റുകളിൽ നിന്നു പ്രചോദിതയായ ഡാലി പിന്നീടു് ‘അത്തള പിത്തള തവളാച്ചി’ കളികൾ എന്നും ഒരു പോസ്റ്റെഴുതി. പിന്നീടു മഷിത്തണ്ടിൽ വന്ന അത്തള പിത്തള തവളാച്ചിയും വിക്കിച്ചൊല്ലുകളിൽ ചേർക്കാനുള്ള അനൂപിന്റെ നിർദ്ദേശവും ഇതുപോലെയുള്ള വായ്ത്താരികൾ ധാരാളം നൽകി. എല്ലാവർക്കും നന്ദി.

ഡാലിയുടെ ആദ്യത്തെ പോസ്റ്റിനു് രണ്ടു മാസം മുമ്പു് എഴുതിയ പോസ്റ്റാണു് ഇതു്. ഡാലിയുടെ പോസ്റ്റുകളിലെയും അവയുടെ കമന്റുകളിലെയും വിവരങ്ങൾ ചേർത്തു് പോസ്റ്റ് അപ്‌ഡേറ്റ് ചെയ്യാം എന്നു കരുതി നീട്ടിവെച്ചു. ആ നീട്ടിവെയ്പ്പു് ഒന്നരക്കൊല്ലത്തിലധികം നീളും എന്നു കരുതിയില്ല.

ഇതിൽ ആദ്യം ചേർത്ത വായ്ത്താരികൾ കുറേപ്പേർക്കു് ഈമെയിലയച്ചു കിട്ടിയ മറുപടികളിൽ നിന്നാണു ശേഖരിച്ചതു്. ഇതിലെ വായ്ത്താരികള്‍ അയച്ചു തന്ന അനില്‍, കണ്ണൂസ്, കല്യാണി, തുളസി, ദില്‍ബാസുരന്‍, പച്ചാളം, ബിന്ദു, ബിരിയാണിക്കുട്ടി, മഞ്ജിത്ത്, രാജേഷ് വര്‍മ്മ, ശ്രീജിത്ത്, സന്തോഷ്, സിദ്ധാര്‍ത്ഥന്‍, സിബു എന്നിവര്‍ക്കു നന്ദി. (ഇവരൊക്കെ ഇതു മറന്നുപോയിട്ടുണ്ടാവും. 2007 ഫെബ്രുവരിയിലാണു സംഭവം!)

സൂക്ഷിച്ചു നോക്കിയാൽ ഈ കളിക്കുപയോഗിക്കുന്ന വായ്ത്താരികൾക്കെല്ലാം ഒരു പ്രത്യേകതയുണ്ടെന്നു കാണാം.

കുറേ കുട്ടികൾ തങ്ങളുടെ രണ്ടു കൈകളും (എണ്ണുന്ന ആൾ മാത്രം ഒരു കൈ) തറയിൽ കമഴ്ത്തി വെച്ചാണു കളി തുടങ്ങുക. ഏതെങ്കിലും ഒരു കൈയിൽ നിന്നു് എണ്ണിത്തുടങ്ങും. അവസാനത്തെ വാക്കു് നിൽക്കുന്ന കൈ മലർത്തിവെയ്ക്കും. മലർന്നിരിക്കുന്ന കൈയിലാണു വാക്കെത്തുന്നതെങ്കിൽ ആ കൈ കളിയിൽ നിന്നു മാറ്റും. അടുത്ത എണ്ണം തുടങ്ങുന്നതു് ആ കൈയുടെ പിന്നിലുള്ള കൈയിലാണു്. കളിയിൽ നിന്നു മാറിയ കൈകളെ പിന്നീടു കളിയിൽ ചേർക്കില്ല. അങ്ങനെ അവസാനം ഒരു കൈ ബാക്കി വരും.

ഈ കളി കളിച്ചിട്ടുള്ളവരെല്ലാം ഒരു കാര്യം ശ്രദ്ധിച്ചിട്ടുണ്ടായിരിക്കും. എല്ലാ കൈകളും മലർന്നതിനു ശേഷമേ സാധാരണയായി ഒരു കൈ കളിക്കു പുറത്തു പോകാറുള്ളൂ. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, എല്ലാ കൈകളും മലർക്കുന്നതു വരെ വായ്ത്താരി തീരുന്നതു് ഒരു കമഴ്ന്ന കൈയിൽ ആയിരിക്കും. കുട്ടികളുടെ(കൈകളുടെ) എണ്ണം എത്രയായാലും ഇതു മിക്കപ്പോഴും ശരിയായിരിക്കും.

ഈ പ്രത്യേകത മൂലം ഇത്തരത്തിലുള്ള വായ്ത്താരികൾ ഏകദേശം റാൻഡമായി, എന്നാൽ എല്ലാവർക്കും തുല്യമായ അവസരം കൊടുത്തു്, ഒരാളെ തിരഞ്ഞെടുക്കാനും ഉപയോഗിക്കാം. ഉദാഹരണമായി, ഒരു കൂട്ടായ്മയിൽ അടുത്ത പാട്ടു പാടേണ്ടതു് ആരാണെന്നു തീരുമാനിക്കാൻ. എല്ലാവരും പാടിക്കഴിഞ്ഞേ ആദ്യം പാടിയ ആൾക്കു വീണ്ടും അവസരം ലഭിക്കൂ.

ഇതെങ്ങനെ സംഭവിക്കുന്നു എന്നു് ആരെങ്കിലും ആലോചിച്ചിട്ടുണ്ടോ? ഇതിന്റെ ഉള്ളുകള്ളി മനസ്സിലാക്കാൻ അല്പം നമ്പർ തിയറിയുടെ സഹായം വേണ്ടി വരും.

ഇതു സംഭവിക്കുന്നതു് വായ്ത്താരിയിലെ വാക്കുകളുടെ എണ്ണവും കുട്ടികളുടെ എണ്ണവും തമ്മിൽ ആപേക്ഷിക-അഭാജ്യം (Relatively prime/Coprime) ആകുമ്പോഴാണു്.

ഉദാഹരണത്തിനു്, ഒരു വായ്ത്താരിയ്ക്കു് 9 വാക്കുകളുണ്ടെന്നിരിക്കട്ടേ. ഏഴു കുട്ടികൾ/കൈകൾ ഉള്ള ഒരു കളിയിൽ ആദ്യം രണ്ടാമത്തെ കൈ മലർക്കും. പിന്നെ 4, 6, 1, 3, 5, 7 എന്നീ കൈകളും. ഒമ്പതും ഏഴും ആപേക്ഷികമായി അഭാജ്യങ്ങളായതു കൊണ്ടാണു് ഇതു്. അതേ സമയം, ആറു കുട്ടികളേയുള്ളെങ്കിൽ 3, 6 എന്നീ കൈകൾ മലർന്നതിനു ശേഷം ബാക്കി കൈകൾ മലർത്തുന്നതിനു മുമ്പു് വീണ്ടും മൂന്നിൽത്തന്നെ എത്തും. ഒമ്പതും ആറും ആപേക്ഷികമായി അഭാജ്യങ്ങളല്ലാത്തതു കൊണ്ടാണു് (രണ്ടിനെയും 3 കൊണ്ടു ഹരിക്കാം.) ഇതു സംഭവിക്കുന്നതു്.

ഇനി, കുട്ടികളുടെ എണ്ണം എത്രയായാലും ഇതു സംഭവിക്കാൻ എന്താണു വഴി? മിക്കവാറും എല്ലാ സംഖ്യകളോടും ആപേക്ഷികമായി അഭാജ്യമായ ഒരു സംഖ്യ വായ്ത്താരികളുടെ എണ്ണമായി ഉപയോഗിച്ചാൽ മതി. അതിനു് ഏറ്റവും നല്ല വഴി ഒരു അഭാജ്യസംഖ്യ (Prime number) തന്നെ ഉപയോഗിക്കുന്നതാണു്.

പറഞ്ഞു വന്നതു്, അക്കുത്തിക്കുത്തുകളിക്കുപയോഗിക്കുന്ന എല്ലാ നല്ല വായ്ത്താരികൾക്കും ഉള്ള ഭാഗങ്ങളുടെ എണ്ണം അഭാജ്യസംഖ്യകൾ ആയിരിക്കും എന്നാണു്. അഭാജ്യസംഖ്യകൾ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53,… എന്നിങ്ങനെ പോകുന്നു. വായ്ത്താരികളിലെ ഖണ്ഡങ്ങളുടെ എണ്ണം ഇവയിൽ ഒരെണ്ണമായിരിക്കും.

വിശ്വസിക്കാൻ കഴിയുന്നില്ല, അല്ലേ? നമുക്കറിയാവുന്ന വായ്ത്താരികളൊക്കെ ഒന്നു പരിശോധിച്ചു നോക്കാം. നിർത്തുന്ന ഭാഗങ്ങൾ ഒരു വര (-) കൊണ്ടു കാണിച്ചിരിക്കുന്നു. ഖണ്ഡങ്ങളുടെ എണ്ണം ബ്രായ്ക്കറ്റിലും.

1. അത്തിള്‍-ഇത്തിള്‍-പറങ്കി-പ്പാള-ചട്ടുമ-ചിട്ടുമ-ചള്‍ (7)
2. അത്തിളി-മുത്തളി-പറങ്കീ-താളി-സെറ്റുമ്മ-സെറ്റുമ്മ-സാ (7)
   ഇതു മുകളില്‍ കൊടുത്തതു തന്നെയാണെന്നു തോന്നുന്നു.
3. അക്കു-ത്തിക്കു-ത്താനവ-രുമ്പം-
   കല്ലേ-ക്കുത്ത് ക-രിങ്കു-ത്ത്-
   അക്കര-നിക്കണ-ചക്കി-പ്പെണ്ണിന്റെ-
   കയ്യോ-കാലോ-അടിച്ചൊ-ടിച്ച് -വാ. (17)
4. അക്കു-ത്തിക്കു-ത്താന വ-രമ്പേല്‍-
   കല്ലേ-ക്കുത്തു ക-ടുംകു-ത്ത്‌
   ചീപ്പു-വെള്ളം-താറാ-വെള്ളം-
   താറാ-മ്മക്കടെ-കയ്യേ-ലൊരു-
   വാങ്ക്‌ (17)
5. അത്തള-പിത്തള-തവളാ-ച്ചി-
   മുക്കിലി-രിക്കണ -ചൂലാ-പ്പ്‌-
   മറിയം-വന്ന് വി-ളക്കൂ-തി
   ഉണ്ടോ-മാണി-സാറാ-പീറാ-കോട്ട്‌. (17)
6. അരിപ്പോ-തിരിപ്പോ-
   പന്ത്ര-ണ്ടാനേം-
   ചക്കിട്ട-പൊക്കിട്ട-
   പതിനാം-വള്ളികെ-ന്തൂമ്പു?-
   മുരിക്കിന്‍ -പു (11)
7. മുരിക്കീലൊ-രിക്കി കെ-ടന്നോ-നെ-
   കൊങ്ങാ-യെണ്ണ കു-ടിച്ചോ-നെ-
   അത്തര-മുള്ളൊരു -മാട-പ്രാ-വിന്റെ-
   കയ്യൊ-കാലോ-ചെത്തി-കൂട്ട് മ-ടംകൂ-ട്ട് (19)
8. പരിപ്പു -കുത്തി- പാച്ചോ-റാക്കി
   ഞാനു-മുണ്ട് -സീതേ-മുണ്ട് –
   സീ‍തേ-ടപ്പന്റെ- പേരെന്ത് (11)
9. inki -pinki -ponki-
   uncle -has a -donkey-
   donkey – died -uncle – cried-
   inki -pinki -ponki (13)
10. uncle – called the – doctor
    doctor -called the – nurse
    nusre – called the – ambu – lance
    A – B – C (13)
11. Eena, – meena, – mina, – mo, –
    Catch a – tiger – by his – toe. –
    If – he – squeals, – let ‘im – go, –
    Eena, – meena, – mina, – mo. (17)

    ഈ പാട്ടിനു് അതിഭീകരമായ ഒരു ചരിത്രമുണ്ടു്.

    Eena, meena, mina, mo,
    Catch a nigger by his toe;
    If he squeals, let him go,
    Eena, meena, mina, moe

    എന്നായിരുന്നു ഇതിന്റെ ആദ്യത്തെ രൂപം.

12. Ring – around the – ro – sey-
    A pocket – full of – po – sies –
    Ashes, – ashes –
    We all – fall – down (13)
13. അഡുപ്പും – തിഡുപ്പും –
    പാദര-പ്പള്ളില്‍-
    ബാങ്ക്‌ – കൊടുക്കും –
    ഏനുപ്പു? (7)
14. ഞാ-നൊ-രു-മ-നു-ഷ്യ-നെ- ക-ണ്ടു
    അ-യാ-ളു-ടെ-നി-റം-എ-ന്ത്?
    പ-ച്ച. (17)
15. ഒന്ന്, – രണ്ട്, – മൂന്ന്, – നാല് –
    അഞ്ച്, – ആറു്, – ഏഴ്, – എട്ട് –
    എട്ടും – മുട്ടും – താമര – മൊട്ടും –
    വടക്കോ-ട്ടുള്ള – അച്ഛനു-മമ്മയും
    പൊ-ക്കോ-ട്ടെ. (19)
16. അത്തിള്‍ – ഇത്തിള്‍ – ബെന്തി-പ്പൂ
    സ്വര്‍ഗ – രാജാ – പിച്ചി-പ്പൂ
    ബ്ലാം – ബ്ലീം – ബ്ലൂം (11)
17. അരിപ്പോ – തിരിപ്പോ – തോരണി – മംഗലം –
    പരിപ്പൂ – പന്ത്ര – ണ്ടാനേം – കുതിരേം –
    കുളിച്ച് – ജപിച്ച് – വരുമ്പം –
    എന്തമ്പൂ? മുരിക്കുമ്പൂ! (13)
18. മുരിക്കി – ചെരിക്കി – കെടന്നോ – ളേ
    അണ്ണാ-യെണ്ണ കു-ടിച്ചോ – ളേ
    അക്കര – നിക്കണ – മാട – പ്രാവിന്റെ –
    കയ്യോ – കാ‍ലോ – രണ്ടാ – ലൊന്ന് –
    കൊത്തി – ച്ചെത്തി –
    മടം കാട്ട് (19)
19. അരിപ്പ – തരിപ്പ – താലി – മംഗലം –
    പരിപ്പു – കുത്തി – പഞ്ചാ -രെട്ട്
    ഞാനു – മെന്റെ – ചിങ്കിരി – പാപ്പന്റെ
    പേരെന്ത്??? (13)

അക്കുത്തിക്കുത്തുകളിയിൽ ഓരോരുത്തരായി പുറത്തായി അവസാനം ശേഷിക്കുന്ന ആൾ ജയിക്കുമല്ലോ. എവിടെ നിന്നാൽ ഈ അവസാനത്തെ ആൾ ആകാം എന്നു മുൻ‌കൂട്ടി അറിയാമെങ്കിൽ എപ്പോഴും ജയിക്കാമല്ലോ. അതിനു് എന്തെങ്കിലും വഴിയുണ്ടോ?

വാക്കുകളുടെ എണ്ണം 2 ആയാലുള്ള (അതായതു്, ഒന്നിടവിട്ട ആളുകളെ ഒഴിവാക്കിയാൽ) സ്ഥിതിയെപ്പറ്റി ധാരാളം പഠനങ്ങൾ ഉണ്ടായിട്ടുണ്ടു്. കുട്ടികളുടെ എണ്ണം 1, 2, 3, 4, …. എന്നിങ്ങനെ ആയാൽ അവസാനം അവശേഷിക്കുന്ന കുട്ടിയുടെ നമ്പർ (ഇവിടെ ഒന്നു തൊട്ടാണു് എണ്ണുന്നതു്) 1, 1, 3, 1, 3, 5, 1, 3, 5, 7, 1, 3, 5, 7, 9, …. എന്നിങ്ങനെ ആയിരിക്കും.

ഇതു കണ്ടുപിടിക്കാൻ മറ്റൊരു എളുപ്പവഴിയുണ്ടു്. കുട്ടികളുടെ എണ്ണത്തെ ദ്വയാങ്കരീതിയിൽ (binary system) എഴുതുക. അങ്ങനെ കിട്ടുന്ന ബിറ്റുകളെ ഇടത്തേയ്ക്കു് ഒരു സ്ഥാനം ചാക്രികമായി നീക്കുക (cyclic bit shift). കിട്ടുന്ന സംഖ്യയായിരിക്കും ഒടുക്കം വരുന്ന കുട്ടിയുടെ നമ്പർ.

ഉദാഹരണമായി, നമ്മുടെ വായ്ത്താരി “അടി, ഇടി” എന്നാണെന്നിരിക്കട്ടേ. “ഇടി” എന്നു പറഞ്ഞു തൊടുന്ന ആൾ പുറത്താകും. ഈ കളി പതിനായിരം കുട്ടികൾ കളിച്ചാൽ ആരു് അവസാനം അവശേഷിക്കും?

10000 എന്ന സംഖ്യ ബൈനറിയിൽ എഴുതിയാൽ 10011100010000. ഇടത്തേയ്ക്കു് ഒരു സ്ഥാനം സൈക്ലിക് ബിറ്റ്-ഷിഫ്റ്റ് നടത്തിയാൽ ഏറ്റവും ഇടത്തേ 1 ഏറ്റവും വലത്തു പോകും. അതായതു് 00111000100001 അഥവാ 111000100001. ഇതു് 3617 എന്ന ദശാംശസംഖ്യയ്ക്കു തുല്യമായ ദ്വയാങ്കസംഖ്യയാണു്. അതായതു് ഈ കളിയിൽ 3617-)ം സ്ഥാനത്തു നിൽക്കുന്ന കുട്ടിയായിരിക്കും ജയിക്കുക.

വായ്ത്താരിയിലെ വാക്കുകളുടെ എണ്ണം എത്രയായാലും ഇതു കണക്കുകൂട്ടാൻ ഇതുപോലെ സരളമായ ഒരു രീതി ഇതു വരെ ആരും കണ്ടുപിടിച്ചിട്ടില്ല.

കുട്ടികളുടെ എണ്ണം k എന്നും വായ്ത്താരിയിലെ വാക്കുകളുടെ എണ്ണം v എന്നും ഇരിക്കട്ടേ. അപ്പോൾ ഒന്നു തൊട്ടെണ്ണിയാൽ 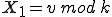എന്ന കുട്ടി ആദ്യം പുറത്താകും. എന്ന കുട്ടി രണ്ടാമതും. ഇങ്ങനെ അവശേഷിക്കുന്ന ആളെയാണു് കണ്ടുപിടിക്കേണ്ടതു്. നമുക്കു് അയാളുടെ നമ്പറിനെ എന്നു വിളിക്കാം.

ഇതു കണ്ടുപിടിക്കാനുള്ള സൂത്രവാക്യം (formula) ഒന്നും ആരും ഇതുവരെ കണ്ടുപിടിച്ചിട്ടില്ല. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, constant time algorithms ഒന്നുമില്ല.

നമ്മൾ സാധാരണ ചെയ്യുന്നതുപോലെ ചെയ്തുനോക്കാം. എണ്ണിത്തന്നെ. എണ്ണി ഓരോരുത്തരെ ഒഴിവാക്കുന്നതിനു പകരം ഓരോ റൌണ്ടിലും ഒഴിവാക്കേണ്ടവരെ ഒന്നിച്ചു് ഒഴിവാക്കിയിട്ടു് (ഉദാഹരണമായി, v = 11 ആണെങ്കിൽ, 11, 22, 33, … എന്നീ നമ്പരുകാരെ ഒന്നിച്ചു് ഒഴിവാക്കുക.) അതിനു ശേഷം എല്ലാവർക്കും പുതിയ നമ്പരുകൾ കൊടുക്കുക. ഇതു് O(v.(log k)) സമയത്തിനുള്ളിൽ ചെയ്യാം. കുട്ടികളുടെ എണ്ണം കൂടുതലാണെങ്കിൽ ഇതുതന്നെ ഏറ്റവും എളുപ്പമുള്ള വഴി.

കുട്ടികളുടെ എണ്ണം കുറവും വാക്കുകളുടെ എണ്ണം കൂടുതലുമാണെങ്കിൽ O(k) സങ്കീർണ്ണതയുള്ള ഒരു അൽഗരിതം ഉണ്ടു്. താഴെക്കൊടുക്കുന്ന ആവർത്തക-ഏകദം (recurrence relation) ഉപയോഗിച്ചു ക്രമമായി കണക്കുകൂട്ടുന്നതു്.

ഇവിടെ കുട്ടികളെ 0, 1, …, (k-1) എന്നു് എണ്ണണം.

ഉദാഹരണമായി, വായ്ത്താരിയിലെ വാക്കുകളുടെ എണ്ണം 11 ആണെന്നിരിക്കട്ടേ. അതായതു്, v = 11.

എന്നിങ്ങനെ. അതായതു് 6 കുട്ടികൾ ഉണ്ടെങ്കിൽ തുടങ്ങുന്ന കുട്ടി മുതൽ നാലാമതു് (3 എന്നാണു് മുകളിൽ ഉത്തരം. പക്ഷേ നമ്മൾ പൂജ്യത്തിൽ നിന്നാണു് എണ്ണൽ തുടങ്ങുന്നതു് എന്നു് ഓർക്കുക.) നിൽക്കുന്ന ആളായിരിക്കും ജയിക്കുക എന്നർത്ഥം. ഒരേ വായ്ത്താരി തന്നെയാണു നമ്മൾ എപ്പോഴും ഉപയോഗിക്കുന്നതെങ്കിൽ അതിന്റെ പട്ടിക നേരത്തേ ഉണ്ടാക്കി അതിനനുസരിച്ചു നിന്നു് എപ്പോഴും ജയിക്കാം.

ജോസഫസ് പ്രശ്നം (Josephus Problem) എന്നാണു് ഇതിനെ വിളിക്കുന്നതു്. ക്രിസ്തുവിനു ശേഷം ഒന്നാം നൂറ്റാണ്ടിൽ ജീവിച്ചിരുന്ന ഫ്ലേവിയസ് ജോസഫസ് എന്ന ജൂതചരിത്രകാരനുമായി ബന്ധപ്പെട്ട ഒരു കഥയിൽ നിന്നാണു് ഈ പേരുണ്ടായതു്. അന്നു റോമക്കാർ ജൂതന്മാരെ കൂട്ടമായി വേട്ടയാടുന്ന കാലമാണു്. ജോസഫസ് ഉൾപ്പെടെ 41 പേർ ഒരു ഗുഹയിൽ പെട്ടുപോയി. ചുറ്റും റോമൻ പട്ടാളവും. കീഴടങ്ങലിനേക്കാൾ ഭേദം ആത്മഹത്യയാണെന്നു തീരുമാനിച്ച ജൂതർ ഒരു വൃത്തത്തിൽ നിൽക്കാനും ജീവനോടെ നിൽക്കുന്ന ഓരോ മൂന്നാമത്തെ ആളെയും ബാക്കിയുള്ളവർ ചേർന്നു കൊല്ലാനും തീരുമാനിച്ചു. എങ്ങനെയെങ്കിലും രക്ഷപ്പെടണമെന്നുണ്ടായിരുന്ന ജോസഫസ് തന്റെ ഗണിതശാസ്ത്രപാടവം കൊണ്ടു് അവസാനം വരുന്ന ആൾ മുപ്പത്തൊന്നാമനായിരിക്കും എന്നു കണക്കുകൂട്ടി അവിടെ ആദ്യം തന്നെ ചെന്നു നിന്നു് മരണത്തിൽ നിന്നു രക്ഷപ്പെട്ടു എന്നാണു് ഐതിഹ്യം.

കണ്ടോ ഗണിതശാസ്ത്രത്തിന്റെ മാഹാത്മ്യം! ചുമ്മാതാണോ ആടുതോമയുടെ അച്ഛൻ തിലകൻ പറഞ്ഞതു് ലോകം മുഴുവൻ മാത്തമാറ്റിക്സാണെന്നു്!

ജോസഫസ് പ്രശ്നത്തെപ്പറ്റി കൂടുതലറിയാൻ വിക്കിപീഡിയയോ വൂൾഫ്രം മാത്ത് വേൾഡോ വായിക്കുക.

19 വാക്കുകളുള്ള ഒരു വായ്ത്താരിയുപയോഗിച്ചൂ് പതിനായിരം കുട്ടികൾ അത്തള പിത്തള തവളാച്ചി കളിച്ചാൽ അവസാനം ആരു ജയിക്കും എന്നു മുൻ‌കൂട്ടി പറയാൻ കമ്പ്യൂട്ടർ ഉപയോഗിക്കാതെ ഇന്നും ബുദ്ധിമുട്ടാണെന്നു ചുരുക്കം. ഗണിതശാസ്ത്രത്തിൽ കണ്ടുപിടിക്കാത്ത അനേകം കാര്യങ്ങൾ ഇനിയുമുണ്ടെന്നു മനസ്സിലായില്ലേ? നമ്മുടെ അത്തളപിത്തളക്കളി ആളു പുലിയാണെന്നും!

ഇതെങ്ങനെ ജോസഫസ് കണ്ടുപിടിച്ചു എന്നാണു് എന്റെ സംശയം. അങ്ങേർ 41 കല്ലുകൾ വട്ടത്തിൽ വെച്ചു് ഓരോന്നും എടുത്തുകളഞ്ഞു് ഏതു് അവസാനം വരും എന്നു കണ്ടുപിടിച്ചുകാണും. ഒരു പക്ഷേ, ഗണിതശാസ്ത്രം പരാജയപ്പെടുന്നിടത്തു് സിമുലേഷൻ ജയിക്കും എന്നതിന്റെ ആദ്യത്തെ ഉദാഹരണം ആവാം അതു്. കമ്പ്യൂട്ടറുകളുടെ പ്രചാരത്തോടെ ഇന്നു് പല പ്രശ്നങ്ങളും ഇങ്ങനെ ശുദ്ധഗണിതം ഉപയോഗിക്കാതെ സ്റ്റാറ്റിസ്റ്റിക്സും സിമുലേഷനും ഉപയോഗിച്ചു് നിർദ്ധരിക്കുന്നുണ്ടു്.

ഒരു തവണ ഒരാളെ ‘റാൻഡം’ ആയി കണ്ടുപിടിക്കാനും കുട്ടികൾ ഇതുപയോഗിക്കാറുണ്ടു്. (അമേരിക്കയിൽ “ഈനാ, മീനാ…” വായ്ത്താരിയാണു് ഇങ്ങനെ ഉപയോഗിക്കുന്നതു കണ്ടിട്ടുള്ളതു്.) ഇത്തരം ആവശ്യങ്ങൾക്കു് വായ്ത്താരികളുടെ എണ്ണം അഭാജ്യസംഖ്യയാകണമെന്നു നിർബന്ധമില്ല.

കൃത്യമായി ഒരു നിശ്ചിതസംഖ്യയ്ക്കു ശേഷം സംഭവിക്കുന്ന ഇതിനെ റാൻഡം എന്നു വിളിക്കാനും പറ്റില്ല. എങ്കിലും റാൻഡം നമ്പർ (റാൻഡം നമ്പറാഭാസം എന്നു പറയണം –pseudo-random number) ഉണ്ടാക്കാനുള്ള ഒരു വഴി ഈ അക്കുത്തിക്കുത്തുകളി തന്നെയാണെന്നതാണു സത്യം.

അക്കുത്തിക്കുത്തുകളിയിൽ ആളുകൾ പുറത്താകുന്നില്ല എന്നു കരുതുക. v വാക്കുകളും k കുട്ടികളും (0 മുതൽ k-1 വരെ നമ്പരുകൾ) ഉള്ള കളിയിൽ ഓരോ തവണയും ഏതു കുട്ടിയാണെന്നു നോക്കാം.

എന്നിങ്ങനെ. ചുരുക്കത്തിൽ

ഇതിനെ അല്പം കൂടി ഭേദപ്പെടുത്തിയാൽ, അതായതു് വലത്തുവശത്തെ ആദ്യത്തെ പദത്തെ ഒരു സ്ഥിരസംഖ്യ കൊണ്ടു ഗുണിച്ചാൽ, താഴെപ്പറയുന്ന രീതി കിട്ടും.

ഇതു തന്നെയാണു് മിക്കവാറും സോഫ്റ്റ്‌വെയറുകളിലും റാൻഡം നമ്പർ ഉണ്ടാക്കാൻ ഉപയോഗിക്കുന്ന ലീനിയർ കോൺഗ്ര്വെൻഷ്യൽ (Linear congruential) രീതി. a എന്ന സംഖ്യയ്ക്കു ചില പ്രത്യേകതകൾ ഉണ്ടെന്നു മാത്രം. സാധാരണയായി k, v എന്നിവ അഭാജ്യസംഖ്യകളായിരിക്കും.

അക്കുത്തിക്കുത്തു കളിക്കു് ഇത്രയധികം ഗണിതശാസ്ത്രപ്രാധാന്യമുണ്ടെന്നു് ആരെങ്കിലും കരുതിയോ?

ഇത്രയും പറഞ്ഞതിൽ‌നിന്നു് അക്കുത്തിക്കുത്തുകളിയുടെ വായ്ത്താരി ഉണ്ടാക്കിയവർക്കു് നമ്പർ തിയറിയിലെ മുകളിൽ പറഞ്ഞ സിദ്ധാന്തങ്ങൾ അറിവുണ്ടായിരുന്നു എന്നു പറയാൻ സാധിക്കുമോ? ആ സിദ്ധാന്തങ്ങൾ പ്രസ്താവിച്ചു തെളിയിച്ചവരല്ല, അക്കുത്തിക്കുത്തു വായ്ത്താരി പോലെയുള്ളവ ഉണ്ടാക്കിയവരാണു യഥാർത്ഥത്തിൽ ആ സിദ്ധാന്തങ്ങളുടെ ഉപജ്ഞാതാക്കൾ എന്നു പറയാൻ സാധിക്കുമോ?

സിദ്ധാന്തങ്ങളുടെ പൈതൃകത്തെപ്പറ്റിയുള്ള അവകാശവാദങ്ങൾ പലപ്പോഴും ഈ വിധത്തിലാണു് പോകുന്നതു്. അങ്ങനെയാണു് പിംഗളൻ ബൈനോമിയൽ തിയറം കണ്ടുപിടിക്കുന്നതും വേദങ്ങളിൽ കാൽക്കുലസ് ഉണ്ടാകുന്നതും വാല്മീകിയുടെ കാലത്തു വിമാനം കണ്ടുപിടിക്കുന്നതും മറ്റും.

അക്കുത്തിക്കുത്തുകളിയുടെ വായ്ത്താരി ഉണ്ടാക്കിയവർക്കു് തിരഞ്ഞെടുക്കപ്പെടുന്നവർ ആവർത്തിക്കാതെ കഴിയുന്നത്ര വിതരണം ചെയ്തു പോകണമെന്നുണ്ടായിരുന്നു. ചില എണ്ണങ്ങൾ ആവർത്തിക്കുന്നതും ചിലവ ആവർത്തിക്കാതിരിക്കുന്നതും അവർ ശ്രദ്ധിച്ചിട്ടുണ്ടാവാം. അങ്ങനെ പലതു ശ്രമിച്ചിട്ടാവാം ഇന്നു പ്രചാരത്തിലുള്ള വായ്ത്താരികൾ ഉണ്ടായതു്. അല്ലെങ്കിൽ, വായ്ത്താരികളിൽ നിന്നു് ഈ പ്രത്യേകത ഉള്ളവ മാത്രം പ്രചാരത്തിലായി എന്നുമാവാം. അവയ്ക്കും അഭാജ്യസംഖ്യകൾക്കും തമ്മിലുള്ള ബന്ധം ആരും ശ്രദ്ധിച്ചു കാണില്ല. അതുകൊണ്ടാണു് ആരും ഇതുവരെ അതിനെപ്പറ്റി എഴുതി വെയ്ക്കാഞ്ഞതു്.

മറിച്ചു്, സിദ്ധാന്തങ്ങളുണ്ടാക്കിയവർ അതു് ഒരു ദിവസം കൊണ്ടു് ഉണ്ടാക്കിയതല്ല. (ആപ്പിൾ തലയിൽ വീണപ്പോൾ പെട്ടെന്നു ബോധോദയം ഉണ്ടായി ന്യൂട്ടൻ ഗുരുത്വാകർഷണനിയമം ഉണ്ടാക്കി എന്ന കള്ളക്കഥയാണല്ലോ നമുക്കു കൂടുതൽ പരിചയം!) അക്കുത്തിക്കുത്തു കളികൾ പോലെ നാട്ടിൽ പ്രചരിക്കുന്ന പല കളികളുടെയും പ്രസ്താവനകളുടെയും പസിലുകളുടെയും ഉള്ളുകള്ളികളിലേയ്ക്കു ചുഴിഞ്ഞാലോചിച്ചവർ അവരുടെ നിരീക്ഷണങ്ങൾ എഴുതിവെയ്ക്കുകയും പിന്നീടു വന്നവർ അവയെപ്പറ്റി കൂടുതൽ പഠിച്ചു് സിദ്ധാന്തങ്ങളാക്കി തെളിയിക്കുകയും ചെയ്തതാവാം. നൂറ്റാണ്ടുകൾ നീണ്ടുനിന്ന ശാസ്ത്രവികാസത്തിന്റെ ക്രെഡിറ്റ് “അമ്പത്താറു്” കളിയിൽ അവസാനം വിളിച്ചുനിർത്തുന്നവൻ മാത്രം കുണുക്കിറക്കുന്നതു പോലെ അവസാനത്തെ കുരുക്കഴിച്ചവന്റെ പേരിൽ മാത്രം പതിയുന്നു എന്നു മാത്രം. കാൽക്കുലസ് കണ്ടുപിടിച്ച ന്യൂട്ടൻ/ലൈബ്നിറ്റ്സും ഫെർമയുടെ അന്ത്യസിദ്ധാന്തം തെളിയിച്ച വെയിൽ‌സും ഇതിനു് ഉദാഹരണങ്ങൾ മാത്രം.

ഞാൻ മലയാളം ബ്ലോഗിംഗു തുടങ്ങിയിട്ടു് നാലു വർഷം തികയുന്നു. 2005 ജനുവരി 19-നെഴുതിയ ആദ്യ പോസ്റ്റ്. ഇതു് ഇരുനൂറ്റിമുപ്പത്തേഴാമത്തെ പോസ്റ്റ്. അതായതു്, ഏകദേശം ആറു ദിവസത്തിൽ ഒരു പോസ്റ്റു വീതം. അനോണി ആന്റണി, ബെർലി, നമതു് തുടങ്ങിയവരെ അപേക്ഷിച്ചു നോക്കുമ്പോൾ ഒന്നുമല്ലെങ്കിലും ഇത്രയും നാൾ വലിയ മുടക്കമില്ലാതെ എഴുതാൻ കഴിഞ്ഞതിൽ സന്തോഷം.

ബ്ലോഗെഴുതാൻ മൂന്നു മണിക്കൂർ സമയം ഫ്രീ കിട്ടി. എന്തു ചെയ്യണം?

ഒരുപാടു കാലത്തിനു ശേഷമാണു് തടസ്സങ്ങളില്ലാതെ ഇത്രയും സമയം കിട്ടുന്നതു്. തിരക്കിനിടയിൽ വീണുകിട്ടുന്ന മിനിറ്റുകളിൽ എഴുതുന്ന തുണ്ടുകളെ ചേർത്തുവെച്ചാണു പലപ്പോഴും പോസ്റ്റുകളാക്കുന്നതു്. ഒരു ആശയം കിട്ടിയാൽ ഒരു പുതിയ പോസ്റ്റ് തുടങ്ങി ഒരു തലക്കെട്ടും കൊടുത്തു് രണ്ടു വാക്യങ്ങളും എഴുതി അവിടെയിടും. അല്പം സമയം കിട്ടുമ്പോൾ ഡ്രാഫ്റ്റ് പോസ്റ്റുകളുടെ തലക്കെട്ടു നോക്കി അന്നേരത്തെ മൂഡനുസരിച്ചു് തോന്നുന്ന ഒന്നിൽ കുറേക്കൂടി ചേർക്കും. ഇടയ്ക്കു് ഒരു അരമുക്കാൽ മണിക്കൂർ കിട്ടുകയും ഏതെങ്കിലും ഒരു പോസ്റ്റ് തീരാറായിരിക്കുകയും ചെയ്യുമ്പോഴാണു് അവസാനപണികൾ ചെയ്തു് അതു പൂർത്തിയാക്കി പ്രസിദ്ധീകരിക്കുന്നതു്. (ഈ പോസ്റ്റു പോലെയുള്ള വയറിളക്കങ്ങൾക്കു് ഇതു ബാധകമല്ല)

ചുരുക്കം പറഞ്ഞാൽ ബ്ലോഗെഴുത്തിനു് അനോണി ആന്റണി തരുന്ന പെരുമാറ്റച്ചട്ടങ്ങളിൽ ഒന്നു പോലും ഞാൻ പാലിക്കാറില്ല എന്നർത്ഥം. ചുമ്മാതല്ല പോസ്റ്റുകൾ ഉണ്ടാകാത്തതു്!

അതു പോട്ടേ. എനിക്കിന്നു മൂന്നു മണിക്കൂർ സമയമുണ്ടു്. എഴുതിത്തീരാറായ ഏതെങ്കിലും പോസ്റ്റ് തീർക്കണമെന്നുണ്ടു്. ഇവയിൽ ഏതു തീർക്കും?

2006 ജൂണിൽ എഴുതിത്തുടങ്ങിയ “വൃത്തനിർണ്ണയം” എന്ന മൾട്ടിമീഡിയ പോസ്റ്റ് മുതൽ മധുരാജിന്റെ ഈ കമന്റ് കണ്ടപ്പോൾ തോന്നിയ “ചിന്തയുടെ ഭാഷ” എന്ന പോസ്റ്റ് വരെ ഡ്രാഫ്റ്റ് ആയി കിടക്കുന്ന 56 പോസ്റ്റുകളിലെ പലതും കാലഹരണപ്പെട്ടതാണു്. എങ്കിലും ഒരു പത്തുനാല്പതെണ്ണമെങ്കിലും ഇന്നും പ്രസക്തിയുള്ളവയാണു്. അവയിൽ പത്തെണ്ണമെങ്കിലും മിക്കവാറും തീർന്നിരിക്കുന്നതുമാണു്. ഏതെടുക്കണമെന്നു് ഒരു ചിന്താക്കുഴപ്പം.

അഞ്ചു മിനിട്ടു മാത്രം കിട്ടുമ്പോൾ ഈ ചിന്താക്കുഴപ്പം ഉണ്ടാകാറില്ല. തിരഞ്ഞെടുക്കാൻ സമയമില്ല. ഏതെങ്കിലും ഒന്നെടുക്കും. കൂടുതൽ സമയമുള്ളപ്പോൾ തിരഞ്ഞെടുക്കാനാണു സമയം മുഴുവൻ പോകുക. ഇടയ്ക്കിടെ, “അയ്യോ, കിട്ടിയ സമയം വെയ്സ്റ്റാക്കരുതല്ലോ” എന്നു വ്യാകുലപ്പെടാൻ പോകുന്ന സമയം വേറെയും.

അതെന്താ അങ്ങനെ?