Gurukulam | ഗുരുകുലം

എന്റെ പിറന്നാളും കലണ്ടറും എന്ന പോസ്റ്റില്‍ സങ്കുചിതമനസ്കന്‍ ഇങ്ങനെ ഒരു കമന്റിട്ടു:

19, 38, 57 എന്നിങ്ങനെ 19ന്റെ ഗുണിതങ്ങള്‍ വരുന്ന പിറന്നാളിന്റെ അന്ന് ഡേറ്റ് ഓഫ് ബര്‍ത്തും നാളും ഒന്നായി വരും എന്ന കാര്യം അറിയാമോ?

പിന്നീടു ദേവനു മറുപടിയായി സങ്കുചിതന്‍ ഇതും പറഞ്ഞു:

അപ്പോള്‍ കഴിഞ്ഞ വര്‍ഷം -38 ആം ജന്മദിനം ജൂണ്‍ 16 നു തന്നെ ആയിരുന്നിരിക്കും.

19, 38, 57 തുടങ്ങിയ 19ന്റെ ഗുണിതങ്ങള്‍ വരുന്ന വര്‍ഷങ്ങളില്‍ ജന്മദിനവും പിറന്നാളും ഒന്നിച്ചു വരുമെന്നു സങ്കുചിതന്‍ പറഞ്ഞതു് ഏറെക്കുറെ ശരിയാണെങ്കിലും, ദേവന്റെ മുപ്പത്തെട്ടാമത്തെ പിറന്നാള്‍ 2007 ജൂണ്‍ 16-നായിരുന്നില്ല. “കിറുകൃത്യം സങ്കൂ” എന്നു ദേവന്‍ പറഞ്ഞതു ശരിയായിരുന്നില്ല്ല. 2007 ജൂലെ 13-നായിരുന്നു. ദേവനെപ്പോലെ ചുരുക്കം ചിലര്‍ക്കു് പിറന്നാളും ജന്മദിനവും ഒരിക്കലും ഒന്നിച്ചു വരില്ല.

ദേവന്‍ തുടര്‍ന്നു ചോദിക്കുന്നു:

ജന്മദിനം കണ്ടുപിടിക്കാനുള്ള എന്തെങ്കിലും സൂത്രം വച്ച് ചെയ്തതാണോ അതോ പരിചയമുള്ള ആരെങ്കിലും ഈ തീയതിയില്‍ ജനിച്ചവരാണോ?

ആ സൂത്രമാണു് ഇവിടെ പറയുന്നതു്.

---

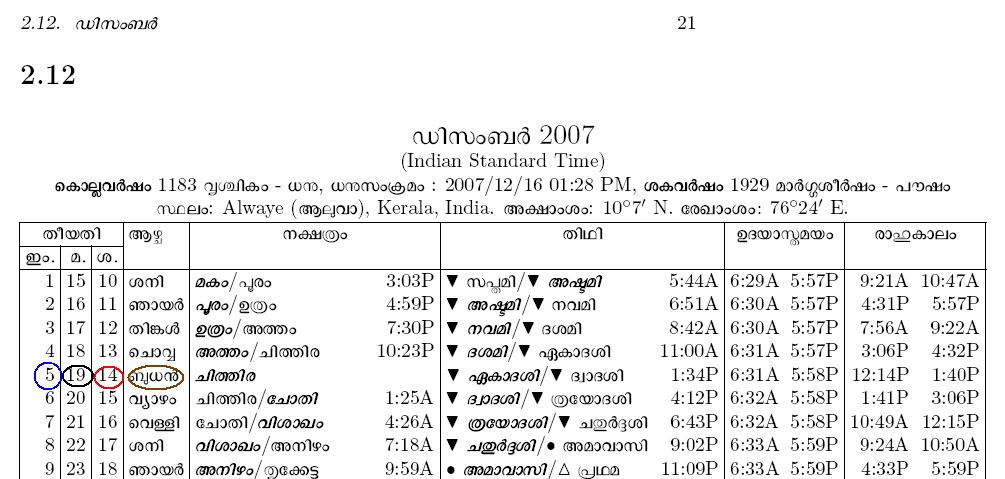
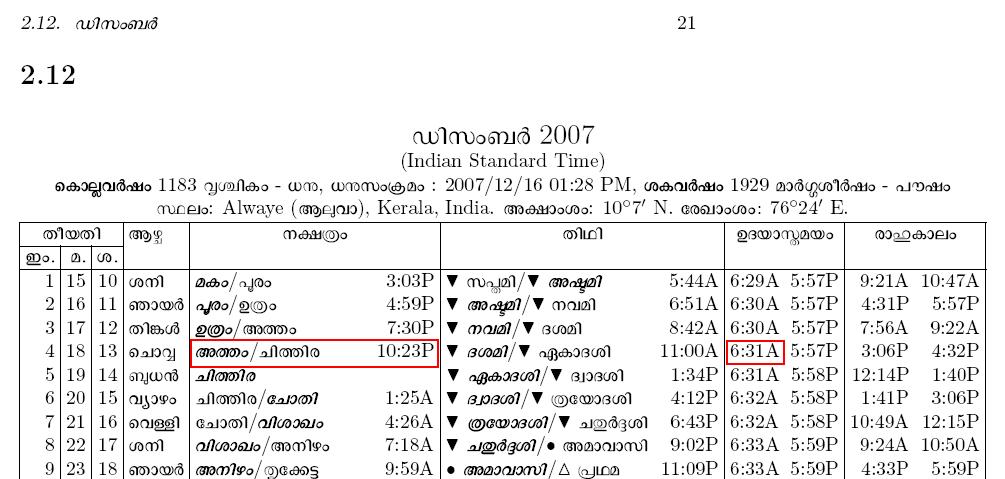
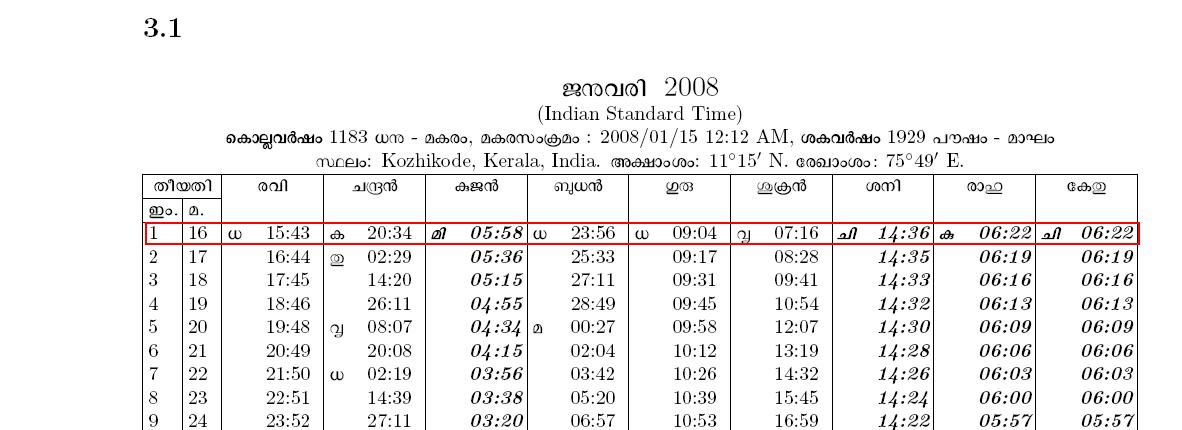
ഇതില്‍ പറയുന്ന എല്ലാ കണക്കുകളും കേരളത്തിലെ കണക്കനുസരിച്ചുള്ള കാലനിര്‍ണ്ണയത്തിന്റെ അടിസ്ഥാനത്തിലാണു്. ഉദാഹരണങ്ങള്‍ ആലുവയ്ക്കു വേണ്ടി ഞാനുണ്ടാക്കിയ കലണ്ടറില്‍ നിന്നും. മറ്റു സ്ഥലങ്ങളില്‍ അല്പം വ്യത്യാസങ്ങള്‍ വന്നേക്കാം.

അതു പോലെ, “ജന്മദിനം” എന്നതുകൊണ്ടു് ഇവിടെ വിവക്ഷിക്കുന്നതു് date of birth ആണു്. ഗ്രിഗോറിയന്‍ കലണ്ടറില്‍ ജനിച്ച മാസവും തീയതിയും എല്ലാ വര്‍ഷവും വരുന്ന തീയതി. “പിറന്നാള്‍” എന്നതു മലയാളം കലണ്ടറനുസരിച്ചു്, ജനിച്ച മലയാളമാസത്തിലെ ജന്മനക്ഷത്രം വരുന്ന ദിവസവും. ജന്മനക്ഷത്രം ഒരു മാസത്തില്‍ രണ്ടു തവണ വന്നാല്‍, രണ്ടാമത്തെ ദിവസമാണു പിറന്നാള്‍.

---

ജനിച്ച ദിവസം മുതല്‍ 19 വയസ്സു പൂര്‍ത്തിയാക്കുന്നതു വരെ 19 വര്‍ഷങ്ങള്‍ ഉണ്ടല്ലോ. അവയില്‍ അധിവര്‍ഷങ്ങളിലെ ഫെബ്രുവരി 29 നാലോ അഞ്ചോ തവണ വരാം. (ജനിച്ചതു് ഒരു ഫെബ്രുവരി 29 കഴിഞ്ഞു് ഒരു വര്‍ഷത്തിനുള്ളിലാണെങ്കില്‍ 4, അല്ലെങ്കില്‍ 5. അതായതു്, 365/1461 = 24.98% ആളുകള്‍ക്കു 4, ബാ‍ക്കിയുള്ള 75.02% ആളുകള്‍ക്കു് 5.)

അതായതു്, മുകളില്‍ പറഞ്ഞ 24.98% ആളുകള്‍ ജനിച്ചതിനു ശേഷം 365 x 19 + 4 = 6939 ദിവസത്തിനു ശേഷമാണു് പത്തൊന്‍പതാം ജന്മദിനം ആഘോഷിക്കുന്നതു്. ബാക്കി 75.02% ആളുകള്‍ 6940 ദിവസത്തിനു ശേഷവും.

ഇനി, ചന്ദ്രന്‍ ഭൂമിയ്ക്കു ചുറ്റും ഒരു തവണ കറങ്ങാന്‍ ശരാശരി 27.3217 ദിവസം എടുക്കും. (പ്രപഞ്ചത്തിലെ ഏതെങ്കിലും സ്ഥിരദിശയെ അടിസ്ഥാനമാക്കിയാണു് ഇതു്. സൂര്യനെ അടിസ്ഥാനമാക്കിയാണെങ്കില്‍ ഇതു് 29.5307 ദിവസമാണു്. കൂടുതല്‍ വിവരങ്ങള്‍ താഴെ.) ഈ സമയം കൊണ്ടാണു് അതേ നാള്‍ തന്നെ വീണ്ടും വരുന്നതു്.

19 വര്‍ഷത്തിലുള്ള ദിവസങ്ങളുടെ എണ്ണമായ 6940 ഏകദേശം 27.3217-ന്റെ ഗുണിതമാണു്. 254 x 27.3217 = 6939.7118. അതുകൊണ്ടാണു് ജന്മദിനവും പിറന്നാളും 19 വര്‍ഷത്തില്‍ ഒന്നിയ്ക്കുന്നതു്. എങ്കിലും 24.98% ആളുകള്‍ക്കു് മിക്കവാറും ഒരു ദിവസത്തെ വ്യത്യാസം ഉണ്ടാവും.

6940 – 6939.7118 = 0.2882 ദിവസമാണു് 19 വര്‍ഷം കൊണ്ടു് ഉണ്ടാകുന്നതു്. 38, 57, 76, 95 വര്‍ഷങ്ങളില്‍ ഇതു് യഥാക്രമം 0.5764, 0.8646, 1.1528, 1.441 ദിവസങ്ങളാണു്. അതായതു്, ഇവ തമ്മില്‍ ഒന്നിക്കാനുള്ള സാദ്ധ്യത കുറഞ്ഞുവരുന്നു എന്നര്‍ത്ഥം.

---

കലണ്ടര്‍ നിര്‍മ്മിച്ച മിക്കവാറും എല്ലാവരും തന്നെ ഈ 19 വര്‍ഷത്തിന്റെ പ്രത്യേകത കണ്ടിരുന്നു. പക്ഷേ മുകളില്‍ പറഞ്ഞതല്ല എന്നു മാത്രം. ഒരു സ്ഥിരദിശയെ അവലംബിച്ചുള്ള വ്യതിയാനം ശ്രദ്ധിക്കാന്‍ ബുദ്ധിമുട്ടാണു്.

പാശ്ചാത്യര്‍ ശ്രദ്ധിച്ചതു മറ്റൊരു യോജിപ്പാണു്. രണ്ടു കറുത്ത വാവുകള്‍ക്കിടയിലുള്ള സമയം 29.5307 ദിവസമാണു്.

ഭൂമി സൂര്യനു ചുറ്റും കറങ്ങുന്നതു കൊണ്ടാണു് ഇതു്. ചന്ദ്രന്‍ ഒരു തവണ ചുറ്റി വരുമ്പോഴേയ്ക്കും ഭൂമി കുറേ പോയിട്ടുണ്ടാവും. വര്‍ഷത്തിന്റെ ദൈര്‍ഘ്യം 365.242191 ആയതിനാല്‍ ഇതു കണ്ടുപിടിക്കാന്‍ എളുപ്പമാണു്.

ഇതാണു് ഒരു തിഥിചക്രം. ഈ കാലയളവാണു ചാന്ദ്രമാസം. ഇതിന്റെ അടിസ്ഥാനത്തിലാണു് മാസം എന്ന (30 ദിവസം) ആശയം ഉണ്ടായതു്. ഇസ്ലാമിക് കലണ്ടര്‍ ഇപ്പോഴും 12 ചാന്ദ്രമാസങ്ങളടങ്ങിയ വര്‍ഷമാണു് ഉപയോഗിക്കുന്നതു്. പ്രാചീനഭാരതീയകലണ്ടറുകളിലെയും മാസങ്ങള്‍ ചാന്ദ്രമാസങ്ങളായിരുന്നു.

6940 ദിവസങ്ങള്‍ ഇതിന്റെയും ഒരു ഏകദേശഗുണിതമാണു്. 235 x 29.5307 = 6939.688. ഇതാണു ഭൂരിപക്ഷം കലണ്ടര്‍‌നിര്‍മ്മാതാക്കളും ശ്രദ്ധിച്ച Metonic cycle. ഇവ രണ്ടും ഒരുപോലെ വന്നതു തികച്ചും യാദൃച്ഛികം.

സത്യം പറഞ്ഞാല്‍ അതു യാദൃച്ഛികമല്ല. ചന്ദ്രന്‍ ഭൂമിക്കു ചുറ്റും ഏകദേശം 12 തവണ ചുറ്റുമ്പോള്‍ ഭൂമി സൂര്യനെ ഏകദേശം ഒരു തവണ ചുറ്റുന്നതുകൊണ്ടു് 12 x 29.5307 = 354.3684 എന്നതും 13 x 27.3217 = 355.1821 എന്നതും വളരെ അടുത്തു വരുന്നതു കൊണ്ടു് നക്ഷത്രചക്രവും തിഥിചക്രവും ഓരോ വര്‍ഷത്തിലും ഏതാണ്ടു് അടുത്തു വരുന്നുണ്ടു്. ഓണം എന്നും പൌര്‍ണ്ണമിയ്ക്കടുത്തു വരുന്നതു പലരും ശ്രദ്ധിച്ചിരിക്കും. അതുപോലെ പിറന്നാളുകളും ഒരു പ്രത്യേക തിഥിയ്കായിരിക്കും എല്ലാ വര്‍ഷവും. 19 വര്‍ഷങ്ങള്‍ കൊണ്ടു് 6939.7118 – 6939.688 = 0.0238 ദിവസത്തിന്റെ വ്യത്യാസമേ നക്ഷത്രചക്രവും തിഥിചക്രവും തമ്മില്‍ ഉണ്ടാകുന്നുള്ളൂ. അതുകൊണ്ടാണു രണ്ടും ശരിയായതു്.

ഇത്രയും പറഞ്ഞതു്, 19 വര്‍ഷത്തിന്റെ Metonic cycle പലയിടത്തും കാണാം. ഉദാഹരണമായി വിക്കിപീഡിയയില്‍. അതു കൊണ്ടാണു് 19 വര്‍ഷത്തിലൊരിക്കല്‍ നാളും ജന്മദിനവും ഒന്നിക്കുന്നതെന്നു ചിലര്‍ ധരിച്ചിട്ടുണ്ടു്. അതു തെറ്റാണു്.

---

ചന്ദ്രന്‍ ഭൂമിക്കു ചുറ്റും കറങ്ങുന്നതു ന്യൂ ഇയറിന്റെ തലേ രാത്രിയില്‍ മഴനൂലുകള്‍ നടക്കുന്നതുപോലെയാണു്. അത്ര ക്രമത്തിലൊന്നുമല്ല എന്നര്‍ത്ഥം. അത്ര കൃത്യമായി കണക്കുകൂട്ടേണ്ട ആവശ്യം നമുക്കില്ല. ശരാശരി 27.3217 ദിവസം കൊണ്ടാണു് ചന്ദ്രന്‍ ഭൂമിയ്ക്കു ചുറ്റും കറങ്ങുന്നതു്. അതു് ഒരു ക്രമത്തിലാണെന്നു കരുതിയാല്‍ (കല്യാണത്തിനു ശേഷം മഴനൂലുകള്‍ അങ്ങനെയാണെന്നാണു കേള്‍ക്കുന്നതു്) ഒരു നക്ഷത്രത്തിന്റെ ദൈര്‍ഘ്യം 27.3217/27 = 1.01191 ദിവസമാണെന്നു കാണാം. മറ്റൊരു വിധത്തില്‍ പറഞ്ഞാല്‍, ഒരു ദിവസത്തില്‍ ശരാശരി 27/27.3217 = 0.988225476 നക്ഷത്രം മാറും. ഇതില്‍ നിന്നു് നമുക്കു് ഓരോ ജന്മദിനത്തിലെയും നക്ഷത്രം കണ്ടുപിടിക്കാമോ എന്നു നോക്കാം.

ആദ്യത്തെ പടി, ഓരോ ജന്മദിനവും എത്ര ദിവസത്തിനു ശേഷമാണു് എന്നറിയണം. ഒരു വര്‍ഷത്തിന്റെ ദൈര്‍ഘ്യം ഏകദേശം 365.25 ദിവസം ആണെങ്കിലും അങ്ങനെയല്ലല്ലോ വര്‍ഷത്തിന്റെ കിടപ്പു്. മൂന്നു തവണ 365 ദിവസവും നാലാമത്തെ വര്‍ഷം 366 ദിവസവുമാണു് ഒരു വര്‍ഷത്തിന്റെ ദൈര്‍ഘ്യം.

ഇതു പൂര്‍ണ്ണമായി ശരിയല്ല. എങ്കിലും 1901 മുതല്‍ 2099 വരെ ഇതു ശരിയാണു്. ഇതു വായിക്കുന്ന ആരും ഈ കാലയളവിനു വെളിയില്‍ ജന്മദിനം ആഘോഷിക്കാന്‍ സാദ്ധ്യതയില്ലാത്തതു കൊണ്ടു് നമുക്കു് ഇത്രയും ആലോചിച്ചാല്‍ മതി. ഗ്രിഗോറിയന്‍ കലണ്ടറിന്റെ വിശദവിവരങ്ങള്‍ക്കു് എന്റെ ഗ്രിഗോറിയന്‍ കലണ്ടര്‍ എന്ന പോസ്റ്റു വായിക്കുക.

ഇതു മൂലം ജന്മദിനത്തിനും വ്യത്യാസമുണ്ടാവും. 2006 ജൂണ്‍ 1-നു ജനിച്ച ഒരു കുഞ്ഞു് 365 ദിവസത്തിനു ശേഷം 2007 ജൂണ്‍ 1-നു് ഒന്നാം ജന്മദിനം ആഘോഷിക്കുമ്പോള്‍ (അതു് ഒന്നാമത്തേതോ രണ്ടാമത്തേതോ എന്ന പഴയ പ്രഹേളിക നമുക്കു തത്ക്കാലം മറക്കാം.) 2008-നു രണ്ടാം ജന്മദിനം ആഘോഷിക്കുന്നതു് പിന്നെ 366 ദിവസങ്ങള്‍ക്കു ശേഷമാണു്. (2008-ല്‍ ഫെബ്രുവരിയ്ക്കു് 29 ദിവസങ്ങളുണ്ടു്). കൃത്യമായ അന്തരാളത്തിലല്ല നാം ജന്മദിനം ആഘോഷിക്കുന്നതു് എന്നര്‍ത്ഥം.

ഇതില്‍ നിന്നു് നാലുതരം വര്‍ഷങ്ങള്‍ക്കു് (അധിവര്‍ഷം, അധിവര്‍ഷം+1, അധിവര്‍ഷം+2, അധിവര്‍ഷം+3) നാലു തരത്തിലാണു കണക്കുകൂട്ടേണ്ടതു് എന്നു കാണാം.

വര്‍ഷം	4k	4k+1	4k+2	4k+3
1	1 x 365	1 x 365	1x 365	1 x 365 + 1
2	2 x 365	2 x 365	2 x 365 + 1	2 x 365 + 1
3	3 x 365	3 x 365 + 1	3 x 365 + 1	3 x 365 + 1
4	4 x 365 + 1	4 x 365 + 1	4 x 365 + 1	4 x 365 + 1
5	5 x 365 + 1	5 x 365 + 1	5 x 365 + 1	5 x 365 + 2
6	6 x 365 + 1	6 x 365 + 1	6 x 365 + 2	6 x 365 + 2
7	7 x 365 + 1	7 x 365 + 2	7 x 365 + 2	7 x 365 + 2
8	8 x 365 + 2	8 x 365 + 2	8 x 365 + 2	8 x 365 + 2
9	9 x 365 + 2	9 x 365 + 2	9 x 365 + 2	9 x 365 + 3
10	10 x 365 + 2	10 x 365 + 2	10 x 365 + 3	10 x 365 + 3
…	…	…	…	…
n

-നേക്കാള്‍ ചെറിയ ഏറ്റവും വലിയ പൂര്‍ണ്ണസംഖ്യയെയാണു് എന്നതു കൊണ്ടു് ഉദ്ദേശിക്കുന്നതു്. ഉദാ:

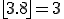
ചുരുക്കം പറഞ്ഞാല്‍, ഒരു വര്‍ഷം (4k+j) എന്ന രൂപത്തിലാണെങ്കില്‍ (k ഒരു പൂര്‍ണ്ണസംഖ്യ, j=0, 1, 2 or 3), n വര്‍ഷങ്ങള്‍ക്കു ശേഷമുള്ള ജന്മദിനം

ദിവസങ്ങള്‍ക്കു ശേഷമാണെന്നു കാണാം.

നമുക്കിനി ഒരുദാഹരണം നോക്കാം. 1969 ജൂണ്‍ 16-നു ജനിച്ച ദേവന്‍ 2008 ജൂണ്‍ 16-നു മുപ്പത്തൊമ്പതാം ജന്മദിനം ആഘോഷിക്കുന്നതു് എത്ര ദിവസങ്ങള്‍ക്കു ശേഷമാണു്?

1969 = 4 x 492 + 1 ആയതുകൊണ്ടു് മുകളില്‍ j = 1. അതുപോലെ n = 39. അപ്പോള്‍

ദിവസങ്ങള്‍ക്കു ശേഷമാണു ബഡ്വൈസനെ പൊട്ടിക്കുന്നതു്.

ജന്മദിനം ജനുവരിയിലോ ഫെബ്രുവരിയിലോ ആണെങ്കില്‍ ഇതിനു് അല്പം വ്യത്യാസമുണ്ടു്. അവര്‍ക്കു് ഒരു വര്‍ഷം നേരത്തേ അധിവര്‍ഷം വരും. ഏറ്റവും എളുപ്പമുള്ള വഴി അവരെ തലേ വര്‍ഷത്തിന്റെ ഭാഗമായി കൂട്ടുന്നതാണു്.

ഉദാഹരണമായി, 1972 ജനുവരി 10-നു ജനിച്ച സന്തോഷ് 2008 ജനുവരി 10-നു മുപ്പത്താറാം ജന്മദിനത്തില്‍ പൂര്‍ത്തിയാക്കിയ ദിവസങ്ങള്‍ കാണാന്‍ വേണ്ടി ജനിച്ച വര്‍ഷം തത്ക്കാലത്തേയ്ക്കു് 1971 എന്നു കരുതുക. 1971 = 4 x 492 + 3 ആയതിനാല്‍ j = 3. ഉത്തരം

ദിവസങ്ങള്‍.

അപ്പോള്‍ ഒരു പ്രത്യേകജന്മദിനത്തിനു് എത്ര ദിവസങ്ങള്‍ കഴിഞ്ഞു എന്നു കണക്കുകൂട്ടാന്‍ നമ്മള്‍ പഠിച്ചു. ഇനി, ഒരു ദിവസത്തില്‍ ശരാശരി 27/27.3217 = 0.988225476 നക്ഷത്രം മാറും എന്നും നമ്മള്‍ കണ്ടു. അപ്പോള്‍ അത്ര ദിവസം കൊണ്ടു് എത്ര നാളുകള്‍ കഴിഞ്ഞു എന്നു കണക്കുകൂട്ടാന്‍ ബുദ്ധിമുട്ടില്ല.

ഒരു ഉദാഹരണം ശ്രദ്ധിച്ചാല്‍ എളുപ്പമാകുമെന്നു തോന്നുന്നു. 1965 നവംബര്‍ 22-നു വൃശ്ചികമാസത്തിലെ വിശാഖം നക്ഷത്രത്തില്‍ ജനിച്ച എന്റെ 2008-ലെ നാല്‍പ്പത്തിമൂന്നാം പിറന്നാള്‍ എന്നാണെന്നു നോക്കാം.

2008 നവംബര്‍ 22 വരെ കടന്നു പോയ ദിവസങ്ങള്‍ ആദ്യം കണ്ടുപിടിക്കാം. 1965 = 4 x 491 + 1, j = 1.

ഇത്രയും ദിവസത്തിനിടയില്‍ കടന്നുപോയ നാളുകള്‍ = 15706 x 0.988225476 = 15521.069 = 15521

27 നാളു കഴിഞ്ഞാല്‍ അതേ നാള്‍ വരുന്നതുകൊണ്ടും 15521 = 574 x 27 + 23 ആയതിനാലും ഇതു് 23 ദിവസത്തിന്റെ വ്യത്യാസമാണു്.

അതായതു് 2008 നവംബര്‍ 22-നു 23 ദിവസം മുമ്പു് വിശാഖമാണു്. അതായതു് ഒക്ടോബര്‍ 30-നു്. അതിനു ശേഷം 27 ദിവസം കഴിഞ്ഞു് (അതായതു് നവംബര്‍ 22-നു 4 ദിവസം കഴിഞ്ഞു്) നവംബര്‍ 26-നും വിശാഖമാണു്.

ഒക്ടോബര്‍ 30, നവംബര്‍ 26 എന്നിവയില്‍ വൃശ്ചികമാസത്തില്‍ വരുന്ന നക്ഷത്രം രണ്ടാമത്തേതായതു കൊണ്ടു് പിറന്നാള്‍ നവംബര്‍ 26-നു്.

ഇത്രയും കണക്കുകൂട്ടലിനെ ഒരു ഗണിതവാക്യമായി താഴെച്ചേര്‍ക്കുന്നു.

ഇത്രയുമാണു് പിറന്നാളിനെ അപേക്ഷിച്ചു ജന്മദിനം മുന്നോട്ടു പോയ ദിവസങ്ങളുടെ എണ്ണം.

അപ്പോള്‍ ജന്മദിനത്തില്‍ നിന്നു d ദിവസം കുറച്ചാല്‍ പിറന്നാള്‍ കിട്ടുമോ? കിട്ടണമെന്നില്ല. ആ ദിവസം ജന്മമാസത്തില്‍ ആവണമെന്നില്ല. എങ്കിലും ഏകദേശം 27 ദിവസത്തില്‍ നക്ഷത്രചക്രം ആവര്‍ത്തിക്കുന്നതു കൊണ്ടു് (BD – d), (BD – d – 27), (BD – d + 27), (BD – d + 54) എന്നിവ ജന്മനക്ഷത്രമായിരിക്കും. അതിലൊന്നു് ഏതായാലും ജന്മമാസമായിരിക്കും. ആ ദിവസം തന്നെ പിറന്നാള്‍.

ചുവന്ന പെന്‍സിലും കൂര്‍പ്പിച്ചു് അങ്ങുമിങ്ങും പലായനം ചെയ്യുന്ന ദേവനെപ്പോലെയുള്ള ഓഡിറ്റര്‍മാര്‍ക്കു് ഫോര്‍മുല ശരിയാവില്ല, പട്ടിക തന്നെ വേണം. ഇതാ പട്ടിക. ഈ പട്ടികയില്‍ -31 മുതല്‍ +31 വരെയുള്ള എല്ലാ (രണ്ടെണ്ണമോ മൂന്നെണ്ണമോ) മൂല്യങ്ങളും കൊടുത്തിട്ടുണ്ടു്. ഇവയിലൊന്നു പിറന്നാളായിരിക്കും. പൂജ്യത്തിനോടു വളരെ അടുത്തുള്ളവയെ കട്ടിയുള്ള അക്ഷരത്തില്‍ കാണിച്ചിട്ടുണ്ടു്.

n j = 0 j = 1 j = 2 j = 3 1 -10 , 17 -10 , 17 -10 , 17 -11 , 16 2 -19 , 8 -19 , 8 -20 , 7 -20 , 7 3 -29 , -2 , 25 -30 , -3 , 24 -30 , -3 , 24 -30 , -3 , 24 4 -13 , 14 -13 , 14 -13 , 14 -13 , 14 5 -22 , 5 -22 , 5 -22 , 5 -23 , 4 , 31 6 -5 , 22 -5 , 22 -6 , 21 -6 , 21 7 -15 , 12 -16 , 11 -16 , 11 -16 , 11 8 -26 , 1 , 28 -26 , 1 , 28 -26 , 1 , 28 -26 , 1 , 28 9 -8 , 19 -8 , 19 -8 , 19 -9 , 18 10 -18 , 9 -18 , 9 -19 , 8 -19 , 8 11 -28 , -1 , 26 -29 , -2 , 25 -29 , -2 , 25 -29 , -2 , 25 12 -11 , 16 -11 , 16 -11 , 16 -11 , 16 13 -21 , 6 -21 , 6 -21 , 6 -22 , 5 14 -31 , -4 , 23 -31 , -4 , 23 -5 , 22 -5 , 22 15 -13 , 14 -14 , 13 -14 , 13 -14 , 13 16 -24 , 3 , 30 -24 , 3 , 30 -24 , 3 , 30 -24 , 3 , 30 17 -7 , 20 -7 , 20 -7 , 20 -8 , 19 18 -17 , 10 -17 , 10 -18 , 9 -18 , 9 19 -26 , 1 , 28 -27 , 0 , 27 -27 , 0 , 27 -27 , 0 , 27 20 -10 , 17 -10 , 17 -10 , 17 -10 , 17 21 -20 , 7 -20 , 7 -20 , 7 -21 , 6 22 -29 , -2 , 25 -29 , -2 , 25 -30 , -3 , 24 -30 , -3 , 24 23 -12 , 15 -13 , 14 -13 , 14 -13 , 14 24 -23 , 4 , 31 -23 , 4 , 31 -23 , 4 , 31 -23 , 4 , 31 25 -5 , 22 -5 , 22 -5 , 22 -6 , 21 26 -15 , 12 -15 , 12 -16 , 11 -16 , 11 27 -25 , 2 , 29 -26 , 1 , 28 -26 , 1 , 28 -26 , 1 , 28 28 -9 , 18 -9 , 18 -9 , 18 -9 , 18 29 -18 , 9 -18 , 9 -18 , 9 -19 , 8 30 -28 , -1 , 26 -28 , -1 , 26 -29 , -2 , 25 -29 , -2 , 25 31 -11 , 16 -12 , 15 -12 , 15 -12 , 15 32 -21 , 6 -21 , 6 -21 , 6 -21 , 6 33 -31 , -4 , 23 -31 , -4 , 23 -31 , -4 , 23 -5 , 22 34 -14 , 13 -14 , 13 -15 , 12 -15 , 12 35 -23 , 4 , 31 -24 , 3 , 30 -24 , 3 , 30 -24 , 3 , 30 36 -7 , 20 -7 , 20 -7 , 20 -7 , 20 37 -17 , 10 -17 , 10 -17 , 10 -18 , 9 38 -27 , 0 , 27 -27 , 0 , 27 -28 , -1 , 26 -28 , -1 , 26 39 -9 , 18 -10 , 17 -10 , 17 -10 , 17 40 -20 , 7 -20 , 7 -20 , 7 -20 , 7 41 -30 , -3 , 24 -30 , -3 , 24 -30 , -3 , 24 -31 , -4 , 23 42 -12 , 15 -12 , 15 -13 , 14 -13 , 14 43 -22 , 5 -23 , 4 , 31 -23 , 4 , 31 -23 , 4 , 31 44 -6 , 21 -6 , 21 -6 , 21 -6 , 21 45 -15 , 12 -15 , 12 -15 , 12 -16 , 11 46 -25 , 2 , 29 -25 , 2 , 29 -26 , 1 , 28 -26 , 1 , 28 47 -8 , 19 -9 , 18 -9 , 18 -9 , 18 48 -19 , 8 -19 , 8 -19 , 8 -19 , 8 49 -28 , -1 , 26 -28 , -1 , 26 -28 , -1 , 26 -29 , -2 , 25 50 -11 , 16 -11 , 16 -12 , 15 -12 , 15		n j = 0 j = 1 j = 2 j = 3 51 -21 , 6 -22 , 5 -22 , 5 -22 , 5 52 -31 , -4 , 23 -31 , -4 , 23 -31 , -4 , 23 -31 , -4 , 23 53 -14 , 13 -14 , 13 -14 , 13 -15 , 12 54 -24 , 3 , 30 -24 , 3 , 30 -25 , 2 , 29 -25 , 2 , 29 55 -6 , 21 -7 , 20 -7 , 20 -7 , 20 56 -17 , 10 -17 , 10 -17 , 10 -17 , 10 57 -27 , 0 , 27 -27 , 0 , 27 -27 , 0 , 27 -28 , -1 , 26 58 -10 , 17 -10 , 17 -11 , 16 -11 , 16 59 -19 , 8 -20 , 7 -20 , 7 -20 , 7 60 -30 , -3 , 24 -30 , -3 , 24 -30 , -3 , 24 -30 , -3 , 24 61 -13 , 14 -13 , 14 -13 , 14 -14 , 13 62 -22 , 5 -22 , 5 -23 , 4 , 31 -23 , 4 , 31 63 -5 , 22 -6 , 21 -6 , 21 -6 , 21 64 -16 , 11 -16 , 11 -16 , 11 -16 , 11 65 -25 , 2 , 29 -25 , 2 , 29 -25 , 2 , 29 -26 , 1 , 28 66 -8 , 19 -8 , 19 -9 , 18 -9 , 18 67 -18 , 9 -19 , 8 -19 , 8 -19 , 8 68 -29 , -2 , 25 -29 , -2 , 25 -29 , -2 , 25 -29 , -2 , 25 69 -11 , 16 -11 , 16 -11 , 16 -12 , 15 70 -21 , 6 -21 , 6 -22 , 5 -22 , 5 71 -31 , -4 , 23 -5 , 22 -5 , 22 -5 , 22 72 -14 , 13 -14 , 13 -14 , 13 -14 , 13 73 -24 , 3 , 30 -24 , 3 , 30 -24 , 3 , 30 -25 , 2 , 29 74 -7 , 20 -7 , 20 -8 , 19 -8 , 19 75 -16 , 11 -17 , 10 -17 , 10 -17 , 10 76 -27 , 0 , 27 -27 , 0 , 27 -27 , 0 , 27 -27 , 0 , 27 77 -10 , 17 -10 , 17 -10 , 17 -11 , 16 78 -20 , 7 -20 , 7 -21 , 6 -21 , 6 79 -29 , -2 , 25 -30 , -3 , 24 -30 , -3 , 24 -30 , -3 , 24 80 -13 , 14 -13 , 14 -13 , 14 -13 , 14 81 -23 , 4 , 31 -23 , 4 , 31 -23 , 4 , 31 -24 , 3 , 30 82 -5 , 22 -5 , 22 -6 , 21 -6 , 21 83 -15 , 12 -16 , 11 -16 , 11 -16 , 11 84 -26 , 1 , 28 -26 , 1 , 28 -26 , 1 , 28 -26 , 1 , 28 85 -8 , 19 -8 , 19 -8 , 19 -9 , 18 86 -18 , 9 -18 , 9 -19 , 8 -19 , 8 87 -28 , -1 , 26 -29 , -2 , 25 -29 , -2 , 25 -29 , -2 , 25 88 -12 , 15 -12 , 15 -12 , 15 -12 , 15 89 -21 , 6 -21 , 6 -21 , 6 -22 , 5 90 -31 , -4 , 23 -31 , -4 , 23 -5 , 22 -5 , 22 91 -14 , 13 -15 , 12 -15 , 12 -15 , 12 92 -24 , 3 , 30 -24 , 3 , 30 -24 , 3 , 30 -24 , 3 , 30 93 -7 , 20 -7 , 20 -7 , 20 -8 , 19 94 -17 , 10 -17 , 10 -18 , 9 -18 , 9 95 -26 , 1 , 28 -27 , 0 , 27 -27 , 0 , 27 -27 , 0 , 27 96 -10 , 17 -10 , 17 -10 , 17 -10 , 17 97 -20 , 7 -20 , 7 -20 , 7 -21 , 6 98 -30 , -3 , 24 -30 , -3 , 24 -31 , -4 , 23 -31 , -4 , 23 99 -12 , 15 -13 , 14 -13 , 14 -13 , 14 100 -23 , 4 , 31 -23 , 4 , 31 -23 , 4 , 31 -23 , 4 , 31

ഇതില്‍ വ്യത്യാസം പൂജ്യത്തിനോടു വളരെ അടുത്തു വരുന്നവ കട്ടിയുള്ള അക്ഷരത്തില്‍ കാണിച്ചിരിക്കുന്നു. ആ വര്‍ഷങ്ങളിലാണു് ജന്മദിനവും പിറന്നാളും ഒന്നിക്കാന്‍ സാദ്ധ്യതയുള്ളതു്. 19-ന്റെ ഗുണിതങ്ങളില്‍ കട്ടിയക്ഷരമാണുള്ളതെന്നതു ശ്രദ്ധിക്കുക.

---

ഇനി, ചില സാമാന്യ ചോദ്യങ്ങള്‍:

1. ഒരിക്കലും (പത്തൊന്‍പതാം പിറന്നാളിനു പോലും) ജന്മദിനവും പിറന്നാളും ഒന്നിച്ചു വരാത്ത ആരെങ്കിലുമുണ്ടോ?

   ഉണ്ടു്. ചില നക്ഷത്രങ്ങള്‍ ഒരു മാസത്തില്‍ രണ്ടെണ്ണം ഉണ്ടാവും. ഒന്നു് മാസത്തിന്റെ ആദിയിലും മറ്റൊന്നു് അവസാനത്തിലും. ഇവയില്‍ ആദ്യത്തെ നാളില്‍ ജനിച്ചവര്‍ക്കു് ഒരിക്കലും ജന്മദിനവും പിറന്നാളും ഒന്നിച്ചു വരില്ല. 19 തുടങ്ങിയ വര്‍ഷങ്ങളില്‍ അവരുടെ ജന്മദിനത്തിനു തന്നെ നാള്‍ വരുന്നുണ്ടു്. എങ്കിലും, ഒരു മാസത്തില്‍ നാള്‍ രണ്ടു തവണ വരുന്നുണ്ടെങ്കില്‍ അവസാനത്തേതാണു പിറന്നാളായി എടുക്കുന്നതു്. അതുകൊണ്ടാണു് ഇതു്.

2. 19, 38 തുടങ്ങിയ ജന്മദിനങ്ങളില്‍ പിറന്നാള്‍ വരാത്തവരുണ്ടോ?

   ഉണ്ടു്. നാളിന്റെയും ദിവസത്തിന്റെയും ഒരറ്റത്തു ജനിച്ചവര്‍. ഉദാഹരണമായി, അര്‍ദ്ധരാത്രി കഴിഞ്ഞു് അഞ്ചു നിമിഷത്തിനകം ഒരു നക്ഷത്രം തീരുകയാണെങ്കില്‍ അതിനിടയില്‍ ജനിക്കുന്ന കുട്ടിയുടെ പത്തൊന്‍പതാം പിറന്നാള്‍ വരുന്നതു് ജന്മദിനത്തിന്റെ തലേന്നായിരിക്കും.

   അതു പോലെ, സൂര്യോദയത്തിനു ശേഷം അല്പം കഴിഞ്ഞു് ഒരു നാള്‍ തുടങ്ങുകയാണെങ്കില്‍ അന്നത്തെ നക്ഷത്രം കലണ്ടറില്‍ തലേതായിരിക്കും. അങ്ങനെയും ഒരു ദിവസത്തിന്റെ വ്യത്യാസമുണ്ടാവാം.

   മുകളില്‍ പറഞ്ഞ രണ്ടു കാര്യവും കൂടി ഒന്നിച്ചു വന്നാല്‍ കലണ്ടറില്‍ കാണുന്നതില്‍ നിന്നു രണ്ടു ദിവസം വരെ വ്യത്യാസമുണ്ടാകാം. ഇതു് ഈ പോസ്റ്റില്‍ പറഞ്ഞിരിക്കുന്ന എല്ലാ കണക്കുകൂട്ടലുകള്‍ക്കും ബാധകമാണു്.

3. 19, 38 തുടങ്ങിയവയല്ലാതെ വേറെ ഏതെങ്കിലും ജന്മദിനങ്ങളില്‍ പിറന്നാള്‍ ഉണ്ടാവാമോ?

   ഉണ്ടാവാം. പട്ടികയില്‍ 0 എന്നു വരുന്ന വര്‍ഷങ്ങളിലാണല്ലോ അവ ഒന്നാകുന്നതു്. നക്ഷത്രങ്ങളും ദിവസങ്ങളും ഒന്നിച്ചു തുടങ്ങുകയും കഴിയുകയും ചെയ്യാത്തതുകൊണ്ടു് -1, 1 എന്നിവ വരുന്ന വര്‍ഷങ്ങളിലും ഇതു സംഭവിച്ചേക്കാം. പട്ടിക നോക്കിയാല്‍ 8, 11, 27, 30, 46, 49, 65, 84, 87 എന്നീ വര്‍ഷങ്ങളില്‍ (ഞാന്‍ അവ കട്ടിയുള്ള അക്കങ്ങളില്‍ കൊടുത്തിട്ടുണ്ടു്) ഒരു ദിവസത്തെ വ്യത്യാസമേ ഉള്ളൂ എന്നു കാണാം. നാളിന്റെയോ ദിവസത്തിന്റെയോ ഒരറ്റത്തു ജനിച്ചവര്‍ക്കു് വ്യത്യാസം പൂജ്യം ദിവസമായേക്കാം.

---

ആകെ ചിന്താക്കുഴപ്പമായെങ്കില്‍ ചില ഉദാഹരണങ്ങള്‍:

1. എന്റെ പേരു് സന്തോഷ്. തുലാമാസത്തിലെ ഭരണി നാളില്‍ ജനിച്ച എന്റെ മകന്‍ അച്ചുവിന്റെ 2007-ലെ പിറന്നാള്‍ ഒക്ടോബര്‍ 27-നായിരുന്നു. 2008-ല്‍ അതു് എന്നാണു്?

   2007 = 501 x 4 + 3 ആയതിനാല്‍ j = 3.

   n = 1, j = 3 എന്നിവയ്ക്കു യോജിച്ച ദിനവ്യത്യാസം പട്ടികയോ ഫോര്‍മുലയോ ഉപയോഗിച്ചു കണ്ടുപിടിച്ചാല്‍ -10, 17 എന്നു കാണാം. അതായതു് ഒക്ടോബര്‍ 7 അല്ലെങ്കില്‍ നവംബര്‍ 13. തുലാമാസമായതിനാല്‍ പിറന്നാള്‍ നവംബര്‍ 13-നു്.

2. ചോദ്യം: എന്റെ പേരു് ദേവന്‍. ഞാന്‍ ആയിരത്തി തൊള്ളായിരത്തി അറുപത്തൊമ്പത് ജൂണ്‍ പതിനാറിനു ജനിച്ചു. മിഥുനത്തിലെ തിരുവാതിര. എന്റെ മുപ്പത്തെട്ടാം പിറന്നാള്‍ ജന്മദിനത്തിനു തന്നെ ആയിരുന്നു എന്നു സങ്കുചിതന്‍ പറയുന്നു. ശരിയാണോ? എന്റെ മുപ്പത്തൊന്‌പതാം പിറന്നാളിനു ബഡ്‌വൈസര്‍ പൊട്ടിച്ചൊഴിച്ച പാലടപ്രഥമന്‍ കഴിച്ചാല്‍ കൊള്ളാമെന്നുണ്ടു്. (ആലുവായ്ക്കു വടക്കല്ലാത്തതിനാല്‍ മൊളകൂഷ്യം വേണ്ട.) ഈ കരിദിനം എന്നാണു്?

   ഉത്തരം: കുട്ടീ, നിര്‍ത്തി നിര്‍ത്തി ഓരോ ചോദ്യമായി ചോദിക്കൂ. 1969 = 4 x 492 + 1 ആയതിനാല്‍ j = 1.

   1. ഗണിതവാക്യമോ പട്ടികയോ ഉപയോഗിച്ചാല്‍ j = 1, n = 38 എന്നതിനു നേരേ -27, 0, 27 എന്നു കാണാം. 2007 ജൂണ്‍ 16 തിരുവാതിര തന്നെ. എങ്കിലും അതിനു ശേഷം 27 ദിവസം കഴിഞ്ഞുള്ള ജൂലൈ 13-ഉം തിരുവാതിര തന്നെ. അതും മിഥുനമാസമായതു കൊണ്ടു് അതാണു പിറന്നാള്‍.

      മുകളില്‍ ഒന്നാമതു പറഞ്ഞിരിക്കുന്ന സ്ഥിതിയാണു ദേവന്റേതു്. അദ്ദേഹത്തിനു് ഒരിക്കലും ജന്മദിനവും പിറന്നാളും ഒരേ ദിവസം വരുകില്ല. മലയാളമാസത്തിലെ ആദ്യത്തെ രണ്ടുമൂന്നു ദിവസങ്ങളില്‍ ജനിക്കുന്നവര്‍ക്കെല്ലാം ഇതാണു സ്ഥിതി.

   2. ഗണിതവാക്യമോ പട്ടികയോ ഉപയോഗിച്ചാല്‍ j = 1, n = 39 എന്നതിനു നേരേ -10, 17 എന്നു കാണാം. 2008 ജൂണ്‍ 16-നു 10 ദിവസം മുമ്പുള്ള ജൂണ്‍ 6, 17 ദിവസം കഴിഞ്ഞുള്ള ജൂലൈ 3 എന്നിവ തിരുവാതിര തന്നെ. ജനനം മിഥുനത്തിലായതിനാല്‍ പിറന്നാള്‍ ജൂലൈ 3-നു്. അമേരിക്കയ്ക്കു വന്നാല്‍ പിറ്റേ ദിവസം വെടിക്കെട്ടും കാണാം.
3. ചോദ്യം: എന്റെ പേരു പെരിങ്ങോടന്‍. 1981 മെയ് 11-നു മേടമാസത്തിലെ മകം നക്ഷത്രത്തില്‍ ജനനം. 2007-ലെ എന്റെ പിറന്നാളിനു ഞാന്‍ “ഖകമേ…” എന്നൊരു വിശിഷ്ടകൃതി രചിക്കുകയുണ്ടായി. (പ്രസിദ്ധീകരിച്ചതു് ഏതാനും ദിവസങ്ങള്‍ക്കു ശേഷമാണു്.) 2057-ലെ എന്റെ പിറന്നാളിനു് ഈ കൃതിയുടെ അന്‍പതാം വാര്‍ഷികം ആഘോഷിക്കാന്‍ എന്റെ ആരാധകര്‍ തീരുമാനിച്ചിരിക്കുന്നു. അതിനുള്ള ഒരുക്കം ഇപ്പോഴേ തുടങ്ങി. ഒരു പ്രശ്നമേയുള്ളൂ. അതു് ഏതു തീയതിയാണു് എന്നറിയിക്കണം. സഹായിക്കാമോ?

   ഉത്തരം: 2057-ല്‍ പെരിങ്ങോടനു് 76 വയസ്സു തികയും. 76 എന്നതു 19-ന്റെ ഗുണിതമായതു കൊണ്ടു മിക്കവാറും പിറന്നാള്‍ മെയ് 11-നു തന്നെ ആയിരിക്കും. എങ്കിലും ഒന്നു കണക്കുകൂട്ടി നോക്കാം.

   1981 = 4 x 495 + 1 ആയതു കൊണ്ടു് j = 1. n = 76, j = 1 എന്നിവയ്ക്കു പട്ടികയില്‍ നിന്നോ ഗണിതവാക്യത്തില്‍ നിന്നോ -27, 0, 27 എന്നു കാണാം.

   അതായതു്, 2057 മെയ് 11-നും 27 ദിവസം കഴിഞ്ഞു ജൂണ്‍ 7-നും മകം ആയിരിക്കും എന്നു്. അതില്‍ മേടമാസത്തില്‍ ഉള്ള മകം മെയ് 11 തന്നെ ആയതുകൊണ്ടു് അന്നാണു പെരിങ്ങോടന്റെ പെരിങ്ങോടന്റെ പിറന്നാളും “ഖകമേ…” സുവര്‍ണ്ണജൂബിലിയും.

   അതു പറയാന്‍ വരട്ടേ. കലണ്ടറില്‍ നോക്കിയാല്‍ 2057 മെയ് 11 മകമല്ല പൂയമാണെന്നു കാണാം. മെയ് 13-നാണു മകം.

   മുകളില്‍ കൊടുത്ത രണ്ടാമത്തെ സ്ഥിതിയാണു് ഇതു്. പെരിങ്ങോടന്‍ ജനിച്ച 1981 മെയ് 11-നു രാവിലെ 10:18 വരെ ആയില്യമായിരുന്നു. അതിനു ശേഷം പിറ്റേന്നു രാവിലെ 11:44 വരെയാണു മകം. പെരിങ്ങോടന്റെ ജനനത്തീയതിയില്‍ സൂര്യോദയത്തിനുള്ള നാള്‍ (ഇതു തന്നെയാണു സാധാരണ കലണ്ടറിലും കാണുക) ആയില്യമാണു്.

   ഇനി 2057-ല്‍ മെയ് 12-നു രാവിലെ 8:23-നു മകം തുടങ്ങും. സൂര്യോദയത്തിനു മകം തുടങ്ങാഞ്ഞതു കൊണ്ടു പിറ്റേന്നേ മകമായി കണക്കാക്കൂ എന്നു മാത്രം.

   ഈ രണ്ടു വ്യത്യാസങ്ങളും കൂടി ഒന്നിച്ചു ചേര്‍ന്നപ്പോള്‍ രണ്ടു ദിവസത്തെ വ്യത്യാസമുണ്ടായി എന്നു മാത്രം.

4. ചോദ്യം: ഞാന്‍ ശനിയന്‍. ഇവന്‍ ശ്രീജിത്ത്. ഞങ്ങള്‍ രണ്ടുപേരും 1979-ലാണു ജനിച്ചതു്. ഞാന്‍ ജനുവരി 14-നു്. (രാവിലെ ജനിച്ചതു കൊണ്ടു് ധനുമാസത്തിലെ പൂയം.) ഇവന്‍ ജൂലൈ 15-നു് (ഉച്ചയ്ക്കു ശേഷം ജനിച്ചതു കൊണ്ടു് മിഥുനമാസത്തിലെ രേവതി.). ഞങ്ങള്‍ ഞങ്ങളുടെ ഷഷ്ടിപൂര്‍ത്തി വിപുലമായി 2039-ല്‍ ആഘോഷിക്കാന്‍ തീരുമാനിച്ചു. ഏതൊക്കെ തീയതിയിലാണു് അവ എന്നു പറയാമോ?

   ഉത്തരം: ശനിയന്‍ ജനുവരിയില്‍ ജനിച്ചതു കൊണ്ടു മുന്‍‌പുള്ള വര്‍ഷം നോക്കണം. 1978 = 4 x 494 + 2, j = 2. ശ്രീജിത്ത് ജൂണിലായതിനാല്‍ j = 3.

   n = 60, എന്നതിനു പട്ടിക ഉപയോഗിച്ചാല്‍ j എത്രയായാലും -30, -3, 24 എന്നു കാണാം. അതായതു് മൂന്നു ദിവസം മുമ്പും 24 ദിവസത്തിനു ശേഷവും. 2039-ല്‍ അതേ മാസത്തില്‍ വരാന്‍ രണ്ടു പേര്‍ക്കും ജന്മദിനത്തിന്റെ മൂന്നു ദിവസം മുമ്പായിരിക്കും ഷഷ്ടിപൂര്‍ത്തി. ശനിയനു ജനുവരി 11-നു്; ശ്രീജിത്തിനു ജൂലൈ 12-നു്.

   പിന്നെ, കാര്യമൊക്കെ കൊള്ളാം, ശ്രീജിത്തിന്റെ കൂടെ എന്തെങ്കിലും ചെയ്തിട്ടുണ്ടെങ്കില്‍ അതു കുളമായിട്ടേ ഉള്ളൂ എന്നു മറക്കേണ്ട!

---

ചുരുക്കത്തില്‍,

1. സാധാരണയായി, 19-ന്റെ ഗുണിതങ്ങളായുള്ള ജന്മദിനങ്ങളില്‍ത്തന്നെ പിറന്നാളും വരും.
2. 19-ന്റെ ഗുണിതമല്ലാത്ത ചില ജന്മദിനങ്ങളിലും ഇതു സംഭവിച്ചേക്കാം. എണ്ണത്തില്‍ കുറവാണെന്നു മാത്രം.
3. 19-ന്റെ ഗുണിതത്തിലും ചിലര്‍ക്കു് ഉണ്ടാകണമെന്നില്ല. അതിന്റെ തലേന്നോ പിറ്റേന്നോ ആവാം.
4. ചില ആളുകള്‍ക്കു് ഒരിക്കലും ഇവ രണ്ടും ഒരിക്കലും ഒന്നിച്ചു വരില്ല. ആ മാസത്തിലെ പിന്നീടുള്ള നാളിനാവും പിറന്നാള്‍.
5. മിക്കവാറും എല്ലാ ആളുകള്‍ക്കും ഈ പോസ്റ്റില്‍ കൊടുത്തിരിക്കുന്ന സൂത്രവാക്യമോ പട്ടികയോ ഉപയോഗിച്ചു് ഓരോ വര്‍ഷവും ജന്മദിനവും പിറന്നാളും തമ്മിലുള്ള വ്യത്യാസം എത്ര ദിവസമാണെന്നു കണ്ടുപിടിക്കാം. ഇതു തന്നെ നക്ഷത്രങ്ങളെ അടിസ്ഥാനപ്പെടുത്തിയിട്ടുള്ള വിശേഷദിവസങ്ങള്‍ക്കും ഉപയോഗിക്കാം.

---

ഈ പോസ്റ്റ് ഇന്നലെ (ജനുവരി 14) ജന്മദിനം ആഘോഷിച്ച ശനിയനു സമര്‍പ്പിക്കുന്നു. ഇന്നലെ പോസ്റ്റു ചെയ്യണമെന്നു കരുതിയതാണു്. പറ്റിയില്ല.

---

എല്ലാവരോടും ഒരു അഭ്യര്‍ത്ഥന:

നിങ്ങള്‍ക്കറിയാവുന്ന തീയതികളും നക്ഷത്രങ്ങളും ഉപയോഗിച്ചു് ഈ പോസ്റ്റില്‍ പറഞ്ഞിരിക്കുന്ന കാര്യങ്ങള്‍ ശരിയാണോ എന്നു ദയവായി ടെസ്റ്റു ചെയ്യുക. രണ്ടു ദിവസത്തില്‍ കൂടുതല്‍ വ്യത്യാസമുണ്ടെങ്കില്‍ ദയവായി ഒരു കമന്റു വഴിയോ ഈമെയില്‍ വഴിയോ എന്നെ അറിയിക്കുക.

മുന്‍‌കൂറായി എല്ലാവര്‍ക്കും നന്ദി.

ഒരു പഴയ രസികന്‍ സംസ്കൃതശ്ലോകം.

കവിതാരസചാതുര്യം
വ്യാഖ്യാതാ വേത്തി നോ കവിഃ
സുതാസുരതസാമര്‍ത്ഥ്യം
ജാമാതാ വേത്തി നോ പിതാ

അര്‍ത്ഥം:

കവിതാ-രസ-ചാതുര്യം	:	കവിതയുടെ രസത്തിനുള്ള മഹത്ത്വം
വ്യാഖ്യാതാ വേത്തി	:	വ്യാഖ്യാതാവിനറിയാം
നോ കവിഃ	:	കവിയ്ക്കറിയില്ല
സുതാ-സുരത-സാമര്‍ത്ഥ്യം	:	മകള്‍ക്കു രതിക്രീഡയിലുള്ള സാമര്‍ത്ഥ്യം
ജാമാതാ വേത്തി	:	മരുമകനേ അറിയൂ
നോ പിതാ	:	പിതാവിനറിയില്ല.

കൂടുതല്‍ വിശദീകരണം ആവശ്യമില്ലെന്നു തോന്നുന്നു.

ഇതുപോലെ ഒരു തത്ത്വവും അതിനൊരു രസികന്‍ ഉദാഹരണവും കൊടുക്കുന്ന സംസ്കൃതശ്ലോകങ്ങള്‍ ധാരാളമുണ്ടു്. അര്‍ത്ഥാന്തരന്യാസം, ദൃഷ്ടാന്തം എന്ന അലങ്കാരങ്ങളുടെ ചമല്‍ക്കാരവും ഇത്തരം താരതമ്യമാണു്.

അച്ഛന്‍ പൊന്നുപോലെ നോക്കിയ മകളെ ജാമാതാക്കള്‍ കൊണ്ടു പോയി പിഴപ്പിച്ച കഥകളും ധാരാളമുണ്ടു്. കവിതയുടെയും വ്യാഖ്യാതാക്കളുടെയും കാര്യത്തില്‍ അവ അല്പം കൂടുതലുമാണു്. അതൊരു വലിയ പോസ്റ്റിനുള്ള വിഷയമായതിനാല്‍ തത്ക്കാലം അതിനു തുനിയുന്നില്ല.

സന്തോഷ് തോട്ടിങ്ങലിന്റെ ഈ പോസ്റ്റിന്റെ ചര്‍ച്ചയ്ക്കിടയില്‍ വാല്മീകി ഇട്ട ഈ കമന്റാണു് ഇപ്പോള്‍ ഇതു പോസ്റ്റു ചെയ്യാന്‍ പ്രചോദനം.

---

ഇതിന്റെ പരിഭാഷകള്‍ ഒന്നുമറിയില്ല. ഇതിനെ അവലംബിച്ചു വരമൊഴിയെപ്പറ്റി ഞാന്‍ ഒരിക്കല്‍ എഴുതിയ ശ്ലോകം താഴെ:

വരമൊഴിയുടെ മേന്മ നമ്മളെല്ലാ-
വരുമറിയും, സിബുവെന്തറിഞ്ഞു പാവം!
മരുമകനറിയും മകള്‍ക്കു വായ്ക്കും
സുരതപടുത്വ, മതച്ഛനെന്തറിഞ്ഞു?

ഇതു് എല്ലാ കണ്ടുപിടിത്തങ്ങള്‍ക്കും ബാധകമാണു്. ടെലഫോണിനെപ്പറ്റി ഗ്രഹാം ബെല്ലിനെക്കാളും ഇലക്ട്രിക് ബള്‍ബിനെപ്പറ്റി എഡിസനെക്കാളും പില്‍ക്കാലത്തുള്ളവര്‍ മനസ്സിലാക്കി. സ്റ്റാള്‍മാനെക്കാള്‍ ഇമാക്സും സന്തോഷ് തോട്ടിങ്ങലിനെക്കാള്‍ മലയാളം സ്പെല്‍ ചെക്കറും ഉപയോഗിക്കുന്നതും അതിന്റെ ഗുണങ്ങള്‍ മനസ്സിലാക്കുന്നതും അതിന്റെ ഉപയോക്താക്കളാണു്.

കലണ്ടറുകളെപ്പറ്റി പ്രതിപാദിച്ച കഴിഞ്ഞ പോസ്റ്റിനു ശേഷവും അലപ്ര(FAQ)കള്‍ക്കു കുറവുണ്ടായില്ല. അവയില്‍ പ്രധാനമായതു് നക്ഷത്രം, തിഥി തുടങ്ങിയവ എന്റെ കലണ്ടറില്‍ കണ്ടുപിടിക്കാന്‍ ബുദ്ധിമുട്ടാണു് എന്നതായിരുന്നു. ഈ ചോദ്യങ്ങളില്‍ക്കൂടി പോയപ്പോള്‍ സാധാരണ കലണ്ടറുകളില്‍ കൊടുത്തിരിക്കുന്ന വിവരങ്ങളും കാര്യമായി ആളുകള്‍ക്കു മനസ്സിലാകുന്നില്ല എന്നു മനസ്സിലായി. കലണ്ടറുകളിലെ ചില വിവരങ്ങള്‍ മനസ്സിലാക്കാന്‍ ഒരു ശ്രമമാണു് ഈ പോസ്റ്റില്‍.

ഇതില്‍ കൊടുത്തിട്ടുള്ള ചിത്രങ്ങള്‍ വലിപ്പം കുറച്ചതുകൊണ്ടു ചിലപ്പോള്‍ വ്യക്തത കുറഞ്ഞതായേക്കാം. അതില്‍ ക്ലിക്കു ചെയ്താല്‍ വലിയ ചിത്രം കിട്ടും.

ഉദാഹരണം കാണിക്കാന്‍ 2008-ലെ ഓണ്‍‌ലൈന്‍ കലണ്ടറൊന്നും കിട്ടിയില്ല. അതിനാല്‍ 2007 ഡിസംബറിലെ ദീപിക കലണ്ടര്‍ ഇവിടെ നിന്നും എടുത്തു. താരതമ്യത്തിനായി 2007-ലെ എന്റെ ആലുവാ കലണ്ടര്‍ ഇവിടെ നിന്നും.

സൌകര്യത്തിനു വേണ്ടി, ഈ പോസ്റ്റില്‍ സാധാരണ നാം അച്ചടിയിലോ ഓണ്‍‌ലൈനായോ കാണുന്ന കലണ്ടറുകളെ ഒന്നിച്ചു് “ദീപിക കലണ്ടര്‍” എന്നു വിളിക്കുന്നു. ഇവ ഏതു കലണ്ടറിലും നോക്കാം. ഞാന്‍ പ്രസിദ്ധീകരിച്ച PDF കലണ്ടറിനെ “എന്റെ കലണ്ടര്‍” എന്നും.

---

ആദ്യമായി തീയതികള്‍. ഇതില്‍ സംശയമൊന്നും ഉണ്ടാവാന്‍ സാദ്ധ്യതയില്ല.

കലണ്ടറില്‍ ഇംഗ്ലീഷ് (ഗ്രിഗോറിയന്‍), മലയാളം (കൊല്ലവര്‍ഷം), ശകവര്‍ഷം എന്നിവയിലെ തീയതികള്‍ ഉണ്ടാവും. ഇവ എന്റെ കലണ്ടറില്‍ ആദ്യത്തെ മൂന്നു കോളത്തില്‍ ഉണ്ടു്. (നാട്ടിലെ കലണ്ടറില്‍ ഉള്ള ഹിജ്‌റ വര്‍ഷത്തീയതികള്‍ എന്റെ കലണ്ടറില്‍ ഇല്ല.) കലണ്ടറില്‍ മുകളില്‍ (അല്ലെങ്കില്‍ ഇടത്തു്) ഉള്ള ആഴ്ച എന്റെ കലണ്ടറില്‍ അടുത്ത കോളത്തില്‍ ഉണ്ടു്. ഇവയെ താഴെ രേഖപ്പെടുത്തി കാണിച്ചിരിക്കുന്നു.

---

ഇനി നക്ഷത്രം കണ്ടുപിടിക്കുന്നതു്.

ദീപിക കലണ്ടറില്‍ ഡിസംബര്‍ 5-ന്റെ താഴെ ഇങ്ങനെ കാണാം.

ചിത്തിര 47/00

ഇതിന്റെ അര്‍ത്ഥം 5-നു സൂര്യോദയത്തിനു ചിത്തിര നക്ഷത്രമാണെന്നും അതു് അതിനു ശേഷം 47 നാഴികയും 0 വിനാഴികയും കഴിഞ്ഞാല്‍ ചിത്തിര കഴിഞ്ഞു ചോതി ആകും എന്നുമാണു്. 47 നാഴിക = 47 x 24 = 1128 മിനിട്ടു് = 18 മണിക്കൂര്‍ 48 മിനിട്ടു്. എല്ലാ ദിവസത്തിന്റെയും സൂര്യോദയം ദീപിക കലണ്ടറിലില്ല. എന്റെ കലണ്ടറില്‍ അതു 6:31 AM എന്നു കാണാം. അതുകൊണ്ടു് 6:31 + 18:48 = 25:19 അതായതു പിറ്റേ ദിവസം 1:19 AM വരെ ചിത്തിരയാണു്. ദീപിക കലണ്ടര്‍ ഉണ്ടാക്കിയതു് ആലുവയിലെ സമയത്തിനു് ആവില്ല. അതിനാല്‍ ഈ സമയം അല്പം വ്യത്യാസമുണ്ടാവും.

എന്റെ കലണ്ടറില്‍ നോക്കുക. ചിത്തിര മാത്രമേ ഉള്ളൂ. അതിന്റെ അര്‍ത്ഥം 5-നു മുമ്പുള്ള അര്‍ദ്ധരാത്രി മുതല്‍ കഴിഞ്ഞുള്ള അര്‍ദ്ധരാത്രി വരെ ചിത്തിര ആണെന്നാണു്. പിറ്റേ ദിവസം നോക്കിയാല്‍ 1:25 AM വരെ ചിത്തിരയും അതു കഴിഞ്ഞാല്‍ ചോതിയുമാണെന്നു കാണാം.

ഇനി, പിറന്നാള്‍, ഓണം തുടങ്ങിയവ കണക്കാക്കുന്നതു് സൂര്യോദയത്തിനുള്ള നക്ഷത്രം നോക്കിയാണു്. അതുകൊണ്ടു് 5-നു ചിത്തിരയും 6-നു ചോതിയുമാണു്. എന്റെ കലണ്ടറില്‍ സൂര്യോദയത്തിനുള്ള നാളും തിഥിയും കട്ടിയുള്ള അക്ഷരത്തില്‍ കൊടുത്തിരിക്കുന്നു. അവയും അങ്ങനെ തന്നെ എന്നു കാണാം. 6 ചിത്തിരയില്‍ തുടങ്ങുന്നെങ്കിലും ഉദയത്തിനു മുമ്പേ ചോതി ആകുന്നു എന്നു ശ്രദ്ധിക്കുക.

---

ഒരുദാഹരണം കൂടി. ഡിസംബര്‍ 4 നോക്കുക.

ദീപിക കലണ്ടറില്‍ അത്തം 39:28 എന്നാണു്. 24 x (39:28) = 947 മിനിട്ടു് = 15 മണിക്കൂര്‍ 47 മിനിട്ടു്. ഉദയം 6:31-നു് എന്നു കരുതിയാല്‍ അത്തം 22:18 വരെ അതായതു് 10:18 PM വരെ ഉണ്ടെന്നു കാണാം. 10:23 ആണു് എന്റെ കലണ്ടറിലെ സമയം.

തിഥിയും ഇങ്ങനെ തന്നെ കാണാം.

---

ഒരു നക്ഷത്രത്തിന്റെ ദൈര്‍ഘ്യം ഏകദേശം ഒരു ദിവസത്തിന്റെ ദൈര്‍ഘ്യം തന്നെ വരും. അതിനാല്‍ മിക്കവാറും ദിവസങ്ങളില്‍ ഒരു തവണയേ നക്ഷത്രം മാറുകയുള്ളൂ. ഇങ്ങനെയല്ലാതെയും സംഭവിക്കാം. ഒരു ദിവസം നക്ഷത്രം മാറാതെ ഒരേ ദിവസമായിത്തന്നെ നില്‍ക്കുന്നതു് മുകളില്‍ കണ്ടല്ലോ. (ദീപിക കലണ്ടറില്‍ ഇതു് അടുത്തടുത്തു രണ്ടു ദിവസം ഒരേ നക്ഷത്രമായി കാണാം.)

സൂര്യോദയം മുതല്‍ സൂര്യോദയം വരെയുള്ള ദിവസത്തില്‍ രണ്ടു തവണ നക്ഷത്രം മാറിയാല്‍ ദീപിക കലണ്ടറില്‍ അതു രണ്ടും കൊടുത്തിട്ടുണ്ടാവും. ഉദാഹരണം താഴെ (2007 ഡിസംബര്‍ 23).

ഇതനുസരിച്ചു് സൂര്യോദയത്തിനു രോഹിണിനക്ഷത്രം. 1 നാഴിക 52 വിനാഴിക (അതായതു് 48 മിനിട്ടു്) കഴിഞ്ഞാല്‍ മകയിരം. 55 നാഴിക 27 വിനാഴിക (22 മണിക്കൂര്‍ 11 മിനിട്ടു്) കഴിഞ്ഞാല്‍ തിരുവാതിര.

സൂര്യോദയം രാവിലെ 6:40 എന്നു കരുതിയാല്‍ മകയിരം 7:28-നു തുടങ്ങും. തിരുവാതിര അന്നു രാത്രി (പിറ്റേന്നു വെളുപ്പിനു്) 4:51-നും. സൂര്യോദയത്തിനു മുമ്പായതിനാലാണു് അതേ ദിവസം തന്നെ കാണിക്കുന്നതു്.

എന്റെ കലണ്ടറില്‍ ഇവ യഥാക്രമം രാവിലെ 7:28, പിറ്റേന്നു രാവിലെ 4:54 എന്നു കാണാം. എന്റെ കലണ്ടര്‍ അര്‍ദ്ധരാത്രി മുതല്‍ അര്‍ദ്ധരാത്രി വരെയായതു കൊണ്ടു് ഇവ രണ്ടു ദിവസമായാണു കാണിക്കുന്നതു്.

ഇനി, എന്റെ കലണ്ടറിലെ ഒരു ദിവസത്തില്‍ നക്ഷത്രം രണ്ടു പ്രാവശ്യം മാറുന്നതിനു് ഉദാഹരണം. 2007 ഡിസംബര്‍ 26.

എന്റെ കലണ്ടറില്‍, ഡിസംബര്‍ 26 അര്‍ദ്ധരാത്രിയ്ക്കു തൊട്ടു ശേഷം 12:49-നു നക്ഷത്രം പുണര്‍തത്തില്‍ നിന്നു പൂയമാകുന്നു. അന്നു രാത്രി 11:39-നു് പൂയത്തില്‍ നിന്നു് ആയില്യവും.

ദീപിക കലണ്ടറില്‍ ഇതില്‍ ആദ്യത്തേതു് 25-നാണു കാണുക. പുണര്‍തത്തില്‍ നിന്നു പൂയമാകുന്നതു് ഉദയത്തിനു ശേഷം 45 നാഴികയും 20 വിനാഴികയും (അതായതു്, 18 മണിക്കൂര്‍ 8 മിനിറ്റ്) കഴിഞ്ഞാണു്. ഉദയം രാവിലെ 6:41 എന്നു കരുതിയാല്‍ ഇതു സംഭവിക്കുന്നതു് രാത്രി 12:49-നു്.

രണ്ടാമത്തേതു 26-നു തന്നെ. ഉദയാല്‍പ്പരം 42 നാഴികയും 29 വിനാഴികയും (17 മണിക്കൂര്‍) കഴിഞ്ഞു്. ഉദയം 6:42 എന്നു കരുതിയാല്‍ രാത്രി 11:42-നു്.

ദിവസത്തിന്റെ നിര്‍വ്വചനം രണ്ടു കലണ്ടറിലും രണ്ടു വിധമായതുകൊണ്ടു് ഇതു സംഭവിക്കുന്നതു് അവയില്‍ ഒരേ ദിവസമല്ല എന്നും വ്യക്തമായല്ലോ.

പറഞ്ഞുവന്നതു്, എപ്പോള്‍ ഒരു നക്ഷത്രം തീര്‍ന്നിട്ടു് അടുത്തതു തുടങ്ങുന്നു എന്നു കണ്ടുപിടിക്കാന്‍ സാധാരണ കലണ്ടറുകളില്‍ എത്ര ബുദ്ധിമുട്ടാണെന്നു നോക്കുക.

---

ഇനി ഗ്രഹസ്ഫുടങ്ങളുടെ കാര്യം. ദീപിക കലണ്ടറില്‍ ഇതു് ഓരോ മാസത്തിന്റെയും ഒന്നാം തീയതി രാവിലെ 5:30-നുള്ള ഗ്രഹസ്ഥിതി (ഈ രാവിലെ അഞ്ചരയ്ക്കു് എന്താണിത്ര പ്രത്യേകത എന്നു് ആര്‍ക്കെങ്കിലും സംശയമുണ്ടെങ്കില്‍ ജ്യോതിഷവും ശാസ്ത്രവും: ജ്യോത്സ്യന്മാര്‍ ചെയ്യുന്നതെന്തു്? എന്ന പോസ്റ്റ് വായിക്കുക. വിജ്ഞാനം വര്‍ദ്ധിപ്പിക്കുക.) പടം വരച്ചു കാണിക്കുന്നു. മുകളില്‍ ഇടത്തേ അറ്റത്തു മീനം തുടങ്ങി ക്രമത്തില്‍ മേടം, ഇടവം തുടങ്ങി ഓരോ കളവും ഓരോ രാശിയെ സൂചിപ്പിക്കുന്നു. അതിലുള്ള ഗ്രഹങ്ങളുടെ ചുരുക്കരൂപവും കൊടുത്തിരിക്കുന്നു.

ഈ ചിത്രം പട്ടികയായി എഴുതിയാല്‍ ഇങ്ങനെ വരും.

ഗ്രഹം	രാശി
കു (കുജന്‍ – ചൊവ്വ)	മിഥുനം
ച (ചന്ദ്രന്‍)	ചിങ്ങം
മ (മന്ദന്‍ – ശനി)	ചിങ്ങം
ശി (ശിഖി – കേതു)	ചിങ്ങം
ശു (ശുക്രന്‍)	തുലാം
ര (രവി – സൂര്യന്‍)	വൃശ്ചികം
ബു (ബുധന്‍)	വൃശ്ചികം
ഗു (ഗുരു – വ്യാഴം)	ധനു
സ (സര്‍പ്പം – രാഹു)	കുംഭം

എന്റെ കലണ്ടറിലും ഇതു തന്നെ കാണാം. രാശി മാത്രമല്ല, ഗ്രഹസ്ഫുടവും ഉണ്ടു്. എന്റെ മൂല്യങ്ങള്‍ അഞ്ചരയ്ക്കല്ല, അര്‍ദ്ധരാത്രിയ്ക്കാണു് എന്നും ഓര്‍ക്കുക. പക്ഷേ, ഈ ഗ്രഹങ്ങളൊന്നും അഞ്ചര മണിക്കൂറിനുള്ളില്‍ രാശി മാറിയിട്ടില്ല.

---

ഇതു വരെ പറഞ്ഞതു സംഗ്രഹിച്ചാല്‍:

1. ദീപിക കലണ്ടറില്‍ ഒരു തീയതിയ്ക്കു താഴെ ഒരു നക്ഷത്രമോ തിഥിയോ കണ്ടാല്‍ അതിനര്‍ത്ഥം ആ ദിവസം മുഴുവന്‍ ആ നക്ഷത്രം/തിഥി ആണെന്നല്ല. സൂര്യോദയത്തിനു് ആ നക്ഷത്രം/തിഥി ആണെന്നു മാത്രമാണു്. അതിനു വലത്തുവശത്തു കൊടുത്തിരിക്കുന്ന നാഴികവിനാഴികകളാണു് സൂര്യോദയത്തിനു ശേഷം അതിന്റെ ദൈര്‍ഘ്യം. അതിനു ശേഷം അതിനടുത്ത നക്ഷത്രം/തിഥി ആണു്. (സ്വന്തം നക്ഷത്രത്തിനു തന്നെ ക്ഷേത്രദര്‍ശനം നടത്തണമെന്നു നിര്‍ബന്ധമുള്ളവര്‍ വൈകിട്ടാണു് അതു ചെയ്യുന്നതെങ്കില്‍ ഇതു ശ്രദ്ധിക്കുന്നതു നന്നു്.). എന്റെ കലണ്ടറില്‍ ഇതിനു പകരമായി നക്ഷത്രം/തിഥി കട്ടിയുള്ള അക്ഷരത്തില്‍ കൊടുത്തിരിക്കുന്നു. പിറന്നാളിനും വിശേഷദിവസങ്ങള്‍ക്കും മറ്റും അതുപയോഗിക്കാം.
2. ദീപിക കലണ്ടറില്‍ സൂര്യോദയം മുതലാണു് ഒരു ദിവസം തുടങ്ങുന്നതു്. സൂര്യോദയത്തിനു മുമ്പുള്ള സമയം തലേ ദിവസത്തിന്റെ ഭാഗമായാണു കരുതുക. ഭാരതീയപഞ്ചാംഗങ്ങള്‍ പൊതുവേ ഇങ്ങനെയാണു്. സമയങ്ങള്‍ സൂര്യോദയം തൊട്ടുള്ള നാഴികവിനാഴികകളായി രേഖപ്പെടുത്തിയിട്ടുണ്ടാവും.

   എന്റെ കലണ്ടറില്‍ സൌകര്യത്തിനു വേണ്ടി അര്‍ദ്ധരാത്രി മുതല്‍ അര്‍ദ്ധരാത്രി വരെയാണു് ഒരു ദിവസം. ഭാരതീയഗണനത്തിലെ മൂല്യങ്ങള്‍ എളുപ്പത്തില്‍ കിട്ടാന്‍ ചില കാര്യങ്ങള്‍ (നക്ഷത്രം, തിഥി, ലഗ്നം) കട്ടിയുള്ള അക്ഷരത്തില്‍ കൊടുത്തിരിക്കുന്നു.

---

ദീപിക കലണ്ടറും എന്റെ കലണ്ടറും തരുന്ന സമയങ്ങള്‍ ഏകദേശം ഒന്നു തന്നെയാണെങ്കിലും രണ്ടുമൂന്നു മിനിട്ടിന്റെ വ്യത്യാസം പലയിടത്തും കാണാം. താഴെപ്പറയുന്നതില്‍ ഒന്നാവാം കാരണം.

1. ദീപിക കലണ്ടറിനു് അവലംബിച്ച സ്ഥലവും ആലുവായും തമ്മില്‍ സൂര്യോദയത്തിനു് ഏകദേശം 5/6 മിനിട്ടിന്റെ വ്യത്യാസമുണ്ടെന്നു കാ‍ണാം. പക്ഷേ ഇതു മാത്രമല്ല കാരണം. ദീപിക കലണ്ടറിലെ സൂര്യോദയസമയം വെച്ചു നോക്കിയാലും രണ്ടുമൂന്നു മിനിറ്റു വ്യത്യാസം ചിലപ്പോള്‍ കാണുന്നുണ്ടു്.
2. ദീപിക കലണ്ടറിലെ സമയങ്ങള്‍ കണക്കാക്കാന്‍ ഏകദേശക്കണക്കുകളും റൌണ്ടിംഗും മറ്റും ഉപയോഗിക്കുന്നുണ്ടാവും. ഞാന്‍ കഴിയുന്നത്ര കൃത്യത (C++ double type) അവസാനത്തെ കണക്കുകൂട്ടലില്‍ വരെ സൂക്ഷിക്കുന്നുണ്ടു്.
3. അയനാംശത്തില്‍ വ്യത്യാസമുണ്ടാവാം. ലാഹിരി അയനാംശത്തിന്റെ പട്ടികയില്‍ നിന്നു least-square fitting ഉപയോഗിച്ചുണ്ടാക്കിയ ഒരു സൂത്രവാക്യമാണു ഞാന്‍ ഉപയോഗിക്കുന്നതു്.
4. സീയെസ് ഇവിടെ പറയുന്നതു പോലെ എന്റെ പ്രോഗ്രാമില്‍ ഏതോ ബഗ്ഗുണ്ടാവാം.

ഏതായാലും ഇതു കണ്ടുപിടിക്കാന്‍ പല കലണ്ടറുകള്‍ താരതമ്യം ചെയ്തു നോക്കണം. ആരെങ്കിലും സഹായിക്കാനുണ്ടോ? 🙂

---

ഇത്രയും വായിക്കാന്‍ ക്ഷമയുണ്ടായവരോടു്:

കാര്യങ്ങള്‍ വ്യക്തമായെന്നു കരുതുന്നു. ഇല്ലെങ്കില്‍ ഒരു കമന്റിടുക. കൂടുതല്‍ വ്യക്തമാക്കാന്‍ ശ്രമിക്കാം.

കഴിഞ്ഞ കൊല്ലം ചെയ്ത പോലെ ഈക്കൊല്ലവും പഞ്ചാംഗം പ്രസിദ്ധീകരിക്കുന്നു. കഴിഞ്ഞ കൊല്ലം വായനക്കാരുടെ അപേക്ഷപ്രകാരം വിവിധ സ്ഥലങ്ങള്‍ക്കു വേണ്ടി പഞ്ചാംഗം ഉണ്ടാക്കിയിരുന്നു. ആ സ്ഥലങ്ങള്‍ക്കെല്ലാം ഈക്കൊല്ലവും പഞ്ചാംഗങ്ങള്‍ ഉണ്ടാക്കിയിട്ടുണ്ടു്. കൂടുതല്‍ സ്ഥലങ്ങള്‍ക്കു വേണമെങ്കില്‍ ഈ പോസ്റ്റിനൊരു കമന്റിടുകയോ എനിക്കൊരു ഈ-മെയില്‍ അയയ്ക്കുകയോ ചെയ്യുക.

പഞ്ചാംഗം ഈ ബ്ലോഗിന്റെ സൈഡ്‌ബാറില്‍ മലയാളം കലണ്ടര്‍/പഞ്ചാംഗം എന്ന ലിങ്കില്‍ നിന്നു PDF ഫോര്‍മാറ്റില്‍ ഡൌണ്‍‌ലോഡ് ചെയ്യാം. ഇതിനുപയോഗിച്ച തിയറി അവിടെത്തന്നെയുള്ള ഈ പുസ്തകത്തില്‍ വിശദീകരിച്ചിട്ടുണ്ടു്.

---

അടിയ്ക്കടി ലഭിക്കുന്ന പ്രശ്നങ്ങള്‍ (അലപ്ര) [Frequently Asked Questions]

കഴിഞ്ഞ കൊല്ലം ഈ പഞ്ചാംഗം പ്രസിദ്ധീകരിച്ചപ്പോള്‍ വായനക്കാര്‍ ചോദിച്ചതും ഇനി ചോദിക്കാന്‍ ഇടയുള്ളതുമായ പ്രധാന ചോദ്യങ്ങളും അവയുടെ മറുപടികളുമാണു് താഴെ.

1. ഇതൊരു പഞ്ചാംഗമാണോ?
   തിഥി, നക്ഷത്രം, വാരം, യോഗം, കരണം എന്നിവ അടങ്ങിയതാണു പഞ്ചാംഗം. ഇതില്‍ ആദ്യത്തേതു മൂന്നുമുണ്ടു്. അവസാനത്തേതു രണ്ടുമില്ല. അതിനാല്‍ ഇതിനെ പഞ്ചാംഗം എന്നു പറഞ്ഞുകൂടാ. എങ്കിലും ഇതിലുള്ള വിവരങ്ങളില്‍ നിന്നു യോഗവും കരണവും കണ്ടുപിടിക്കാനുള്ള വഴി കേരളപഞ്ചാംഗഗണനം (പേജ് 5, 9, 10) എന്ന പുസ്തകത്തില്‍ വിവരിക്കുന്നുണ്ടു്.

2. ഇതൊരു കലണ്ടറാണോ?
   തീയതികളും മറ്റു വിവരങ്ങളും കൃത്യമായി കൊടുത്തിട്ടുള്ളതുകൊണ്ടു് (A calendar is a system of organizing days for a socially, religious, commercially, or administratively useful purpose എന്നു വിക്കിപീഡിയ.) ഇതൊരു കലണ്ടറാണെന്നു പറയാം. എന്നാല്‍ വര്‍ണ്ണശബളമായ ചിത്രങ്ങളോടു കൂടിയോ അല്ലാതയോ ഓരോ മാസത്തെയും ആഴ്ച തിരിച്ചു പട്ടികയാക്കി കാണിച്ചു ഭിത്തിയില്‍ തൂങ്ങുന്ന സാധനം എന്ന അര്‍ത്ഥത്തില്‍ ഇതു കലണ്ടറല്ല.

3. ഈ കുന്ത്രാണ്ടം ഉണ്ടാക്കാന്‍ എന്താണു പ്രചോദനം?
   കലണ്ടര്‍, ആഴ്ച, തീയതി, നക്ഷത്രം, തിഥി തുടങ്ങിയവ പണ്ടേ എനിക്കു താത്പര്യമുള്ള വിഷയങ്ങളായിരുന്നു. അമേരിക്കയില്‍ വെച്ചു് പിറന്നാള്‍ എന്നാഘോഷിക്കണം, ഇവിടെ ജനിക്കുന്ന കുട്ടിയുടെ നക്ഷത്രമെന്താണു്, രാഹുകാലം എപ്പോള്‍ നോക്കണം, ഷഷ്ഠി, പ്രദോഷം തുടങ്ങിയ വ്രതങ്ങള്‍ എന്നാണു നോക്കേണ്ടതു് തുടങ്ങിയ ചോദ്യങ്ങള്‍ക്കു മറുപടി പറഞ്ഞുകൊടുക്കുന്നതിനോടൊപ്പം മാതൃഭൂമി കലണ്ടര്‍ നോക്കി ഈ സമയങ്ങള്‍ എങ്ങനെ അമേരിക്കന്‍ സമയത്തിലേക്കു മാറ്റി ഇവ കണ്ടുപിടിക്കും എന്നു മനുഷ്യര്‍ക്കു പറഞ്ഞുകൊടുത്തതൊക്കെ അവര്‍ ഒരു ചെവിയിലൂടെ അകത്തേയ്ക്കെടുത്തു് മറുചെവിയിലൂടെ പുറത്തേയ്ക്കു കളഞ്ഞു് അടുത്ത തവണയും അതേ ചോദ്യവുമായി വരുന്നതില്‍ മനം നൊന്തു് എല്ലാവര്‍ക്കുമായി ഉണ്ടാക്കിയതാണു് ഇതു്.

   ആദ്യം ഇംഗ്ലീഷിലായിരുന്നു. മലയാളത്തിലാക്കാന്‍ പ്രചോദനം രാജേഷ് വര്‍മ്മയാണു്. ശ്രീ എ. ജെ. അലക്സ് സരോവര്‍ പോര്‍ട്ടലില്‍ ഇട്ടിരുന്ന LaTeX മലയാളം പാക്കേജ് ഉപയോഗിച്ചു മലയാളം ഉണ്ടാക്കുന്ന ഒരു വിദ്യ അറിയാമായിരുന്നു. വരമൊഴിയെയും ബ്ലോഗുകളെയും യൂണിക്കോഡിനെയും ഒക്കെ പരിചയപ്പെടുന്നതിനു മുമ്പാണു സംഭവം. ഒരു കമ്പ്യൂട്ടര്‍ പ്രോഗ്രാമില്‍ നിന്നു LaTeX സോഴ്സ് ഉണ്ടാക്കാന്‍ പറ്റുമെന്നതിനാല്‍ ഇതിനെ ഒരു പ്രോഗ്രാമിലൊതുക്കാനും പറ്റി.

   പിന്നെ, ബ്ലോഗു തുടങ്ങിയപ്പോള്‍ എല്ലാക്കൊല്ലവും ഇതു പ്രസിദ്ധീകരിക്കാനും തുടങ്ങി.

4. 10 മുതല്‍ 21 വരെയുള്ള പേജുകളില്‍ ഉള്ള പട്ടികകള്‍ എങ്ങനെയാണു് ഉപയോഗിക്കുക?
   ആദ്യത്തെ മൂന്നു കോളങ്ങളില്‍ ഇംഗ്ലീഷ്, മലയാളം, ശകവര്‍ഷത്തീയതികളെ സൂചിപ്പിക്കുന്നു. പിന്നെ ആഴ്ച. അടുത്ത രണ്ടു കോളങ്ങളില്‍ നക്ഷത്രവും തിഥിയും. പിന്നെ ഉദയവും അസ്തമയവും. അതിനു ശേഷം രാഹുകാലം.

   പട്ടികയ്ക്കു താഴെ ഏകാദശി, പ്രദോഷം, ഷഷ്ഠി എന്നീ വ്രതങ്ങളുടെ ദിവസങ്ങള്‍ കൊടുത്തിരിക്കുന്നു. മുകളില്‍ മാസങ്ങള്‍, സംക്രമസമയം തുടങ്ങിയ വിവരങ്ങളും.

   

5. 10 മുതല്‍ 21 വരെയുള്ള പേജുകളില്‍ ഉള്ള പട്ടികകള്‍ ഉപയോഗിച്ചു നക്ഷത്രവും തിഥിയും എങ്ങനെ കണ്ടുപിടിക്കും?
   ഒരു നക്ഷത്രത്തില്‍ നിന്നു മറ്റൊന്നിലേക്കു മാറുന്നതു ദിവസത്തിനിടയിലായിരിക്കും. അതുകൊണ്ടു് രണ്ടും ഇടയില്‍ / ഇട്ടു കാണിച്ചിരിക്കുന്നു. ആദ്യത്തേതില്‍ നിന്നു രണ്ടാമത്തേതിലേക്കു മാറുന്ന സമയവും കാണിച്ചിട്ടുണ്ടാവും. ഒരു ദിവസത്തില്‍ ഒന്നിലധികം തവണ മാറുന്നുണ്ടെങ്കില്‍ രണ്ടു വരികളിലായി കൊടുത്തിട്ടുണ്ടാവും.

   സൂര്യോദയസമയത്തെ നക്ഷത്രവും തിഥിയും കട്ടിയുള്ള അക്ഷരത്തില്‍ കൊടുത്തിരിക്കുന്നു. ഇതു മാത്രമേ സാധാരണ കലണ്ടറുകള്‍/പഞ്ചാംഗങ്ങള്‍ കൊടുക്കാറുള്ളൂ.

   ഉദാഹരണമായി കോഴിക്കോട്ടെ പഞ്ചാംഗത്തില്‍ 2008 ജനുവരി 4 നോക്കുക. (പേജ് 10, പട്ടിക 1 2.1.) 2008 ജനുവരി 4. 1183 ധനു 19. 1929 പൌഷം 14. വെള്ളിയാഴ്ച. സൂര്യോദയത്തിനു നക്ഷത്രം വിശാഖം. ഉച്ചയ്ക്കു 2:23-നു വിശാഖത്തില്‍ നിന്നു് അനിഴമാകും. സൂര്യോദയത്തിനു തിഥി കറുത്ത പക്ഷത്തിലെ ഏകാദശി. രാവിലെ 10:06-നു ദ്വാദശിയാകും. സൂര്യോദയം 6:50-നു്. അസ്തമയം 6:12-നു്. രാഹുകാലം 11:06 മുതല്‍ 12:31 വരെ.

6. വെള്ളിയാഴ്ച രാഹുകാലം രാവിലെ പത്തര മുതല്‍ പന്ത്രണ്ടു വരെ എന്നാണല്ലോ മാതൃഭൂമി കലണ്ടറില്‍.
   സൂര്യന്‍ ആറു മണിക്കുദിച്ചു് ആറു മണിക്കസ്തമിച്ചാല്‍ പത്തര മുതല്‍ പന്ത്രണ്ടു വരെയാണു്. ഉദയാസ്തമയങ്ങള്‍ അനുസരിച്ചു് കാലങ്ങളും മാറും. ഈ ദിവസം 6:50-നു് ഉദിച്ചു് 6:12-നു് അസ്തമിക്കുന്നതുകൊണ്ടു കാലങ്ങളും അതിനനുസരിച്ചു മാറും. വിശദവിവരങ്ങള്‍ കേരളപഞ്ചാംഗഗണനം എന്ന പുസ്തകത്തില്‍ പതിനൊന്നാം പേജിലുണ്ടു്. മറ്റു സ്ഥലങ്ങളില്‍ ഇതു വ്യത്യസ്തമായിരിക്കും.

7. ഈ രാഹുകാലം എന്നൊക്കെ പറയുന്നതു് അന്ധവിശ്വാസമല്ലേ? പിന്നെ എന്തിനാണു് അതല്ല ഇതാണു ശരി എന്നു പറയുന്നതു്?
   രാഹുകാലം അന്ധവിശ്വാസമല്ല. അതൊരു സമയനിര്‍ണ്ണയോപാധിയാണു്. രാഹുകാലം തുടങ്ങിയ കാലങ്ങള്‍ നോക്കി ചെയ്യുന്ന പ്രവൃത്തികള്‍ക്കു ഗുണദോഷങ്ങള്‍ ഉണ്ടു് എന്നു പറയുന്നതാണു് അന്ധവിശ്വാസം.

   ജ്യോതിഷം എന്ന “ശാസ്ത്ര”ത്തെ ശരിയെന്നു കരുതുന്നവരും ഇതൊന്നും ശരിയായി കലണ്ടറുകളിലും പഞ്ചാംഗങ്ങളിലും കാണിക്കാറില്ലെന്നും, ശരാശരി മാത്രം കാണിച്ചാലും ഈ വ്യത്യാസത്തിന്റെ വിശദവിവരങ്ങള്‍ വ്യക്തമാക്കാറില്ല എന്നും വ്യക്തമാക്കാന്‍ കൂടിയാണു് ഇതിവിടെ ഉള്‍ക്കൊള്ളിച്ചിരിക്കുന്നതു്.

8. ഇതില്‍ രാഹുകാലമേ ഉള്ളല്ലോ. ഗുളികകാലം, യമകണ്ടകകാലം തുടങ്ങിയവ എങ്ങനെ കണ്ടുപിടിക്കും?
   കേരളപഞ്ചാംഗഗണനം എന്ന പുസ്തകത്തില്‍ പതിനൊന്നാം പേജു നോക്കി ഉദയാസ്തമയങ്ങളില്‍ നിന്നു കണക്കുകൂട്ടുക.

9. 24-ാ‍ം പേജു മുതല്‍ 35-ാ‍ം പേജു വരെയുള്ള പട്ടികകള്‍ എങ്ങനെ ഉപയോഗിക്കാം?
   ഓരോ ദിവസവും തുടങ്ങുമ്പോഴുള്ള (അര്‍ദ്ധരാത്രി) ഗ്രഹസ്ഫുടമാണു് അതിലുള്ളതു്. ഉദാഹരണമായി ഇന്ത്യന്‍ സ്റ്റാന്‍ഡേര്‍ഡ് ടൈം 2008 ജനുവരി 1-നു മുമ്പുള്ള അര്‍ദ്ധരാത്രിയ്ക്കു സൂര്യന്‍ ധനു 15:43, ചന്ദ്രന്‍ കന്നി 20:34, ചൊവ്വ മിഥുനം 5:58, ബുധന്‍ ധനു 23:56, വ്യാഴം ധനു 9:4, ശുക്രന്‍ വൃശ്ചികം 7:16, ശനി ചിങ്ങം 14:36, രാഹു കുംഭം 6:22, കേതു ചിങ്ങം 6:22.

   

10. കുജന്‍, ശനി, രാഹു, കേതു എന്നിവയുടെ സ്ഫുടം കട്ടിയുള്ള അക്ഷരത്തിലാണല്ലോ.
    അവ വക്രം (retrograde) ആണെന്നാണു് അര്‍ത്ഥം. ഭൂമിയില്‍ നിന്നു നോക്കുമ്പോള്‍ അവ പുറകോട്ടു പോകുന്നതായി തോന്നുന്നു എന്നര്‍ത്ഥം. ഇതെന്തുകൊണ്ടാണെന്നു് (സൂര്യനെ ചുറ്റി ഭൂമിയുള്‍പ്പെടെയുള്ള ഗ്രഹങ്ങള്‍ സഞ്ചരിക്കുന്നതുകൊണ്ടു്) പണ്ടുള്ളവര്‍ക്കു് അറിയാന്‍ പാടില്ലാത്തതിനാല്‍ അധിവൃത്തങ്ങളുടെ ഒരു തിയറി ഉണ്ടാക്കുകയും വക്രനായാല്‍ ഒരു ഗ്രഹത്തിന്റെ ബലം വിപരീതമാകുകയോ കുറയുകയോ ചെയ്യുമെന്നും പറഞ്ഞു.

    സൂര്യനും ചന്ദ്രനും ഒരിക്കലും വക്രമാവില്ല. (കാരണം നമുക്കറിയാം. സൂര്യനെ ഭൂമിയും ഭൂമിയെ ചന്ദ്രനും ഒരേ ദിശയില്‍ത്തന്നെ ചുറ്റുന്നു.) സൂര്യ-ചന്ദ്രപഥങ്ങളുടെ സംഗമബിന്ദുക്കള്‍ എപ്പോഴും പുറകോട്ടു പോകുന്നതു കൊണ്ടു് രാഹുവും കേതുവും എപ്പോഴും വക്രന്മാരാണു്. ബാക്കി എല്ലാ ഗ്രഹങ്ങളും വക്രമാവാം. ഇതൊക്കെ ജ്യോതിഷപുസ്തകങ്ങളില്‍ പ്രത്യേകനിയമങ്ങളായി കൊടുത്തിട്ടുണ്ടു്. ചില “കാരണങ്ങളും” പറഞ്ഞിട്ടുണ്ടു്.

11. അര്‍ദ്ധരാത്രിയല്ലാത്ത സമയത്തിന്റെ സ്ഫുടം എങ്ങനെ കണ്ടുപിടിക്കും?
    Linear interpolation ഉപയോഗിക്കുക. ഇതില്‍ കൂടുതല്‍ granularity കൊടുക്കാന്‍ നിവൃത്തിയില്ല. പഞ്ചാംഗങ്ങളില്‍ 10 ദിവസങ്ങളിലൊരിക്കല്‍ ഉള്ള സ്ഫുടമേ ഉള്ളൂ എന്നും ഓര്‍ക്കുക.

12. യുറാനസ്, നെപ്റ്റ്യൂണ്‍, പ്ലൂട്ടോ എന്നിവ കാണുന്നില്ലല്ലോ? 🙂
    36-ാ‍ം പേജില്‍ അതുമുണ്ടു്. മാസത്തില്‍ രണ്ടു പ്രാവശ്യമേ ഉള്ളൂ എന്നു മാത്രം. ആര്‍ക്കെങ്കിലും വേണമെങ്കില്‍ എടുക്കാം 🙂

13. എന്താണു ലഗ്നം? 38 മുതല്‍ 49 വരെയുള്ള പേജുകളിലെ ടേബിളുകള്‍ എന്തിനാണു്?
    ഒരു സ്ഥലത്തിന്റെ കൃത്യം കിഴക്കുഭാഗത്തു് ഒരു പ്രത്യേക സമയത്തു് ഉള്ള രാശിയാണു ലഗ്നം (Ascendant). രാശി എന്നതുകൊണ്ടു് ഒരു ബിന്ദുവിനെ അടിസ്ഥാനമാക്കിയുള്ള ആംഗിള്‍ എന്നു കരുതിയാല്‍ മതി. ഇതു് ഓരോ സ്ഥലത്തിനും (ഒരേ ടൈം സോണിലുള്ളവയ്ക്കും) വ്യത്യസ്തമായിരിക്കും.

    ഇതു ജ്യോതിഷത്തില്‍ മാത്രമുപയോഗിക്കുന്ന ഒരു കാര്യമാണു്. സാധാരണ ആവശ്യമുള്ളതല്ല.

14. ഇവയിലെ ആദ്യത്തെ സെറ്റ് ടേബിളുകളേ സാധാരണ ആവശ്യമുള്ളൂ. ഇതു മൂന്നു ഡോക്യുമെന്റ് ആയി പ്രസിദ്ധീകരിച്ചുകൂടേ? എല്ലാം കൂടി പ്രിന്റ് ചെയ്യണ്ടല്ലോ.
    അക്രോബാറ്റ് റീഡറില്‍ പറയുന്ന പേജുകള്‍ മാത്രം പ്രിന്റു ചെയ്യാനുള്ള വകുപ്പുണ്ടല്ലോ.

    ടേബിളുകള്‍ പുനഃക്രമീകരിക്കണമെന്നു് ആഗ്രഹമുണ്ടു്. ഒരേ ടൈം സോണിലുള്ളവയ്ക്കു പൊതുവായുള്ളതു വേറെയും വ്യത്യസ്തമായതു വേറെയും എന്നിങ്ങനെ. മുസ്ലീം നമസ്കാരസമയം തുടങ്ങിയവയും അതിനോടൊപ്പം ചേര്‍ക്കാം.

15. നക്ഷത്രവും മറ്റും മാറുന്ന സമയം സാധാരണ കലാണ്ടറുകളില്‍ കാണുന്നതില്‍ നിന്നു വ്യത്യാസമുണ്ടല്ലോ, ഞാന്‍ കോഴിക്കോട്ടേ പഞ്ചാംഗം നോക്കിയിട്ടും?
    സാധാരണ കലണ്ടറുകളിലും പഞ്ചാംഗങ്ങളിലും ഉദയാല്‍പ്പരനാഴികയാണു കൊടുക്കുക. അതായതു്, സൂര്യോദയത്തിനു ശേഷം എത്ര നാഴിക (1 നാഴിക = 24 മിനിട്ടു് = 60 വിനാഴിക) കഴിഞ്ഞാണെന്നു്.

    ഉദാഹരണമായി, 2008 ജനുവരി 2-നു കോഴിക്കോട്ടു് ഉദയം 6:49-നാണു്. ചിത്തിര നക്ഷത്രം ചോതിയാകുന്നതു് 8:26-നാണു്-അതായതു് ഉദയം കഴിഞ്ഞു് 97 മിനിറ്റ് കഴിഞ്ഞു്, അതായതു് 97/24 = 4.041666… നാഴിക കഴിഞ്ഞു്. അതായതു് 4 നാഴിക 2.5 വിനാഴിക കഴിഞ്ഞു്. കലണ്ടറുകളില്‍ 4:2 എന്നോ 4:3 എന്നോ കാണാം.

    സൂര്യോദയത്തിനു നാഴികവട്ട സജ്ജീകരിച്ചു് അതിനെ നോക്കി സമയം കണ്ടുപിടിക്കുന്ന രീതി ഇപ്പോഴും തുടരുന്നതു് എന്തിനാണെന്നറിയില്ല. കലണ്ടറിലെ സമയം കണ്ടുപിടിക്കാന്‍ ആളുകള്‍ക്കു് ഇപ്പോള്‍ അന്നത്തെ സൂര്യോദയം കണ്ടുപിടിച്ചു് അതു കുറച്ചു് മണിക്കൂര്‍/മിനിട്ടു് ആക്കണം.

16. ചില ജ്യോതിഷകാര്യങ്ങള്‍ക്കു് ഉദയാല്‍പ്പരനാഴിക തന്നെ വേണമെന്നു കേള്‍ക്കുന്നല്ല്ലോ.
    ലഗ്നം കണ്ടുപിടിക്കാനുള്ള ഭാരതീയരീതിയ്ക്കാണു് അതു വേണ്ടതു്. ഈ പഞ്ചാംഗത്തില്‍ ലഗ്നത്തിനു വേറേ പട്ടികകളുണ്ടു്. ഇനി ഉദയാല്‍പ്പരനാഴിക കണ്ടുപിടിക്കണമെങ്കില്‍ത്തന്നെ മുകളില്‍ കൊടുത്തിരിക്കുന്ന രീതിയില്‍ കണക്കു കൂട്ടി കണ്ടുപിടിക്കാം.

17. ജ്യോതിഷത്തിനു ശാസ്ത്രീയാടിസ്ഥാനമുണ്ടോ?
    ശാസ്ത്രീയമായ പഠനങ്ങള്‍ കാണിക്കുന്നതു സംഭാവ്യതാശാസ്ത്രം തരുന്നതില്‍ കൂടുതല്‍ ഫലമൊന്നും ജ്യോതിഷത്തിന്റെ പ്രവചനങ്ങള്‍ക്കില്ല എന്നാണു്. അതിനാല്‍ ശാസ്ത്രീയാടിസ്ഥാനം ഇല്ലെന്നു തന്നെ പറയേണ്ടി വരും.

18. എന്റെ സ്ഥലത്തിന്റെ പഞ്ചാംഗം ഈ ലിസ്റ്റിലില്ലല്ലോ. എന്തു ചെയ്യും?
    അടുത്തുള്ളതും അതേ ടൈം‌സോണിലുള്ളതുമായ ഏതെങ്കിലും സ്ഥലത്തിന്റെ പഞ്ചാംഗം കൊണ്ടു് തത്ക്കാലം അഡ്‌ജസ്റ്റു ചെയ്യൂ. കോഴിക്കോട്ടോ കോട്ടയത്തോ ഗണിച്ച കലണ്ടര്‍ കൊണ്ടു മലയാളികള്‍ മുഴുവന്‍ അഡ്ജസ്റ്റു ചെയ്യുന്നില്ലേ?

    അതു പോരാ എന്നുണ്ടെങ്കില്‍ ഏതു സ്ഥലത്തിന്റെ പഞ്ചാംഗം വേണമെന്നു കാണിച്ചു് ഒരു കമന്റിടുക. ഉമേഷ്.പി.നായര്‍ അറ്റ് ജീമെയില്‍.കോം എന്ന വിലാസത്തില്‍ ഒരു മെയിലയച്ചാലും മതി.

19. ഭൂമിയിലുള്ള ഏതു സ്ഥലത്തിന്റെയും പഞ്ചാംഗം ഗണിക്കാന്‍ പറ്റുമോ?
    പറ്റില്ല. ഇതിലെ പലതും കണ്ടുപിടിക്കുന്നതിനു് ആ ദിവസത്തെ സൂര്യോദയാസ്തമയങ്ങള്‍ ആവശ്യമാണു്. ആറുമാസത്തേയ്ക്കു സൂര്യന്‍ ഉദിക്കുകയോ അസ്തമിക്കുകയോ ചെയ്യാത്ത ആര്‍ട്ടിക് സര്‍ക്കിളിനു വടക്കുള്ളതോ അന്റാര്‍ട്ടിക് സര്‍ക്കിളിനു തെക്കുള്ളതോ ആയ സ്ഥലങ്ങള്‍ക്കു് ഈ ക്രിയകള്‍ എങ്ങനെ ചെയ്യും എന്നു് എനിക്കറിയില്ല.

    നോര്‍വ്വേ, സ്വീഡന്‍, ഫിന്‍ലാന്‍ഡ്, റഷ്യ, അമേരിക്ക (അലാസ്ക സ്റ്റേറ്റ്), കാനഡ, ഗ്രീന്‍‌ലാന്‍ഡ്, ഐസ്‌ലാന്‍ഡ് എന്നീ രാജ്യങ്ങളില്‍ മാത്രമേ ആര്‍ട്ടിക് സര്‍ക്കിളിന്റെ വടക്കു മനുഷ്യവാസമുള്ളൂ. അന്റാര്‍ട്ടിക് സര്‍ക്കിളിനു തെക്കു് അന്റാര്‍ട്ടിക്ക മാത്രമേ ഉള്ളൂ.

20. ഞാന്‍ ഫിന്‍ലാന്‍ഡില്‍ താമസിക്കുന്ന ഒരു ബ്ലോഗസഹോദരനാണു്. എനിക്കിവിടെ ആറു മാസം പകലും ആറു മാസം രാത്രിയുമാണു്. എന്റെ പ്രിയപ്പെട്ട ബ്ലോഗസഹോദരനു പിറന്നാള്‍ ആശംസകള്‍ ഫോണില്‍ വിളിച്ചു് അര്‍പ്പിക്കുന്നതെങ്ങനെയെന്നു പറഞ്ഞുതരാമോ?
    ആര്‍ട്ടിക് സര്‍ക്കിളിനു തെക്കുള്ള ഹെല്സിങ്കിയിലെ പഞ്ചാംഗം വേണമെങ്കില്‍ ഉണ്ടാക്കിത്തരാം. അല്ലെങ്കില്‍ അതേ ടൈം‌സോണിലുള്ള ഏതെങ്കിലും പഞ്ചാംഗം നോക്കി പിറന്നാളിന്റെ തീയതി കണ്ടുപിടിച്ചു വിളിച്ചാല്‍ മതി.

    സൂര്യോദയത്തിനു് നക്ഷത്രം വരുന്ന ദിവസമാണു് പിറന്നാളായി ആഘോഷിക്കുന്നതു്. ഈ പഞ്ചാംഗത്തില്‍ അതു കട്ടിയുള്ള അക്ഷരത്തില്‍ കൊടുത്തിരിക്കുന്നു.

    പിന്നെ, തലയില്‍ ഒരു രോമമെങ്കിലുമുള്ളവരുടെ മാത്രമേ പിറന്നാള്‍ ആഘോഷിക്കാറുള്ളൂ 🙂

21. ഞാന്‍ ഇന്ത്യ, ജപ്പാന്‍, യൂറോപ്പ്, അമേരിക്ക തുടങ്ങിയ സ്ഥലങ്ങളില്‍ ഒരു ജിടെന്‍ഷാ അഥവാ സൈക്കിളില്‍ പര്യടനം നടത്തുന്ന ഒരു സഞ്ചാരിയാണു്. ഞാന്‍ ഇപ്പോള്‍ എവിടെയാണെന്നു പറയാന്‍ എനിക്കു മനസ്സില്ല. എനിക്കു ഷഷ്ഠി, ഏകാദശി തുടങ്ങിയ വ്രതങ്ങള്‍ അനുഷ്ഠിക്കാന്‍ ഏതു പഞ്ചാംഗമാണു നോക്കേണ്ടതു്?
    യാത്ര ചെയ്യുമ്പോള്‍ വ്രതം നോക്കാന്‍ പഞ്ചാംഗം നോക്കണ്ടാ സഞ്ചാരീ. എവിടെയാണെന്നു പറയാന്‍ മനസ്സില്ലെങ്കില്‍ ഈ ചോദ്യത്തിനു് ഉത്തരം പറയാന്‍ എനിക്കും മനസ്സില്ല.

22. ഇന്ത്യ, അമേരിക്ക, ഉഗാണ്ടാ, കൊളംബിയ, ഇറ്റലി, അന്റാര്‍ട്ടിക്ക തുടങ്ങിയ സ്ഥലങ്ങളില്‍ ഓരോ ആഴ്ചയും മാറിമാറി താമസിക്കുന്ന ഒരു ക്രിസ്ത്യാനിപ്പെണ്ണാണു ഞാന്‍. ഓരോ ആഴ്ചയിലും പേരും മാറ്റാറുണ്ടു്. എല്ലാ ക്ഷാരബുധനും, ദുഃഖവെള്ളിയാഴ്ചയ്ക്കും ക്രിസ്തുമസ്സിനും ഞാന്‍ ഓരോ ബ്ലോഗ് ഡിലീറ്റ് ചെയ്തു ബലിയര്‍പ്പിക്കാറുണ്ടു്. ഈ ദിവസങ്ങള്‍ കണ്ടുപിടിക്കാന്‍ ഞാന്‍ ഏതു പഞ്ചാംഗമാണു നോക്കേണ്ടതു്?
    ക്രിസ്തുമസ് എല്ലാക്കൊല്ലവും എല്ലാ പഞ്ചാംഗത്തിലും ഡിസംബര്‍ 25 ആണു്. ബാക്കിയുള്ളവ മാറും. എങ്കിലും ഒരു പ്രത്യേക വര്‍ഷത്തില്‍ അവയെല്ലാം നിശ്ചിതതീയതിയിലായിരിക്കും. അതുകൊണ്ടു് ഏതെങ്കിലും പഞ്ചാംഗം നോക്കിയാല്‍ മതി.
    എവിടെയായാലും 2008-ല്‍ ക്ഷാരബുധന്‍ ഫെബ്രുവരി 6, ദുഃഖവെള്ളിയാഴ്ച മാര്‍ച്ച് 21, ക്രിസ്തുമസ് ഡിസംബര്‍ 25. ഈ തീയതികളില്‍ ബ്ലോഗ് ഡിലീറ്റ് ചെയ്തുകൊള്ളൂ.

23. ഇതു മൊത്തം തെറ്റാണു ചേട്ട. ക്രിസ്തുമസ് ഡിസംബര്‍ 25 അല്ല. ഗാന്ധിജയന്തി വിശേഷദിവസമായി കാണിക്കാന്‍ തക്ക മഹാത്മാവല്ല ഗാന്ധി. അമേരിക്കാ‍ാ‍ാ‍ാ‍ായിലെ താങ്ക്സ് ഗിവിംഗുമൊക്കെ മലയാളം പഞ്ചാങ്കത്തില്‍ എന്തരു കാട്ടണതു്?
    പോപ്പുലറായ കുറച്ചു വിശേഷദിവസങ്ങളാണു് ഇതിലുള്ളതു്. സമഗ്രമെന്നു് അവകാശപ്പെടുന്നില്ല. പല വിശേഷദിവസങ്ങളും ശരിയായ ദിവസത്തിലല്ല ആഘോഷിക്കുന്നതെന്നറിയാം. എങ്കിലും പൊതുവേ ഉപയോഗിച്ചു വരുന്ന തീയതികളാണു് ഇതില്‍ കാണുക.

    ഇതിന്റെ വലിയൊരു പങ്ക് ഉപഭോക്താക്കള്‍ അമേരിക്കയിലുള്ളവരാണു്. അതുകൊണ്ടാണു് അമേരിക്കന്‍ വിശേഷദിവസങ്ങളും ഉള്‍ക്കൊള്ളിച്ചതു്.

24. ഇതു മൊത്തം ആസ്കി ഫോണ്ടാണല്ലോ. ഈ മല്ല്ലുക്കളോടു പറഞ്ഞു മടുത്തു. എത്ര പറഞ്ഞാലും നീയൊന്നും യൂണിക്കോട് ഉപയോഗിക്കുകയില്ല എന്നുറച്ചിരിക്കുകയാണോ? നിന്നെയൊക്കെ വേലിപ്പത്തലൂരി മുക്കാലിയില്‍ കെട്ടി അടിക്കണം.
    യൂണിക്കോഡിനെപ്പറ്റി അറിയാത്ത കാലത്തു് ഉണ്ടാക്കിയതാണിതു്. PDF-ല്‍ യൂണിക്കോഡ് അല്പം ബുദ്ധിമുട്ടുമാണു്. ഈയിടെ ഒരു ലാറ്റക് മലയാളം/ഒമേഗ പാക്കേജ് http://malayalam.sarovar.org/-ല്‍ കണ്ടു. അതു് ഉപയോഗിച്ചു തുടങ്ങുന്നതേ ഉള്ളൂ. അതു ശരിയായി ഉപയോഗിക്കാന്‍ പഠിച്ചാല്‍ ഇതും യൂണിക്കോഡിലാക്കാം.

25. ബാംഗ്ലൂരില്‍ നിന്നും അമേരിക്കയിലെ മിനസോട്ടയിലേക്കു കുടിയേറിപ്പാര്‍ത്ത ഒരു രണ്ടക്ക-ഐക്യു ബ്ലോഗറാ‍ണു ഞാന്‍. ഞാന്‍ എവിടെപ്പോയാലും അവിടെ അത്യാഹിതം സംഭവിക്കും. ഒരു പാലത്തിന്റെ പടമെടുത്താ‍ല്‍ അതു പൊളിയും. വെക്കേഷനു പോകുന്ന സ്ഥലത്തു തീപിടിത്തമുണ്ടാവും. യാത്ര തുടങ്ങുമ്പോള്‍ രാഹുകാലം നോക്കാത്തതുകൊണ്ടാണു് ഇങ്ങനെ സംഭവിക്കുന്നതു് എന്നു് ബാംഗ്ലൂരുള്ള ഒരു മുന്‍ കമ്യൂണിസ്റ്റ് നേതാവു പറഞ്ഞു. ഇതു ശരിയാണോ?
    ശരിയല്ല. രാഹുകാലം നോക്കുന്നതു് ഒരു അന്ധവിശ്വാസമാണു്. അതു നോക്കുന്നതുകൊണ്ടോ നോക്കാത്തതു കൊണ്ടോ ഒരു വ്യത്യാസവും ഉണ്ടാവുകയില്ല.

26. രാഹുകാലം, ഗ്രഹസ്ഫുടങ്ങള്‍, ലഗ്നം ഇവയൊക്കെ കൊടുക്കുന്നതുകൊണ്ടു് താങ്കള്‍ അന്ധവിശ്വാസങ്ങളെ പ്രോത്സാഹിപ്പിക്കുകയല്ലേ?
    ഞാന്‍ ഇവയുടെ സമയം കണക്കുകൂട്ടി കൊടുക്കുക മാത്രമാണു ചെയ്യുന്നതു്. അല്ലാതെ ആ സമയങ്ങള്‍ക്കു് എന്തെങ്കിലും പ്രത്യേകതയുണ്ടെന്നോ ആ സമയത്തു ചെയ്യുന്ന കാര്യങ്ങള്‍ക്കു ഗുണമോ ദോഷമോ ഉണ്ടാകും എന്നോ പറയുന്നില്ല. എന്നു മാത്രമല്ല, ഇത്തരം കാര്യങ്ങള്‍ വെറും അന്ധവിശ്വാസമാണെന്ന അഭിപ്രായക്കാരനാണു ഞാന്‍.

    ഞാന്‍ ഇതു പ്രസിദ്ധീകരിക്കുന്നതിനു പല കാരണങ്ങളുണ്ടു്:

    1. മലയാളികളുടെ പല വിശേഷദിവസങ്ങളും (ഓണം, വിഷു, ഈസ്റ്റര്‍ തുടങ്ങിയവ) കണ്ടുപിടിക്കുന്നതു ശ്രമകരമാണു്. ഇവയില്‍ പലതും മതപരമായ കാര്യങ്ങളുമായി ബന്ധപ്പെട്ടു കിടക്കുന്നെങ്കിലും മലയാളിയുടെ സംസ്കാരത്തിന്റെ ഭാഗമാണു്. അവ ആചരിക്കുന്നവര്‍ക്കു്, പ്രത്യേകിച്ചു വിദേശത്തുള്ളവര്‍ക്കു്, ചിന്താക്കുഴപ്പമില്ലാതെ അവരവരുടെ സമയത്തില്‍ അവയെ കാണിക്കുന്നതു പ്രയോജനപ്രദമാകും എന്നു കരുതി.
    2. ജ്യോതിഷപ്രവചനങ്ങള്‍ തെറ്റുമ്പോള്‍ പലപ്പോഴും കണക്കുകൂട്ടലുകള്‍ തെറ്റിയതുകൊണ്ടാണു് അങ്ങനെ സംഭവിച്ചതു് എന്നൊരു വാദം കേള്‍ക്കാറുണ്ടു്. അത്തരം സന്ദര്‍ഭങ്ങളില്‍ കൃത്യമായ കണക്കുകൂട്ടലുകള്‍ പരിശോധിക്കാനുള്ള ഒരു സംവിധാനം ഇതു നല്‍കുന്നു. ആധുനികജ്യോതിശ്ശാസ്ത്രം (astronomy) ഉപയോഗിച്ചു ഗ്രഹങ്ങളുടെ സ്ഥാനം കണ്ടുപിടിക്കുന്നതിനോടൊപ്പം ഭാരതീയജ്യോതിഷത്തിലെ നക്ഷത്രം, തിഥി, ലഗ്നം തുടങ്ങിയവയും കൃത്യമായി കണ്ടുപിടിക്കുന്നു. ജ്യോത്സ്യന്മാര്‍ സാധാരണയായി ഉപയോഗിക്കുന്ന ത്രൈരാശികം (linear interpolation) എന്ന ഏകദേശക്കണക്കിനു പകരം സൂക്ഷ്മമായ iterative algorithms ഉപയോഗിച്ചാണു് സങ്കീര്‍ണ്ണമായ ഗണിതക്രിയകള്‍ ചെയ്യുന്നതു്.
    3. കലണ്ടറുകളില്‍ കാണുന്ന ഉദയാല്‍പ്പരനാഴികയ്ക്കു പകരം ഇന്നു പ്രചാരത്തിലുള്ള ഘടികാരസമയം തന്നെ കാണിക്കുക. Day light savings ഉള്ള സ്ഥലങ്ങളില്‍ അതും കണക്കിലെടുക്കുക.
    4. വ്രതങ്ങളും മറ്റും നോക്കുന്ന വിശ്വാസികള്‍ക്കു് നാട്ടിലെ കലണ്ടറില്‍ നിന്നു സമയം സംസ്കരിച്ചെടുക്കാനുള്ള ബുദ്ധിമുട്ടു്‌ ഒഴിവാക്കാന്‍ ഒരു വഴി.

    ഇവയാണു്, ഇവ മാത്രമാണു്, ഇതിന്റെ ഉദ്ദേശ്യം. അന്ധവിശ്വാസങ്ങളെ പ്രോത്സാഹിപ്പിക്കാനല്ല, എതിര്‍ക്കാ‍ന്‍ തന്നെയാണു് എന്റെ ശ്രമം.

27. അഗ്രഹാരത്തില്‍ ജനിച്ചു് ഇപ്പോഴും പൂജ, കൂടോത്രം, ജ്യോതിഷം, മന്ത്രവാദം എന്നിവ നിത്യേന ചെയ്യുന്ന ഒരു മൂത്ത കമ്മ്യൂണിസ്റ്റ് യുക്തിവാദിനിയാണു ഞാന്‍. എല്ലാ മലയാളമാസം ഒന്നാം തീയതിയും ഞാന്‍ മാര്‍ക്സ്, എംഗത്സ്, ലെനിന്‍, ചെ ഗുവര, ഇ. എം. എസ്. തുടങ്ങിയവരുടെ ആത്മാവിനു നിത്യശാന്തി കിട്ടാന്‍ പൊങ്കാലയിടാറുണ്ടു്. പക്ഷേ, നാട്ടിലെ കലണ്ടറില്‍ കാണുന്ന ദിവസമല്ല ഈ പഞ്ചാംഗത്തില്‍ ഒന്നാം തീയതി. ഏതു ദിവസമാണു ഞാന്‍ ഉപയോഗിക്കേണ്ടതു്?
    സൂര്യന്‍ ഒരു രാശി(മാസം)യില്‍ നിന്നു് അടുത്ത രാശിയിലേക്കു മാറുന്ന നിമിഷം (സംക്രമം) ഒരു പകലിന്റെ അഞ്ചില്‍ മൂന്നു ഭാഗം കഴിയുന്നതിനു മുമ്പാണെങ്കില്‍ അതേ ദിവസവും, ശേഷമാണെങ്കില്‍ പിറ്റേ ദിവസവും ആണു് രണ്ടാമത്തെ മാസത്തിലെ ഒന്നാം തീയതി എന്നാണു കണക്കു്. (വടക്കേ മലബാര്‍ കണക്കനുസരിച്ചു് എപ്പോഴും പിറ്റേ ദിവസമാണു് ഒന്നാം തീയതി. അതു് ഇവിടെ കൊടുത്തിട്ടില്ല. മാതൃഭൂമി കലണ്ടറില്‍ അതുണ്ടു്.) എന്റെ പഞ്ചാംഗത്തില്‍ അതാതു സ്ഥലത്തെ ഉദയം നോക്കിയിട്ടു് ഞാന്‍ ഈ നിയമം ഉപയോഗിച്ചു് ഒന്നാം തീയതി കണ്ടുപിടിക്കുന്നു. ഇതു നാട്ടിലെ കലണ്ടറുമായി ഗ്രിഗോറിയന്‍ കലണ്ടറിലെ തീയതിയില്‍ വ്യത്യാസമുണ്ടാവാം.

    ഇങ്ങനെ തന്നെ വേണോ കൊല്ലവര്‍ഷകലണ്ടര്‍ തയ്യാറാക്കാന്‍, അതോ കേരളത്തിലെ ഏതെങ്കിലും സ്ഥലത്തെ അടിസ്ഥാനമാക്കി വേണോ എന്നതിനെപ്പറ്റി ആരും ആധികാരികമായി എഴുതിയിട്ടില്ല. അതിനാല്‍ ഞാന്‍ എനിക്കു ശാസ്ത്രീയമെന്നു തോന്നിയ ഈ രീതി ഉപയോഗിക്കുന്നു.

28. ഇതില്‍ ബക്രീദ്, റംസാന്‍ തുടങ്ങിയ മുസ്ലീം വിശേഷദിവസങ്ങള്‍ ഇല്ലല്ലോ. ഹിജ്ര വര്‍ഷത്തീയതിയും ഇല്ല.
    ഇസ്ലാമിക് കലണ്ടറിന്റെ കണക്കുകൂട്ടലുകള്‍ കൈവശമുണ്ടെങ്കിലും ഇതു വരെ അതു് ഈ കലണ്ടറില്‍ ഉള്‍ക്കൊള്ളിക്കുവാന്‍ കഴിഞ്ഞിട്ടില്ല. താമസിയാതെ ചേര്‍ക്കാം എന്നു കരുതുന്നു.

29. രാഹുകാലം പോലെയുള്ള അന്ധവിശ്വാസങ്ങള്‍ ഒഴിവാക്കി മുസ്ലീം നമസ്കാരസമയങ്ങള്‍ ചേര്‍ത്തുകൂടേ?
    രാഹുകാലവും മുസ്ലീം നമസ്കാരസമയവും ഒരുപോലെ തന്നെയുള്ള ആചാരങ്ങളാണു്. രണ്ടും കണ്ടുപിടിക്കുന്നതില്‍ സാമ്യവുമുണ്ടു്. ഓരോ ദിവസത്തിന്റെയും മുസ്ലീം നമസ്കാരസമയവും ചേര്‍ക്കാന്‍ ഉദ്ദേശ്യമുണ്ടു്. പക്ഷേ, ഉയര്‍ന്ന അക്ഷാംശം ഉള്ളിടത്തെ കണക്കുകൂട്ടലില്‍ ഇസ്ലാമിക് പണ്ഡിതന്മാര്‍ക്കു ഭിന്നാഭിപ്രായമുണ്ടു്. അതുപോലെ ചില നിസ്കാരസമയം സമുദായത്തിലെ രണ്ടു വിഭാഗങ്ങള്‍ രണ്ടു വിധത്തിലാണു കണക്കുകൂട്ടുന്നതു്. ഏറ്റവും ശരിയായ തിയറി കിട്ടിയാല്‍ അതും ചേര്‍ക്കാം. ഇതുവരെ എനിക്കറിയാവുന്ന കാര്യങ്ങള്‍ ഇവിടെ ഉണ്ടു്.

30. കേരളത്തിലെ അഞ്ചു സ്ഥലങ്ങളിലെ പഞ്ചാംഗമുണ്ടെങ്കിലും കൊല്ലവര്‍ഷം തുടങ്ങിയ കൊല്ലം നഗരത്തിന്റെ പഞ്ചാംഗമില്ല. ഇതിനെതിരേ മുഖ്യമന്ത്രിയ്ക്കു് ഒരു നിവേദനം സമര്‍പ്പിക്കുകയും ഒരു സെക്രട്ടേറിയേറ്റ് ധര്‍ണ്ണ സംഘടിപ്പിക്കുകയും ചെയ്താലോ എന്നു കരുതുകയാണു്.
    വായനക്കാര്‍ ആവശ്യപ്പെട്ട സ്ഥലങ്ങളിലെ പഞ്ചാംഗങ്ങളാണു് ഇവ. അല്ലാതെ സ്ഥലങ്ങളുടെ പ്രാധാന്യം നോക്കിയുള്ളതല്ല. കൊല്ലത്തിന്റെയോ മറ്റേതെങ്കിലും സ്ഥലത്തിന്റെയോ പഞ്ചാംഗം വേണമെങ്കില്‍ അറിയിക്കുക.

31. പഴയ പഞ്ചാംഗത്തിന്റെ രീതിയിലുള്ള പട്ടികകള്‍ക്കു പകരം ആധുനികകലണ്ടറുകളുടെ രീതിയില്‍ ആഴ്ച തിരിച്ചു് പ്രസിദ്ധീകരിക്കാമോ?
    ഇതിനുപയോഗിക്കുന്ന ലൈബ്രറിയുപയോഗിച്ചു് (ലൈബ്രറി എന്താണെന്നറിയാന്‍ അരവിന്ദന്റെ വികടസരസ്വതി എന്ന കൃതി വായിക്കുക) അതും ഉണ്ടാക്കാന്‍ പറ്റും. കുറച്ചു പണിയുണ്ടെന്നു മാത്രം. ആര്‍ക്കെങ്കിലും താത്പര്യമുണ്ടെങ്കില്‍ അറിയിക്കുക.

32. ഇതു് ഗ്നു ലൈസന്‍സ് ഉപയോഗിച്ചു് സ്വതന്ത്ര സോഫ്റ്റ്വെയര്‍ ആക്കിക്കൂടേ?
    ആക്കണം. അതിനു മുമ്പു് കോഡ് ഒന്നു നേരേ ചൊവ്വേ ആക്കണം. മലയാളം ലാറ്റക് മാത്രം ഉണ്ടാക്കുന്ന API മാറ്റി ഏതു ഫോര്‍മാറ്റിലും customized ആയി ഔട്ട്‌പുട്ട് ഉണ്ടാക്കാവുന്ന രീതിയില്‍ മാറ്റിയെഴുതണം. അത്രയും ചെയ്തു കഴിഞ്ഞാല്‍ സ്വതന്ത്ര സോഫ്റ്റ്വെയറായി പ്രസിദ്ധീകരിക്കും.

33. കേരളീയപഞ്ചാംഗഗണനത്തിനുള്ള algorithms ഒരു ബ്ലോഗ് പോസ്റ്റോ PDF പുസ്തകമോ ആയി പ്രസിദ്ധീകരിച്ചുകൂടേ?
    ആഗ്രഹമുണ്ടു്. കുറെയൊക്കെ എഴുതി വെച്ചിട്ടുമുണ്ടു്. പൂര്‍ത്തിയാക്കാന്‍ പറ്റുമോ എന്നു നോക്കട്ടേ.

34. ഇതില്‍ മാതൃഭൂമിയും മനോരമയും മറ്റും പ്രസിദ്ധീകരിക്കുന്ന കലണ്ടറുകളിലെ എല്ലാ വിവരങ്ങളും ഉണ്ടോ? അവയ്ക്കു പകരം ഇതുപയോഗിച്ചാല്‍ മതിയോ?
    ഇല്ല, പോരാ. അവയില്‍ പല ദേവാലയങ്ങളിലെയും ഉത്സവങ്ങള്‍, പല ആചാരങ്ങളുടെയും തീയതികള്‍, നേതാക്കന്മാരുടെയും മറ്റും ജനന/മരണത്തീയതികള്‍ തുടങ്ങി ധാരാളം വിശേഷദിവസങ്ങള്‍ ചേര്‍ത്തിട്ടുണ്ടു്. പിന്നെ തീവണ്ടിസമയം, STD കോഡുകള്‍ തുടങ്ങിയ വിവരങ്ങളും. അവയൊന്നും ഇതിലില്ല. കൂടാതെ അവയുടെ ഫോര്‍മാറ്റ് അല്പം കൂടി സൌകര്യപ്രദമാണെന്നു മിക്കവരും പറയുന്നു.

    അതേ സമയം, ഇതില്‍ നാളും മറ്റും മാറുന്ന സമയം ഘടികാരസമയമായി കൊടുത്തിരിക്കുന്നതു കൂടുതല്‍ സൌകര്യമാണെന്നു പറയുന്നവരുമുണ്ടു്.

35. ഇതില്‍ മാതൃഭൂമിയും ഗുരുവായൂര്‍ ദേവസ്വവും മറ്റും പ്രസിദ്ധീകരിക്കുന്ന പഞ്ചാംഗങ്ങളിലെ എല്ലാ വിവരങ്ങളും ഉണ്ടോ? അവയ്ക്കു പകരം ഇതുപയോഗിച്ചാല്‍ മതിയോ?
    ഇല്ല, പോരാ. അവയില്‍ പല തരം മുഹൂര്‍ത്തങ്ങള്‍, വ്രതങ്ങള്‍, വിശേഷദിവസങ്ങള്‍ തുടങ്ങിയവയും ചേര്‍ത്തിട്ടുണ്ടു്. കൂടാതെ ഹസ്തരേഖാശാസ്ത്രം, പക്ഷിശാസ്ത്രം, സീതാചക്രം, സുബ്രഹ്മണ്യചക്രം, ദശാചക്രം, ഓരോ നക്ഷത്രത്തിന്റെയും ദേവന്‍, വൃക്ഷം തുടങ്ങിയ വിവരങ്ങള്‍, ഭാവി പ്രവചിക്കാനുള്ള പല വഴികള്‍, വിവാഹപ്പൊരുത്തം തുടങ്ങിയ പല കാര്യങ്ങളുമുണ്ടു്. അവ ഇതിലില്ല.

36. കേരളം: 50 വിശേഷദിവസങ്ങള്‍ എന്നൊരു പരമ്പര എഴുതിവരുകയാണു ഞാന്‍. എഴുതണമെന്നുള്ള പല വിശേഷദിവസങ്ങളും ഇതിലില്ല. അവ ഉള്‍ക്കൊള്ളിക്കാന്‍ എന്താണു വഴി?
    അവയുടെ നിര്‍വ്വചനങ്ങള്‍ (ഉദാ: മീനമാസത്തിലെ അവസാനത്തെ ഭരണിനക്ഷത്രം) അയച്ചുതരുക. ഉള്‍പ്പെടുത്താന്‍ ശ്രമിക്കാം.

37. സീയെസ് ഇവിടെ പറഞ്ഞ പ്രശ്നം പരിഹരിച്ചോ?
    ഇല്ല. ഇതുവരെ അതു നോക്കാന്‍ സമയം കിട്ടിയില്ല.

38. 38 മുതല്‍ 45 വരെയുള്ള പേജുകളിലുള്ള ലഗ്നപ്പട്ടികകളില്‍ ചിലതിന്റെ അവസാനത്തെ കോളത്തിനു് ആവശ്യമില്ലാത്ത വീതിയുണ്ടല്ലോ.
    അതൊരു ബഗ്ഗാണു്. ലാറ്റക് ടേബിള്‍ സെല്ലുകള്‍ക്കു വീതീ നിശ്ചയിക്കുന്നതു് ആ കോളത്തിലെ ഏറ്റവും നീളമുള്ള സ്ട്രിംഗിന്റെ നീളം അനുസരിച്ചാണു്. ഗ്ലിഫ്-ബേസ്ഡ് ആയ ഈ രീതിയില്‍ മലയാളം വാക്കുകളുടെ നീളം ശരിക്കു് ഊഹിക്കാന്‍ വരുന്ന പാകപ്പിഴയാണതു്.

    സെല്ലുകള്‍ക്കു ഫിക്സ്ഡ് വിഡ്ത്ത് കൊടുത്തു് ഇതു പരിഹരിക്കാം. പതുക്കെ ചെയ്യാം.

39. ഇങ്ങനെയുള്ള പ്രവൃത്തികള്‍ വഴി താ‍ങ്കള്‍ പ്രതിലോമചിന്തകള്‍ക്കു വളം വെച്ചു കൊടുക്കുന്നു എന്നല്ലേ ചന്ത്രക്കാറന്‍ ഇവിടെ പറഞ്ഞതു്?
    അതേ. അതു കൊണ്ടു തന്നെയാണു് ഈ അലപ്ര ഇന്നു് ഇവിടെ എഴുതിയതും. ചന്ത്രക്കാറനു നന്ദി.

എതിരവന്‍ കതിരവന്റെ ശിവനടനം-ഏറ്റുമാനൂര്‍ അമ്പലത്തിലെ ചുവര്‍ച്ചിത്രം എന്ന ലേഖനം വളരെ നിലവാരം പുലര്‍ത്തുന്നു. ഏറ്റുമാനൂര്‍ അമ്പലത്തില്‍ പോയാല്‍ ഈ ചിത്രം കാണാന്‍ നന്നേ ബുദ്ധിമുട്ടാണു്. പ്രധാന വാതിലില്‍ക്കൂടി കടന്നാല്‍ വലത്തുവശത്തു് പുറകിലായി ഇതു കാണാം എന്നാണു് എന്റെ ഓര്‍മ്മ.

ഈ ശിവനടനം ഇതേ രീതിയില്‍ രണ്ടു സംസ്കൃതശ്ലോകങ്ങളില്‍ ചിത്രീകൃതമായി കണ്ടിട്ടുണ്ടു്. ഒരെണ്ണം എത്ര ഓര്‍ത്തിട്ടും പുസ്തകങ്ങളില്‍ പരതിയിട്ടും കിട്ടിയില്ല. കിട്ടിയാല്‍ ഇവിടെ ചേര്‍ക്കാം.

മറ്റേ ശ്ലോകം വളരെ പ്രസിദ്ധമാണു്.

വാഗ്ദേവീ ധൃതവല്ലകീ, ശതമഖോ വേണും ദധത്‌, പദ്മജ-
സ്താളോന്നിദ്രകരോ, രമാ ഭഗവതീ ഗേയപ്രയോഗാന്വിതാ,
വിഷ്ണുഃ സാന്ദ്രമൃദങ്ഗവാദനപടുര്‍, ദേവാഃ സമന്താത്‌ സ്ഥിതാഃ
സേവന്തേ തമനു പ്രദോഷസമയേ ദേവം മൃഡാനീപതിം

അര്‍ത്ഥം:

വാഗ്ദേവീ ധൃതവല്ലകീ	:	സരസ്വതീദേവി വീണയേന്തി
ശതമഖഃ വേണും ദധത്	:	ദേവേന്ദ്രന്‍ ഓടക്കുഴലേന്തി
പദ്മജഃ താളോന്നിദ്രകരഃ	:	ബ്രഹ്മാവു് കൈ കൊണ്ടു താളമിട്ടു
ഭഗവതീ രമാ ഗേയ-പ്രയോഗാന്വിതാ	:	ലക്ഷ്മീഭഗവതി പാട്ടു പാടി
വിഷ്ണുഃ സാന്ദ്രമൃദങ്ഗവാദനപടുഃ	:	വിഷ്ണു മൃദംഗം വിദഗ്ദ്ധമായും സാന്ദ്രമായും വായിച്ചു
ദേവാഃ സമന്താത്‌ സ്ഥിതാഃ	:	ദേവന്മാര്‍ ചുറ്റും നിന്നു്
തം മൃഡാനീപതിം ദേവം അനു	:	പാര്‍വ്വതിയുടെ ഭര്‍ത്താവായ ആ ശിവനെത്തന്നെ
പ്രദോഷസമയേ	:	പ്രദോഷസമയത്തു്
സേവന്തേ	:	സേവിക്കുന്നു

(തം + അനു = തമനു. അല്ലാതെ ഊഞ്ഞാലില്‍ക്കയറുന്ന ലവനല്ല.)

---

ഇതു് പ്രദോഷവ്രതമെടുക്കുന്നവര്‍ ചൊല്ലുന്ന ധ്യാനശ്ലോകങ്ങളില്‍ ഒന്നാണു്. “മൃഡാനീപതി” എന്ന പ്രയോഗം ശ്രദ്ധേയം. മൃഡന്റെ ഭാര്യ മൃഡാനി. അപ്പോള്‍ “മൃഡന്റെ ഭാര്യയുടെ ഭര്‍ത്താവു്” എന്നൊരു എടങ്ങേടു പിടിച്ച അര്‍ത്ഥം വരും. “ഭവാനീഭുജംഗം” എന്നു സാക്ഷാല്‍ ശങ്കരാചാര്യര്‍ പ്രയോഗിച്ചിട്ടുണ്ടല്ലോ, പിന്നെന്തു്?

ഉമേഷ് (ഉമേശന്‍) എന്ന പേരിനു് ഇങ്ങനെയൊരു അപകടം ഉണ്ടായേക്കാം എന്നതിനെപ്പറ്റി ഞാനൊരിക്കല്‍ ഇവിടെ പറഞ്ഞിരുന്നു. അയ്യപ്പന്‍ എന്ന സുഹൃത്തിന്റെ കഥയും. വായിക്കാത്തവര്‍ വായിക്കുക. വായിച്ചവര്‍ വീണ്ടും വായിക്കുക.

പരസ്യം കഴിഞ്ഞു. രുക്കാവട് കേ ലിയേ ഖേദ് ഹൈ.

---

ഈ ശ്ലോകം ഒരിക്കല്‍ ഇന്റര്‍നെറ്റ് അക്ഷരശ്ലോകസദസ്സില്‍ (ഇ-സദസ്സ്) രാജേഷ് വര്‍മ്മ ചൊല്ലി. ഇതിനൊരു പരിഭാഷ പെട്ടെന്നു തല്ലിക്കൂട്ടി മറ്റാരെങ്കിലും “വ”യ്ക്കു ശ്ലോകം ചൊല്ലുന്നതിനു മുമ്പു് ഞാന്‍ ചൊല്ലി. ഇ-സദസ്സിലെ ആദ്യത്തെ നിമിഷകവനമായിരുന്നു അതു്.

വീണാവാദിനിയായി വാണി, മഘവാവോടക്കുഴല്‍ക്കാരനായ്‌,
വാണീപന്‍ കരതാളമിട്ടു, രമയോ ഗാനങ്ങളോതീടിനാള്‍,
ഗോവിന്ദന്‍ സുമൃദങ്ഗവാദകനു, മീ മട്ടില്‍ പ്രദോഷത്തിലാ
ദേവന്മാര്‍ പരമേശനെത്തൊഴുതിടാനൊന്നിച്ചു നില്‍പ്പായഹോ!

പെട്ടെന്നു തല്ലിക്കൂട്ടിയതിനാല്‍ തര്‍ജ്ജമ നന്നായിട്ടില്ല. രാജേഷും ഇതിനൊരു പരിഭാഷ തയ്യാറാക്കിയിരുന്നു. അടുപ്പിച്ചു രണ്ടു ശ്ലോകങ്ങള്‍ ഒരാള്‍ക്കു തന്നെ ചൊല്ലാന്‍ പറ്റാത്തതിനാല്‍ ചൊല്ലിയില്ലെന്നേ ഉള്ളൂ. ഇതാണു് ആ ശ്ലോകം.

വീണാപാണിനിയായി വാണി, മുരളീഗാനത്തിനാലിന്ദ്രനും,
താളം കൊട്ടി വിരിഞ്ചനും, മധുരമാം ഗീതത്തിനാല്‍ പൂമകള്‍,
മന്ദ്രം സാന്ദ്രമൃദംഗമോടു ഹരിയും, ചൂഴുന്ന വാനോര്‍കളും,
സേവിക്കുന്നു പ്രദോഷവേളയിലിതാ കാര്‍ത്ത്യായനീകാന്തനെ.

---

നിമിഷപരിഭാഷാകവനങ്ങള്‍ ഇ-സദസ്സില്‍ വേറെയും ഉണ്ടായിട്ടുണ്ടു്. ഒരിക്കല്‍ ജ്യോതിര്‍മയി (വാഗ്‌ജ്യോതി ബ്ലോഗെഴുതുന്ന ജ്യോതിട്ടീച്ചര്‍ തന്നെ)

തമംഗരാ‍ഗം ദദതീം ച കുബ്ജാം
അനംഗബാണാഃ രുരുധുഃ കഥം താം?
കിമംഗ, വാസം ഭവതേ ദദാമി
വിരാഗവര്‍ഷം മയി നിക്ഷിപേസ്ത്വം?

എന്ന ശ്ലോകം എഴുതി അയച്ചപ്പോള്‍ അതിനു പിന്നാലെ ഞാന്‍

കൂനിക്കു, ഗന്ധമിയലും കുറി കൂട്ടവേ, നീ
സൂനാസ്ത്രസായകവിമര്‍ദ്ദിതമാക്കി ചിത്തം;
ഞാനിന്നു വാസമഖിലം തവ നല്‍കിയാലും
നീ നല്‍കിടുന്നതു വിരാഗതയോ മുരാരേ?

എന്ന പരിഭാഷ അയച്ചു. കവയിത്രി ഉദ്ദേശിച്ച അര്‍ത്ഥമൊന്നുമല്ല ഞാന്‍ മനസ്സിലാക്കിയതെന്നു പിന്നീടാണു മനസ്സിലായതു്. അതിനെപ്പറ്റി വിശദമായി ജ്യോതിയുടെ ബ്ലോഗിലെ കുബ്ജാമാധവം എന്ന പോസ്റ്റില്‍ വായിക്കാം.

---

രാജേഷ് വര്‍മ്മയ്ക്കും പറ്റി ഈ അബദ്ധം. ജ്യോതി എഴുതിയ

പ്രവാളപ്രഭാ മഞ്ജു ഭൂഷാന്വിതാംഗീ
രസാസ്വാദതൃഷ്ണാം സമുദ്ദീപയന്തീ
ശരച്ചന്ദ്രികാശീതദാത്രീ ച മേ വാൿ
ഭവേത്‌ സർവദാ നിത്യകാമപ്രദാത്രീ

എന്ന ശ്ലോകത്തെ രാജേഷ്

തളിര്‍ത്തൊത്തിനൊപ്പം മിനു, പ്പമ്പിളിയ്ക്കും
കുളിര്‍ക്കും തണുപ്പൊത്തുലാവുന്ന നിന്‍ മെയ്‌
വിളങ്ങേണമുള്ളില്‍ മൊഴിച്ചേലു നാവില്‍-
ക്കളിയ്ക്കേണമെന്തും കൊടുക്കുന്ന തായേ.

എന്നു ഭുജംഗപ്രയാതത്തില്‍ത്തന്നെ പരിഭാഷപ്പെടുത്തി. (ഇതു് അക്ഷരശ്ലോകക്രമത്തിലായിരുന്നില്ല.) “ആ ശ്ലോകത്തിന്റെ അര്‍ത്ഥം അങ്ങനെയൊന്നുമല്ല” എന്നു ജ്യോതി. അതുകൊണ്ടു രാജേഷ് അതിനെ ഇങ്ങനെ മാറ്റി.

തളിര്‍ത്തൊത്തിനൊപ്പം മിനു, പ്പുള്ളു കാണാന്‍
മുളയ്ക്കുന്നൊരാക്കം പെരുക്കുന്ന ചന്തം,
വളര്‍തിങ്കളെപ്പോല്‍ത്തണു,പ്പെന്നിതെല്ലാം
വിളങ്ങും മൊഴിച്ചേലു നാവില്‍ക്കളിയ്ക്ക.

ഈ കഥ രാജേഷ് ആശ കൊണ്ടു്… എന്ന പോസ്റ്റില്‍ എഴുതിയിട്ടുണ്ടു്.

---

“പരിഭാഷായന്ത്രം” എന്നു പില്‍ക്കാലത്തു സന്തോഷ് വിശേഷിപ്പിച്ച രാജേഷിന്റെ മറ്റൊരു തര്‍ജ്ജമ.

മൂലശ്ലോകം എഴുതിയതു് ജ്യോതിയുടെ ഏട്ടന്‍ പി. സി. മധുരാജ് ആണു്.

യദി ഹൃത്കമലേ മധുപാനരതോ
വരദോ മുരളീധര ഭൃങ്ഗവരഃ
സുമഗന്ധ സുഭക്തിരസേ സരസഃ
ക്വ സഖേ തരുണീ കബരീ വിപിനം?

പ്രസിദ്ധമായ

ഉഡുരാജമുഖീ മൃഗരാജകടീ
ഗജരാജ വിരാജിത മന്ദഗതീ
യദി സാ യുവതീ ഹൃദയേ വസതീ
ക്വ ജപഃ? ക്വ തപഃ? ക്വ സമാധി വിധി?

എന്ന സരസശ്ലോകത്തിനു പിന്നാലെ ചൊല്ലാന്‍ വേണ്ടി മധുരാജ് എഴുതിയ ശ്ലോകമാണിതു്. രാജേഷിന്റെ തോടകവൃത്തത്തില്‍ത്തന്നെയുള്ള മലയാളപരിഭാഷ:

ശമമാം സുമഗന്ധമുതിര്‍ന്നിടുമെന്‍
ഹൃദയത്തിലെ ഭക്തിരസം നുകരാന്‍
സരസന്‍ ഹരിയാമളിയെത്തിടുകില്‍
തരുണീ കബരീ വനമെന്തിവന്‌?

അക്ഷരശ്ലോകസദസ്സിലെ അനുഗൃഹീതകവിയായ ബാലേന്ദുവും ഇതുപോലെ പല നിമിഷപരിഭാഷകളും ചെയ്തിട്ടുണ്ടു്. ഒന്നും ഓര്‍മ്മ കിട്ടുന്നില്ല. കിട്ടുന്നതിനനുസരിച്ചു് ഇവിടെച്ചേര്‍ക്കാം.

---

ഇന്റര്‍നെറ്റിലെ അക്ഷരശ്ലോകസദസ്സിനെപ്പറ്റി കൂടുതല്‍ വിവരങ്ങള്‍ ഇവിടെ കാണാം. ഈ ശ്ലോകങ്ങളെല്ലാം അവിടെയുണ്ടു്.

2006 മാര്‍ച്ചു മുതല്‍ 2007 നവംബര്‍ വരെ തുടങ്ങിവെച്ച മുപ്പത്തിയെട്ടു പോസ്റ്റുകളാണു ഡ്രാഫ്റ്റ് രൂപത്തില്‍ ഗുരുകുലത്തില്‍ കിടക്കുന്നതു്. ആരംഭശൂരത്വം കൊണ്ടും പൂര്‍ണ്ണതാവ്യഗ്രത കൊണ്ടും തീര്‍ക്കാതെ കിടക്കുന്നവയാണു ഭൂരിപക്ഷവും. വിഷയത്തിലുള്ള താത്പര്യമോ അതിന്റെ പ്രസക്തിയോ നഷ്ടപ്പെട്ടവയുമുണ്ടു കുറെയെണ്ണം. ഇനി മുതല്‍ പുതിയ പോസ്റ്റുകള്‍ എഴുതുന്നതിനു പകരം ഡ്രാഫ്റ്റന്മാരെ മുഴുമിക്കാന്‍ ശ്രമിക്കണം എന്നു കരുതിയതിന്റെ ഫലമാണു് കഴിഞ്ഞ രണ്ടു പോസ്റ്റുകള്‍.

പ്രോത്സാഹനം എഴുതിത്തുടങ്ങിയതു 2007 ജൂലായില്‍ ആണു്. ശ്ലോകവും അര്‍ത്ഥവുമെഴുതി ഇട്ടിരുന്നു. വിശദീകരണമായി കമന്റുകള്‍ എങ്ങനെ ബ്ലോഗുകളെ നല്ല രീതിയില്‍ ബാധിക്കുന്നു, പോസ്റ്റ്/കമന്റ് അഗ്രിഗേറ്ററുകളെപ്പറ്റിയും വായനലിസ്റ്റിനെപ്പറ്റിയും എനിക്കുള്ള അഭിപ്രായങ്ങള്‍ തുടങ്ങിയവ ഉള്‍പ്പെടുന്ന ഒരു കനത്ത ലേഖനം എഴുതിത്തുടങ്ങിയതുമാണു്. അതു് ഇപ്പോഴെങ്ങും തീരില്ല എന്നു തോന്നിയപ്പോള്‍ എടുത്തുകളഞ്ഞിട്ടു് അപ്പോള്‍ തോന്നിയതാണു് ജ്ഞാനപ്പാനയുടെ പാരഡി എഴുതാന്‍. ബുദ്ധിരാക്ഷസനായ വക്കാരി അതു് എങ്ങനെയോ മണത്തറിഞ്ഞു ഈ കമന്റിലൂടെ!

അബദ്ധധാരണകള്‍ അതിനും മുമ്പു തുടങ്ങിയതാണു്. “എന്റെ ഓര്‍മ്മയില്‍ ഞാന്‍ ആദ്യമായി വായിക്കുന്ന…” എന്ന ഖണ്ഡിക തൊട്ടായിരുന്നു ആ പോസ്റ്റ്. രാം മോഹന്റെ അന്നങ്ങള്‍ പോയ വഴി ആണു് അതു മുഴുമിക്കാന്‍ പിന്നെയും പ്രചോദനം തന്നതു്. അഞ്ചു ദിവസം മുമ്പു് അതു പ്രസിദ്ധീകരിക്കാന്‍ വേണ്ടി അതിനു മുമ്പു് ഒരു ചെറിയ ഉപക്രമം എഴുതാന്‍ ശ്രമിച്ചതാണു് അമ്മാവന്റെയും ചിറ്റപ്പന്റെയും കഥ പറഞ്ഞു വൃഥാസ്ഥൂലമായതു്. പതിവുള്ള എഡിറ്റിംഗ് ചെയ്യാന്‍ ക്ഷമയുണ്ടായില്ല.

അതിലും വലിയ പ്രശ്നം ഉണ്ടായതു് അതില്‍ എഴുതാന്‍ ഉദ്ദേശിച്ചിരുന്ന പല കാര്യങ്ങളും പോസ്റ്റു ചെയ്തപ്പോള്‍ വിട്ടുപോയി എന്നതാണു്. അവയില്‍ ചിലതൊക്കെ പെറുക്കിക്കൂട്ടി നിരത്തിയിരിക്കുകയാണു് ഈ പോസ്റ്റില്‍. പുതിയ പോസ്റ്റ് ഉടനെയെങ്ങും എഴുതില്ല എന്ന തീരുമാനത്തിന്റെ ആദ്യത്തെ ലംഘനം.

---

ഞാന്‍ വായിച്ചു തുടങ്ങിയ കാലത്തു് ഇന്നത്തെപ്പോലെ കുട്ടികള്‍ക്കുള്ള പ്രസിദ്ധീകരണങ്ങള്‍ കാര്യമായി ഉണ്ടായിരുന്നില്ല. ജനയുഗത്തിന്റെ ബാലപ്രസിദ്ധീകരണമായ “ബാലയുഗം” മാത്രമായിരുന്നു ശരണം. വല്ലപ്പോഴും സ്കൂളില്‍ നിന്നു “തളിരു്” എന്ന സാധനവും കിട്ടും. ബാക്കി വായനയൊക്കെ മുതിര്‍ന്നവരുടെ പുസ്തകങ്ങള്‍ തന്നെ. (ഇങ്ങനെ “മാതൃഭൂമി” ആഴ്ചപ്പതിപ്പു വായിച്ചതു കൊണ്ടുണ്ടായ ഒരു അപകടത്തെപ്പറ്റി ഇവിടെ പറയുന്നുണ്ടു്.)

ഏഴെട്ടു വയസ്സുള്ളപ്പോള്‍ ആദ്യമായി വായിക്കുന്ന പുസ്തകങ്ങളില്‍ പൊന്‍‌കുന്നം ദാമോദരന്റെ രാക്കിളികള്‍ (കര്‍ഷകത്തൊഴിലാളികളായ നാണുവും പവാനിയും തമ്മില്‍ കണ്ടുമുട്ടുന്നതും പവാനി ഗര്‍ഭിണിയാകുന്നതും പിന്നെ അവര്‍ കല്യാണം കഴിക്കുന്നതും അതിനു ശേഷം പവാനി വീണ്ടും വീണ്ടും ഗര്‍ഭിണിയാകുന്നതും കുഞ്ഞുങ്ങളെ നോക്കാന്‍ കഴിയാതെ അവര്‍ കഷ്ടപ്പെടുന്നതും അവസാനം പവാനി പ്രസവിച്ചു കിടക്കുന്ന ആശുപത്രിയുടെ വെളിയിലുള്ള സര്‍വ്വേക്കല്ലില്‍ നാണു തല തല്ലി ചാവുന്നതും ആണു കഥാതന്തു. കുടുംബാസൂത്രണപ്രചാരണത്തിനായി എഴുതിയ ഒരു നോവല്‍.), കാട്ടാക്കട ദിവാകരന്റെ കിളിക്കൂടു് (അമ്മാവന്റെ മകളായ ശ്രീദേവിയെ ചതിച്ചിട്ടു പട്ടണത്തില്‍ പോയി വലിയ ഡോക്ടറായ രവിയുടെ ഭാര്യയുടെ അച്ഛന്റെ രണ്ടാം ഭാര്യയായി ശ്രീദേവി എത്തുന്നതും അതിനു ശേഷമുള്ള ഉദ്വേഗജനകങ്ങളായ സംഭവവികാസങ്ങളുമാണു് ഇതിന്റെ ഇതിവൃത്തം. ചതിച്ചിട്ടു പോയ മുന്‍‌കാമുകന്റെ ശല്യം സഹിക്കാന്‍ വയ്യാതെ ആത്മഹത്യ ചെയ്ത സരോജിനി എന്നൊരു ചേച്ചിയും, അവളുടെ മുന്‍‌കാമുകനെ കുത്തിമലര്‍ത്തിയിട്ടു നാടുവിട്ടുപോയ രഘു എന്നൊരു ചേട്ടനും ശ്രീദേവിക്കുണ്ടു്. രഘു നാടു വിട്ടു പോയിട്ടു് ഏതാനും മാസങ്ങള്‍ക്കു ശേഷം കുറച്ചകലെ താമസിക്കുന്ന ആശാന്റെ മകള്‍ പങ്കലാച്ചി ശ്രീദേവിയുടെ വീട്ടിലെത്തി രഘുവിന്റെ കുഞ്ഞിനെ അവിടെ പ്രസവിക്കുകയുണ്ടായി.) തുടങ്ങിയ മഹത്തായ ആഖ്യായികകള്‍ ഉള്‍പ്പെടുന്നു. ഇവയിലെ ദ്വയാര്‍ത്ഥപ്രയോഗങ്ങളുള്‍പ്പെടെ മനസ്സിലാകാത്ത ഒരുപാടു കാര്യങ്ങളുണ്ടായിരുന്നു. പലതിനും മുമ്പു പറഞ്ഞ അതീന്ദ്രിയദ്ധ്യാനം വഴി സമ്പാദിച്ച അര്‍ത്ഥങ്ങള്‍ മനസ്സിലാക്കുകയും ഭാവിയില്‍ അതൊക്കെ അബദ്ധമാണെന്നു മനസ്സിലാക്കുകയും ചെയ്തു.

ആയിടെ തന്നെ കെ. സുരേന്ദ്രന്റെ “മരണം ദുര്‍ബ്ബലം” എന്ന നോവല്‍ വായിക്കാന്‍ തുടങ്ങുകയും അതില്‍ മായമ്മ എന്നോ മറ്റോ പറയുന്ന നായികയും ഒരു കവിയും തമ്മിലുള്ള വക്കാരിയുടെ കമന്റുകള്‍ മാതിരിയുള്ള നെടുങ്കന്‍ കത്തുകള്‍ വായിച്ചു് അന്തം വിട്ടു കുന്തം വിഴുങ്ങി വായന നിര്‍ത്തുകയും ചെയ്തു. പിന്നെ കുറെക്കാലം കഴിഞ്ഞു “ജ്വാല” വായിക്കുന്നതു വരെ കെ. സുരേന്ദ്രന്‍ എന്നു കേള്‍ക്കുന്നതു തന്നെ പേടിയായിരുന്നു.

---

എന്റെ വായനശീലം വര്‍ദ്ധിപ്പിക്കാന്‍ ഗണ്യമായ ഒരു പങ്കു വഹിച്ചതു ലോറികളും ബസ്സുകളുമായിരുന്നു.

ലോറികളുടെ പിറകില്‍ മലയാളത്തിലും ഇംഗ്ലീഷിലും ആപ്തവാക്യങ്ങള്‍ ഉണ്ടാവും. “ദൈവമേ”, “പിന്നെക്കാണാം” തുടങ്ങിയ ഒറ്റവാക്‍സന്ദേശങ്ങള്‍ തൊട്ടു് “എനിക്കു വിശക്കുന്നു”, “നാം രണ്ടു്, നമുക്കു രണ്ടു്”, “എനിക്കു നീയും നിനക്കു ഞാനും” തുടങ്ങിയ മഹദ്വചനങ്ങള്‍ വരെ അവിടെ കാണാം. വര്‍ഷങ്ങള്‍ക്കു ശേഷം അമേരിക്കയിലെ കാറുകളിലെ ആലോചനാമൃതമായ ബമ്പര്‍ സ്റ്റിക്കറുകള്‍ കാണുമ്പോള്‍ (ഉദാ: ബുഷിനെതിരായ ഒരു ബമ്പര്‍ സ്റ്റിക്കര്‍: “No one died when Clinton lied!”) ഞാന്‍ ഈ ലോറിസന്ദേശങ്ങള്‍ ഓര്‍ക്കാറുണ്ടു്.

ബസ്സിനകത്തും (പ്രൈവറ്റ് ബസ്സുകള്‍) ഇങ്ങനെ പല സന്ദേശങ്ങളുണ്ടു്. “കയ്യും തലയും പുറത്തിടരുതു്”, “പുകവലി പാടില്ല” (സാധാരണ ഇതിലെ “പുലി” ആരെങ്കിലും മായ്ച്ചു കളഞ്ഞിട്ടുണ്ടാവും.), “എന്നെ തൊടരുതു്”, “എന്നെ ചവിട്ടരുതു്” തുടങ്ങിയവ. (അവസാനത്തെ രണ്ടെണ്ണം ഡ്രൈവറുടെ ഇടത്തുവശത്തുള്ള തൊട്ടാല്‍ ചുട്ടുപൊള്ളുന്ന പെട്ടിയുടെ പുറത്തുള്ളതാണു്. അതിനു മുകളില്‍ എപ്പോഴും വിറച്ചുകൊണ്ടിരിക്കുന്ന ഒരു കോലുമുണ്ടു്. ബോറടിക്കുമ്പോള്‍ ഡ്രൈവര്‍ ഇടയ്ക്കിടെ അതു് അങ്ങോട്ടും ഇങ്ങോട്ടും തട്ടുന്നതു കാണാം. അതിന്റെയൊന്നും പേരൊന്നും ആരോടും ചോദിച്ചിട്ടില്ല. ആ പെട്ടിയുടെയും ഇടത്തു വശത്തായി ഒരു തടിപ്പെട്ടിയുണ്ടു്. അതായിരുന്നു എന്റെ ഫേവറിറ്റ് സീറ്റ്. അവിടെയിരുന്നാല്‍ ഡ്രൈവര്‍ ചെയ്യുന്നതു കമ്പ്ലീറ്റ് കാണാം. ഇടയ്ക്കിടെ എഴുനേറ്റു കൊടുക്കേണ്ടിവരും. വണ്ടിയ്ക്കാവശ്യമുള്ള സ്പാനര്‍, കൈ തുടയ്ക്കുന്ന തോര്‍ത്തു്, ചീപ്പു്, കണ്ണാടി, മുറുക്കാന്‍ ചെല്ലം തുടങ്ങിയവ അതിനകത്താണു വെച്ചിരിക്കുന്നതു്.) കൂടാതെ ബസ്സിന്റെ മുന്‍ഭാഗത്തു യേശുക്രിസ്തുവിന്റെ ഒരു പടവും (ഇതെന്താ ക്രിസ്ത്യാനികള്‍ക്കു മാത്രമേ ബസ്സുള്ളോ? അതോ ബസ് ട്രാന്‍സ്പോര്‍ട്ടേഷന്‍ വകുപ്പു ദൈവമാണോ ക്രിസ്തു?) കൂടെ ഒരു ബൈബിള്‍ വചനവും ഉണ്ടാവും. ഇവയില്‍ ചിലവയാണു് എന്റെ വായനതൃഷ്ണയെ വിജൃംഭിച്ചതു്.

---

ആദ്യത്തെ വേദവാക്യം

യഹോവ എന്റെ ഇടയനാകുന്നു, എനിക്കു മുട്ടുണ്ടാവുകയില്ല

എന്നതായിരുന്നു. യഹോവ ഇടയനായാല്‍ മുട്ടിനു് എന്തു സംഭവിക്കും എന്നു് എത്ര ആലോചിച്ചിട്ടും മനസ്സിലായില്ല. “ഇവിടെ കുറേ അഹങ്കാരികള്‍ ക്രിസ്ത്യാനികള്‍ ഉണ്ടു്. എല്ലാറ്റിന്റെയും മുട്ടു തല്ലിയൊടിക്കണം” എന്നു ചില ഹിന്ദുത്വതീവ്രവാദികള്‍ പറയുന്നതു കേട്ടിട്ടുണ്ടു്. യഹോവയെ പിന്തുടര്‍ന്നാല്‍ ആരെങ്കിലും മുട്ടു തല്ലിയൊടിക്കും എന്നു യഹോവയോടു പരാതി പറയുകയാണു് എന്നാണു് ആദ്യം കരുതിയതു്. മുട്ടിന്റെ ഇവിടെ ഉദ്ദേശിച്ച അര്‍ത്ഥം പിന്നീടാണു മനസ്സിലായതു്. The Lord is my shepherd. I have everything I need. (Psalms 23:1)

---

“മുട്ടു്” എന്ന വാക്കിന്റെ അര്‍ത്ഥം മനസ്സിലാകാത്തതു കൊണ്ടാണു് മുകളില്‍ പറഞ്ഞതു മനസ്സിലാവാത്തതെങ്കില്‍, “ദൂരാന്വയം” എന്ന കാവ്യദോഷമാണു് താഴെപ്പറയുന്ന വാക്യത്തെ ദുര്‍ഗ്രഹമാക്കിയതു്.

നിന്റെ കൃപ എനിക്കു മതി.

ഇതിലെ നാലു വാക്കുകളും നന്നായി അറിയാം. പക്ഷേ ഈ വാക്യത്തിന്റെ അര്‍ത്ഥം മനസ്സിലാക്കാന്‍ ഒരുപാടു കാലമെടുത്തു.

ആദ്യം തോന്നിയ അര്‍ത്ഥം ഇതാണു്: “ദൈവമേ, കുറെക്കാലമായി നീ എനിക്കു കൃപ തരുന്നു. ഇഷ്ടം പോലെ കിട്ടി. ഇനി എനിക്കു മതി. മടുത്തു. അതിനാല്‍, പ്ലീസ്, നീ എനിക്കു കൃപ തരരുതു്.”

ഇതിനൊരു പന്തികേടു്. കൃപ തരരുതു് എന്നു് ആരെങ്കിലും പ്രാര്‍ത്ഥിക്കുമോ? അതോ ദൈവം പരമകാരുണികനാണു് എന്നു് ഊന്നിപ്പറയുകയാണോ ഇതു്?

കുറച്ചു കഴിഞ്ഞപ്പോള്‍ തോന്നിയതു് ഇതാണു്: “നിന്റെ കൃപ എനിക്കു തന്നാല്‍ മതി. ഈ നാട്ടിലുള്ള വേറേ ഒരൊറ്റ അലവലാതിയ്ക്കും കൊടുത്തു പോകരുതു്.”

സുവിശേഷകര്‍ ഫ്രീയായി തരുന്ന ചുവന്ന പുറംചട്ടയും പോക്കറ്റിലിടാന്‍ തക്കവണ്ണം ചെറുപ്പവും മിനുസമുള്ള കടലാസും ചെറിയ അക്ഷരങ്ങളും ഉള്ള ഇംഗ്ലീഷ് ബൈബിളില്‍…

ഇതിലാണു ഞാന്‍ ആദ്യമായി internationalization കാണുന്നതു്. യോഹന്നാന്റെ സുവിശേഷം മൂന്നാം അദ്ധ്യായം പതിനാറാം വാക്യം അതിന്റെ ആദിയില്‍ പല ലോകഭാഷകളിലും എഴുതിയിരുന്നു. ഇന്ത്യന്‍ ഭാഷകളില്‍ ഹിന്ദിയും (क्योंकि परमेश्वर ने …) തമിഴും (தேவன், …) മാത്രമേ ഉണ്ടായിരുന്നുള്ളൂ. അതില്‍ മലയാളം ഇല്ലാത്തതില്‍ ഞാന്‍ ആരോടൊക്കെയോ രോഷം കൊണ്ടിരുന്നു. ഇന്നും അതു തുടരുന്നു. യൂണിക്കോഡിലും ഗൂഗിളിലും മറ്റും ഇല്ലാത്തതിനാണെന്നു മാത്രം.

…ഇതിന്റെ ഇംഗ്ലീഷ് രൂപം (My grace is all you need. 2 Cor. 12:9) വര്‍ഷങ്ങള്‍ക്കു ശേഷം കണ്ടപ്പോഴാണു് ഇതിന്റെ വിവക്ഷ “എനിക്കു നിന്റെ കൃപ മതി, വേറേ ഒരു കുന്തവും വേണ്ടാ” എന്നാണെന്നു മനസ്സിലായതു്. മലയാളമറിയാത്ത പാതിരിമാര്‍ തോന്നിയതു പോലെ പരിഭാഷപ്പെടുത്തിയ ബൈബിള്‍ പില്‍ക്കാലത്തെങ്കിലും അല്പം കൂടി നല്ല ഭാഷയില്‍ കണ്ടു വരുന്നു എന്നതു് ആശ്വാസജനകമാണു്.

(ഇതെഴുതിക്കഴിഞ്ഞു റെഫറന്‍സ് തപ്പിയപ്പോഴാണു കൊറിന്ത്യരുടെ രണ്ടാം ലേഖനം ഇരുപത്താറാം അദ്ധ്യായം ഒമ്പതാം വാക്യത്തില്‍ “എന്റെ കൃപ നിനക്കു മതി” എന്നാണെന്നു കണ്ടതു്. ഏതായാലും അബദ്ധധാരണകളെപ്പറ്റിയുള്ള ലേഖനമായതു കൊണ്ടു് അതു തിരുത്തുന്നില്ല. ഒട്ടാവ/ഒഷാവ പോലെ ഞാന്‍ ഇതു പലരോടും പറഞ്ഞിട്ടുണ്ടു്. അതു കേട്ട ആരെങ്കിലും ബൈബിളില്‍ ആ വാക്യവും ചേര്‍ത്തിരിക്കാന്‍ സാദ്ധ്യതയുണ്ടു്. :))

ഇനി, “നിന്റെ കൃപ എനിക്കു മതി” എന്ന വാക്യം ബൈബിളില്‍ എവിടെയെങ്കിലും കണ്ടാല്‍ ദയവായി എന്നെ അറിയിക്കുക. പ്ലൂട്ടോയുടെ കാര്യത്തിലെന്നതു പോലെ ഇവിടെയും എനിക്കൊന്നു് ഊരിയെടുക്കാമല്ലോ :))

---

ഇതിലെ ബൈബിള്‍ വാക്യങ്ങളുടെ റെഫറന്‍സ് കണ്ടെടുത്തു തന്ന കുട്ട്യേടത്തി, ഇഞ്ചിപ്പെണ്ണു്, സിബു, തമനു എന്നിവര്‍ക്കു നന്ദി.

(ഇവരില്‍ തമനു ഒരു കുന്തവും ചെയ്തിട്ടില്ല. അവനു കൂദാശ എത്രയുണ്ടെന്നു പോലും അറിയില്ല. നാട്ടുകാരനല്ലേ, ചേതമില്ലാത്ത ഒരുപകാരമിരിക്കട്ടേ എന്നു കരുതി :))

---

ഞാന്‍ ആദ്യമായി ചെസ്സുകളി കണ്ടതു് തൊട്ടടുത്തുള്ള പഞ്ചായത്ത് ഗ്രൌണ്ടില്‍ വോളിബോള്‍ കളി കാണാന്‍ പോകുമ്പോഴാണു്.

മുതിര്‍ന്നവരുടെ കളിയാണു്. പന്തു വരാന്‍ സാദ്ധ്യതയുള്ള സ്ഥലത്തു നില്‍ക്കുന്നതു തന്നെ അപകടമാണു്. പിന്നല്ലേ കളിക്കുന്നതു്! എങ്കിലും റഫറിയായി നടിച്ചു് ഒരു പോസ്റ്റിന്റെ മുകളില്‍ കയറി നില്‍ക്കുക, സ്കോര്‍ കീപ്പിംഗ് നടത്തുക, വെളിയില്‍ പോകുന്ന പന്തെടുത്തു കൊടുക്കുക, “അടി…”, “ഇടി…”, കൊടു്…”, “ശ്ശേ…”, “കലക്കി…”, “അതു മതി…” തുടങ്ങിയ വ്യാക്ഷേപകങ്ങള്‍ പുറപ്പെടുവിക്കുക, ടച്ചൂണ്ടോ, ക്രോസ് ചെയ്തോ, പന്തു് ഔട്ടാണോ റൈറ്റാണോ തുടങ്ങിയ തര്‍ക്കങ്ങള്‍ വരുമ്പോള്‍ വിലയേറിയ അഭിപ്രായങ്ങള്‍ (ആരും വിലമതിക്കില്ലെങ്കിലും) പ്രകടിപ്പിക്കുക ഇത്യാദി എണ്ണമറ്റ സേവനങ്ങള്‍ ചെയ്തുപോന്നു.

ചില ദിവസം സര്‍ക്കാര്‍ ജോലിക്കാ‍രായ രണ്ടുപേര്‍ ഒരു ചെസ്സ് സെറ്റുമായി വരും. അവിടെ പന്തുകളി നടക്കുമ്പോള്‍ ഇവിടെ ചെസ്സുകളി നടക്കും. ഇവര്‍ വരുന്ന ദിവസങ്ങളില്‍ ഞാന്‍ പന്തുകളി വിട്ടിട്ടു് ചെസ്സുകളി കാണാന്‍ പോയി ഇരിക്കും. പഴം കളി, ഇരുപത്തിനാലു നായും പുലിയും, പാറ കൊത്തു് (കൊത്തുകല്ലു്) തുടങ്ങിയ ഇന്‍ഡോര്‍ ഗെയിമുകളില്‍ നിഷ്ണാതനായിരുന്നെങ്കിലും ഈ സാധനം കാര്യമായി മനസ്സിലായിരുന്നില്ല. ഏറ്റവും ബുദ്ധിമുട്ടു് കാലാളിന്റെ നീക്കമായിരുന്നു. ചിലപ്പോള്‍ ഒരു കളം, ചിലപ്പോള്‍ രണ്ടു കളം, ചിലപ്പോള്‍ കോണോടു കോണായി… ആകെ കണ്‍ഫ്യൂഷന്‍! ചോദിക്കുന്നതെങ്ങനെ? എനിക്കീ കളി അറിയില്ല എന്നു് അവര്‍ അറിയില്ലേ? അതുകൊണ്ടു് കളിയെല്ല്ലാം മനസ്സിലായി എന്നു നടിച്ചു തലയാട്ടി ഞാന്‍ അവിടെയിരിക്കും.

കുറെക്കാലം അങ്ങനെയിരുന്നപ്പോള്‍ നീക്കങ്ങളൊക്കെ പഠിച്ചു. എപ്പോഴാണു കളി തീരുന്നതു് എന്നു മാത്രം മനസ്സിലായില്ല. എനിക്കറിയാവുന്ന മറ്റു കളികളിലൊക്കെ ഒരാളുടെ കരുക്കളെല്ലാം തീരുമ്പോഴാണു കളി തീരുന്നതു്. ഇതില്‍ ഇടയ്ക്കു് ധാരാളം കരുക്കള്‍ ബാക്കിയിരിക്കുമ്പോള്‍ത്തന്നെ “കലക്കന്‍ കളിയായിരുന്നു” എന്നും മറ്റും പറഞ്ഞു നിര്‍ത്തുന്നതു കാണാം. ചോദിക്കാന്‍ പറ്റുമോ? അതിന്റെ ജീന്‍ വേണ്ടേ?

അങ്ങനെയിരിക്കേ ഒരു ദിവസം ഒരാള്‍ വിചിത്രമായ ഒരു നീക്കം നടത്തി. രാജാവിനെയും തേരിനെയും ഒരു നീക്കത്തില്‍ത്തന്നെ അങ്ങോട്ടുമിങ്ങോട്ടും നീക്കുന്ന വിദ്യ. “അതെന്താ?” എന്ന എന്റെ ചോദ്യം ജീനില്ലാത്തതു കൊണ്ടു തൊണ്ടയില്‍ത്തന്നെ കുരുങ്ങി. അപ്പോള്‍ നീക്കം നടത്തിയ ആളിന്റെ എതിരാളി ചോദിച്ചു.

“അതെന്താ?”

സമാധാനം. ഞാന്‍ ചെവി കൂര്‍പ്പിച്ചിരുന്നു.

“ഓ അതോ, അതു ഡയസ് നോണ്‍”

അവര്‍ എന്തോ ജോലിക്കാര്യം സംസാരിച്ചു കൊണ്ടിരുന്നതിന്റെ തുടര്‍ച്ചയാണു് അതെന്നു് എനിക്കു മനസ്സിലായില്ല. ആ നീക്കത്തിന്റെ പേരാണെന്നാണു ഞാന്‍ കരുതിയതു്.

ഏതാനും ദിവസം കഴിഞ്ഞപ്പോള്‍ “ഡയസ് നോണ്‍” എങ്ങനെ നീക്കും എന്നെനിക്കു മനസ്സിലായി. രാജാവിനെ അതേ നിറത്തിലുള്ള തൊട്ടടുത്ത കളത്തിലേക്കു നീക്കുക. അതു ചാടിക്കടന്ന കളത്തിലേക്കു തേരിനെ വെയ്ക്കുക. അവയ്ക്കിടയില്‍ കരുക്കളുണ്ടെങ്കില്‍ ചെയ്യാന്‍ പാടില്ല എന്നു തോന്നുന്നു.

കാലം കുറേക്കഴിഞ്ഞു. ഇപ്പോള്‍ അത്യാവശ്യമായി അടിയറവും മറ്റും മനസ്സിലായി. കുറേശ്ശെ കളിച്ചും തുടങ്ങി, ജയിക്കാറില്ലെങ്കിലും.

എന്റെ വീടിനടുത്തു് ആകെ ഒരു സ്ഥലത്തേ ചെസ്സ് സെറ്റൂള്ളൂ. വൈ. എം. ഏ. ലൈബ്രറിയില്‍. രണ്ടു പേര്‍ കളിക്കുന്നുണ്ടാവും. പത്തിരുപതു പേര്‍ ചുറ്റും നിന്നു് “അതു കളി”, “ഇതു കളി”, “ഇവനെന്താ ഈ ചെയ്യുന്നതു്”, “മന്ത്രിയെക്കാള്‍ സ്ട്രോംഗ് കുതിരയല്ലേ” എന്നും മറ്റും ബഹളമുണ്ടാക്കിക്കൊണ്ടിരിക്കും. ഈ ബഹളക്കൂട്ടത്തില്‍ ഞാനും ഒരു സജീവാംഗമായിരുന്നു.

ഒരിക്കല്‍ നടുക്കിരിക്കുന്ന രാജാവിനെതിരേ ആക്രമണം കൊടുമ്പിരിക്കൊള്ളുന്ന സമയത്തു് അക്രമത്തിനിരയാകുന്നവനെ സഹായിച്ചുകൊണ്ടു ഞാന്‍ ഗര്‍ജ്ജിച്ചു:

“ഡയസ് നോണ്‍ ചെയ്യു്”

ലൈബ്രറിയിലുണ്ടായിരുന്ന എല്ലാവരുടെയും കണ്ണുകള്‍ ഒരുമിച്ചു് എന്റെ മേല്‍ പതിച്ചു.

“ഡയസ് നോണ്‍” എന്നു വെച്ചാല്‍ ജോലി ചെയ്യാതെ സമരമോ മറ്റോ ചെയ്താല്‍ ശമ്പളം പിടിക്കുകയോ മറ്റോ ചെയ്യുന്ന സര്‍ക്കാര്‍ ജോലി ജാര്‍ഗണാണെന്നും ചെസ്സിലെ നീക്കത്തിന്റെ പേരു് “കാസ്ലിംഗ്” (Castling) എന്നാണെന്നും അന്നു ഞാന്‍ മനസ്സിലാക്കി.

പിന്നീടു് എത്രയോ തവണ O-O എന്നും O-O-O എന്നും സ്കോര്‍ ഷീറ്റില്‍ എഴുതി ഞാന്‍ കാസ്ലിംഗ് ചെയ്തിരിക്കുന്നു. ഓരോ തവണയും ഞാന്‍ ഡയസ് നോണിനെ ഓര്‍ക്കും.

എന്‍-പാസന്റ് എന്ന വിദ്യ അവര്‍ക്കറിയില്ലായിരുന്നു എന്നു തോന്നുന്നു. അറിയാമായിരുന്നെങ്കില്‍ ഞാന്‍ അതിനെ “കമ്യൂട്ടഡ് ലീവ്” എന്നോ മറ്റോ വിളിച്ചേനേ.

---

ആദ്യമായി കടലാസ്സില്‍ നോക്കി ഒരു ചെസ്സ് ഗെയിം കളിച്ചു നോക്കിയതു് 1978-ല്‍ കാര്‍പ്പോവും കൊര്‍ച്ച്നോയിയും ലോക ചാമ്പ്യന്‍ ഷിപ്പു കളിച്ചപ്പോഴാണു്. Sports in the USSR എന്ന മാ‍സികയില്‍ കാര്‍പ്പോവ് ജയിച്ച ആറു കളികളും ഉണ്ടായിരുന്നു. അതു കളിച്ചു നോക്കിയിട്ടു് കാര്യമായി ഒന്നും മനസ്സിലായില്ല. 1. c4 e6 2. Nc3 d5 3. d4 എന്നീ നീക്കങ്ങള്‍ക്കു ശേഷം (അതില്‍ descriptive notation-ല്‍ ആയിരുന്നു. 1. P-QB4 P-K3 2. N-QB3 P-Q4 3. P-Q4) c4-ലെ കാലാളിനെ അഞ്ചാറു നീക്കങ്ങള്‍ കഴിയുന്നതു വരെ കാര്‍പ്പോവ് വെട്ടാത്തതെന്താണെന്നു തല പുകഞ്ഞാലോചിച്ചു മണിക്കൂറുകള്‍ കളഞ്ഞിട്ടുണ്ടു്. മൂര്‍ത്തി പറഞ്ഞ എതിരന്‍ പുസ്തകങ്ങള്‍ പോയിട്ടു് ടി. കെ. ജോസഫ് തറപ്പേലിന്റെ “ചെസ്സ് മാസ്റ്റര്‍” എന്ന മലയാളപുസ്തകം പോലും ഉണ്ടെന്നു് അറിയാത്ത കാലം. ആറുകളിയും തോറ്റ കോര്‍ച്ച്നോയി ഒരു മണ്ടന്‍ കളിക്കാരനായിരുന്നു എന്നായിരുന്നു എന്റെ വിചാരം.

ആദ്യത്തെ ചെസ്സ് പുസ്തകം പ്രഭാത് ബുക്ക് ഹൌസിന്റെ ചലിക്കുന്ന പുസ്തകശാലയില്‍ നിന്നു വാങ്ങിയ “Your first move” (സൊക്കോള്‍സ്കി എഴുതിയതു്) ആയിരുന്നു. അതില്‍ കോര്‍ച്ച്നോയിയെപ്പോലെ മറ്റൊരു മണ്ടനെ കണ്ടുമുട്ടി. ഇദ്ദേഹം എല്ലാ കളികളിലും തോറ്റിരുന്നു. Amateur എന്നാണു പേരു്. പത്തൊന്‍പതാം നൂറ്റാണ്ടില്‍ മോര്‍ഫിയോടു തോറ്റ അദ്ദേഹം 1930-കളില്‍ അലക്സാണ്ടര്‍ അലക്കൈനോടും വയസ്സുകാലത്തു തോറ്റിട്ടുണ്ടു്. തോറ്റെങ്കിലും ഇത്ര വയസ്സുകാലത്തും കളിക്കുന്ന അയാളോടു് എനിക്കു ബഹുമാനം തോന്നിയിരുന്നു-അതും ലോകത്തിന്റെ വിവിധഭാഗങ്ങളില്‍ ചുറ്റി നടന്നു കളിച്ചിരുന്ന ആ അര്‍പ്പണബോധത്തെ ഓര്‍ത്തിട്ടു്.

പിന്നീടു മറ്റൊരു പുസ്തകത്തില്‍ ഇദ്ദേഹം ബോബി ഫിഷറിനോടു് 1960-കളില്‍ തോല്‍ക്കുന്നതു കണ്ടപ്പോഴാണു് എന്തോ പാകപ്പിഴയുണ്ടെന്നു മനസ്സിലായതു്. പിന്നെ മനസ്സിലായി പേരു പ്രസക്തമല്ലാത്ത വെറും കളിക്കാരെ (വലിയ കളിക്കാര്‍ സൈമല്‍ട്ടേനിയസ്സ് എക്സിബിഷനിലും മറ്റും കളിക്കുന്നവര്‍) സൂചിപ്പിക്കാന്‍ സാധാരണ ഉപയോഗിക്കുന്ന പേരാണു് Amateur എന്നു്.

പില്‍ക്കാലത്താണു് മാക്സ് ഓയ്‌വിന്റെ Master vs Amateur, Road to the Chess Mastery എന്നീ പുസ്തകങ്ങള്‍ വായിച്ചതു്.

---

ജോലി തെണ്ടിയും പിന്നെ കിട്ടിയും ബോംബെയില്‍ മൂന്നു സഹമുറിയന്മാരൊപ്പം താമസിക്കുന്ന സമയത്തു വീട്ടില്‍ ഇംഗ്ലീഷ് പത്രം വരുത്തുമായിരുന്നു. ടൈംസ് ഓഫ് ഇന്ത്യ. ഇന്നത്തെയും എന്നത്തെയും പോലെ അന്നും എനിക്കു പത്രവായനയുടെ ദുശ്ശീലമില്ല. (ഈയിടെ കാലിഫോര്‍ണിയയില്‍ തീപിടുത്തമുണ്ടായതറിഞ്ഞതു രാം മോഹന്റെ പോസ്റ്റു കണ്ടപ്പോഴാണു്. മൂട്ടില്‍ ചൂടു തട്ടിയപ്പോഴല്ല, ഭാഗ്യം!) ഞായറാഴ്ച വേറേ ഒന്നും ചെയ്യാനില്ലാത്തതു കൊണ്ടു വാരഫലം, കാര്‍ട്ടൂണുകള്‍, മുകുല്‍ ശര്‍മ്മയുടെ “മൈന്‍ഡ് സ്പോര്‍ട്ട്”, ചെസ്സ്, ബ്രിഡ്ജ് തുടങ്ങിയവ വായിക്കും. അത്രമാത്രം.

താത്പര്യത്തോടു കൂടി ആകെ വായിക്കുന്നതു വേറേ ഏതോ ദിവസം പ്രസിദ്ധീകരിക്കുന്ന വിവാഹപ്പരസ്യങ്ങള്‍ മാത്രമാണു്. പരസ്യത്തിനു മറുപടി അയയ്ക്കാന്‍ ഉദ്ദേശ്യമൊന്നുമില്ല. എങ്കിലും കെട്ടുപ്രായമായ പെങ്കൊച്ചുങ്ങള്‍ക്കും അവരുടെ അപ്പനമ്മമാര്‍ക്കും വരന്‍ എങ്ങനെയുള്ളവനാകണം? എന്നതിനെപ്പറ്റിയുള്ള അഭിപ്രായം അറിയാന്‍ ഒരു കൊതി. അതുപോലെ ആകാന്‍ ശ്രമിക്കാം എന്ന ദുരുദ്ദേശ്യമൊന്നുമില്ല താനും.

അങ്ങനെ നോക്കിയിരിക്കുമ്പോഴാണു് മിക്കവാറും എല്ലാ പരസ്യത്തിലും ഉള്ള ഒരു വാക്കു കണ്ണില്‍ തറച്ചതു്. പയ്യന്‍ teetotaler ആയിരിക്കണമത്രേ!

സഹമുറിയന്‍ വാങ്ങി വെച്ച ഒരു നിഘണ്ടു അലമാരയിലുണ്ടു്. ഈ വക കാര്യങ്ങളില്‍ ഞാന്‍ അതു തൊട്ടുനോക്കാറു പോലുമില്ല. (അതിനു വേറേ ഒരു കാരണം കൂടിയുണ്ടു്. അതു് ഇംഗ്ലീഷ്-ഇംഗ്ലീഷ് നിഘണ്ടുവാണു്, ഇംഗ്ലീഷ്-മലയാളം അല്ല. അതില്‍ അറിയാത്ത ഒരു വാക്കിന്റെ അര്‍ത്ഥം നോക്കിയാല്‍ അറിയാത്ത വേറെ അഞ്ചു വാക്കു കിട്ടും. അവയുടെ അര്‍ത്ഥം നോക്കിയാല്‍ നമ്മുടെ അണ്‍നോണ്‍ വൊക്കാബുലറിയില്‍ ഇരുപത്തഞ്ചു വാക്കുകളാകും. അങ്ങനെ അര്‍ജ്ജുനന്റെ അമ്പുകള്‍ പോലെ എടുക്കുമ്പോള്‍ ഒന്നു്, തൊടുക്കുമ്പോള്‍ പത്തു് എന്നിങ്ങനെ അറിയാത്ത വാക്കുകള്‍ കൂടിക്കൊണ്ടിരിക്കും.) പകരം, സ്വന്തം അതീന്ദ്രിയദ്ധ്യാനം തന്നെ ഉപയോഗിക്കും. ആ വാക്കു കണ്ടിട്ടു നല്ല മെലിഞ്ഞു നീണ്ട ഒരുവനാണെന്നു തോന്നി. Toe വരെ total ആയി എത്തുന്ന കൈയുള്ളവന്‍ എന്നോ മറ്റോ ഒരര്‍ത്ഥവും തോന്നി. അതുകൊണ്ടു മെലിഞ്ഞുനീണ്ടവന്‍ എന്നൊരു അര്‍ത്ഥമെടുത്തു. ആജാനുബാഹു എന്നു വേണമെങ്കില്‍ ഒരു വെയിറ്റിനു പറയാം എന്നും ഓര്‍ത്തു.

എന്തിനും സംശയം ചോദിക്കുന്ന ഒരുവന്‍ മുറിയില്‍ വന്നതും അവന്‍ പത്രം വായിച്ചതും (അവന്‍ പത്രം മുഴുവന്‍ പരസ്യമുള്‍പ്പെടെ അരിച്ചുപെറുക്കി വായിക്കും) ഇതിന്റെ അര്‍ത്ഥം ചോദിച്ചതും ഞാന്‍ “ആജാനുബാഹു” എന്നു പറഞ്ഞതും എല്ലാവരും തലയറഞ്ഞു ചിരിച്ചതും പിന്നെ കുറേക്കാലം എന്നെ എല്ലാവരും “ആജാനുബാഹു” എന്നു വിളിച്ചതും ഒക്കെ ഇന്നലെ കഴിഞ്ഞതു പോലെ തോന്നുന്നു. ഓര്‍മ്മകളേ….

(എന്നെപ്പോലെ മടിയുള്ളവര്‍ക്കു വേണ്ടി: teetotaler എന്നു വെച്ചാല്‍ ഒരു കാലത്തും മദ്യപിക്കില്ല എന്നു പ്രതിജ്ഞയെടുത്തവന്‍ എന്നാണര്‍ത്ഥം.)

---

ഇനിയുമുണ്ടു് ഒരുപാടു പോസ്റ്റുകളെഴുതാനുള്ള വകുപ്പു് ഈ വിഷയത്തില്‍. ഞാന്‍ ഏതായാലും തത്ക്കാലം ഇവിടെ നിര്‍ത്തുന്നു. ഇതിന്റെ മൂന്നാം ഭാഗം അരവിന്ദനും നാലാം ഭാഗം വിശാലമനസ്കനും എഴുതും എന്നറിയുന്നു. ഒരു പക്ഷേ, ഇതു ബൂലോഗത്തിലെ ആദ്യത്തെ സംയുക്തപരമ്പരയാവില്ല എന്നാരു കണ്ടു? ഇതായിരിക്കുമോ ബൂലോഗത്തില്‍ നിന്നുള്ള അടുത്ത പുസ്തകം? “ബൂലോഗരുടെ അബദ്ധധാരണകള്‍”!

അബദ്ധധാരണകളുടെ ഇനിയുള്ള ഭാഗങ്ങള്‍ എഴുതുന്നവരുടെ പ്രത്യേക ശ്രദ്ധയ്ക്കു്:

1. നാമെഴുതുന്നതു് ആരോടെങ്കിലും ചോദിച്ചു മനസ്സിലാക്കാവുന്ന സംഗതികള്‍ മടി കൊണ്ടോ ജീന്‍ ഇല്ലാത്തതു കൊണ്ടോ ചെയ്യാതെ വളരെക്കാലം കൊണ്ടു് അബദ്ധത്തില്‍ ചാടുന്ന സംഗതികളാണു്. അല്ലാതെ അറിവില്ലായ്മ കൊണ്ടും അധികപ്രസംഗം കൊണ്ടും കാണിക്കുന്ന മണ്ടത്തരങ്ങളല്ല. അത്തരം സംഗതികള്‍ക്കായി ശ്രീജിത്ത് “മണ്ടത്തരങ്ങള്‍” എന്ന ബ്ലോഗ് തുറന്നു വെച്ചിട്ടുണ്ടു്. അതിപ്പോള്‍ ലീസിനു ലഭ്യമാണു്.
2. മുകളില്‍ പറഞ്ഞ കാരണം കൊണ്ടു് അനംഗാരിയും വെമ്പള്ളിയും പറഞ്ഞ മാതിരിയുള്ള ഉദാഹരണങ്ങള്‍ സ്വീകാര്യമല്ല.
3. ഓവറാക്കരുതു്. സത്യം സത്യമായേ പറയാവൂ.

ആശംസകള്‍!

ഭൂരിഭാഗം കുട്ടികള്‍ക്കുള്ള ഒരു ഗുണം എനിക്കു ചെറുപ്പത്തില്‍ ഉണ്ടായിരുന്നു. അറിയില്ല എന്നു നാലാള്‍ അറിയുന്നതിലുള്ള ചമ്മല്‍. അതുകൊണ്ടു് അറിയാത്ത എന്തെങ്കിലും കേട്ടാല്‍ അതു ചോദിച്ചു മനസ്സിലാക്കുന്ന സ്വഭാവമില്ല. വായിച്ചോ വേറെ ആരോടെങ്കിലും ചോദിച്ചോ അതീന്ദ്രിയദ്ധ്യാനം നടത്തിയോ ടി കാര്യം പിന്നീടു ഗ്രഹിച്ചുകൊള്ളാം എന്നങ്ങു തീരുമാനിക്കും. പിന്നെ ആ വഴിക്കു പോകുന്ന പ്രശ്നമില്ല. കുറേ കഴിയുമ്പോള്‍ താന്‍ തന്നെ മേല്‍പ്പറഞ്ഞ അതീന്ദ്രിയദ്ധ്യാനത്തിലൂടെ കണ്ടുപിടിച്ച സംഗതി ശരിയാണെന്നങ്ങു് ഉറപ്പിക്കും. അതു മഹാ അബദ്ധവുമായിരിക്കും.

വലുതായിട്ടും ഈ സ്വഭാവം മാറിയില്ല. അറിയാത്ത കാര്യങ്ങള്‍ ക്ലാസ്സില്‍ സാറിനോടു ചോദിക്കില്ല. ആചാര്യനല്ലാതെ വിദ്യ നേടാന്‍ നാലില്‍ മൂന്നു കാര്യങ്ങളുണ്ടല്ലോ എന്നു കരുതി അങ്ങു വിടും. അവസാനം അവയില്‍ അതെല്ലാം വിട്ടിട്ടു് കാലക്രമം കൊണ്ടു് അതു കിട്ടുമ്പോഴേയ്ക്കു പശു ചത്തു മോരിലെ പുളിയും പോയി എന്ന സ്ഥിതിയാകും.

ജോലിസ്ഥലത്താണു് ഏറ്റവും ബുദ്ധിമുട്ടിയതു്. സിവില്‍ എഞ്ചിനീയറിംഗില്‍ ബിരുദവും ട്രാന്‍സ്പോര്‍ട്ടെഷന്‍ ആന്‍ഡ് ട്രാഫിക് എഞ്ചിനീയറിംഗില്‍ ബിരുദാനന്തരബിരുദവുമെടുത്തിട്ടു് അവയോടു പുലബന്ധം പോലുമില്ലാത്ത കമ്പ്യൂട്ടര്‍ പ്രോഗ്രാമറായി ജോലി തുടങ്ങിയ എന്നെത്തേടിയെത്തിയ പ്രോജക്ടുകളില്‍ പലതിലും (ടെലഫോണ്‍ സ്വിച്ചിംഗ് ടെക്നോളജി, മ്യൂച്വല്‍ ഫണ്ട്സ്, ഹാര്‍ഡ്വെയര്‍ മോഡങ്ങളുടെ എംബഡഡ് സോഫ്റ്റ്വെയര്‍, ഇലക്ട്രോണിക് ഡിസൈന്‍ ഓട്ടോമേഷന്‍ തുടങ്ങി യൂണിക്കോഡ് വരെ) അറിയുന്നതില്‍ കൂടുതലും അറിയാ‍ത്തതായിരുന്നു. വായിച്ചറിയാം എന്നു കരുതി ചോദ്യങ്ങള്‍ ചോദിക്കാതിരുന്നിടത്തൊക്കെ അത്യാഹിതങ്ങള്‍ പലതും സംഭവിച്ചു. ഏതായാലും കുറെക്കാലമായി സംശയങ്ങള്‍ മടി വിട്ടു ചോദിക്കാന്‍ കഴിയുന്നുണ്ടു്. അതിനു സാദ്ധ്യമായതില്‍ പിന്നെയാണു ജോലിയില്‍ അല്പം സമാധാനമായതു്.

എന്റെ ഗ്രാമത്തില്‍ എനിക്കു മുമ്പുള്ള കുറേ തലമുറകളിലുള്ള ആളുകള്‍ക്കൊരു പ്രത്യേകതയുണ്ടായിരുന്നു. അധികം ദൂരെപ്പോയി വിവാഹം കഴിക്കാന്‍ അധികം പേര്‍ക്കും താത്പര്യമുണ്ടായിരുന്നില്ല. അതിനാല്‍ മിക്കവാറും ആളുകളും സ്വഗ്രാമമായ ഇലന്തൂര്‍, അടുത്ത ഗ്രാമമായ ഓമല്ലൂര്‍ എന്നീ സ്ഥലങ്ങളില്‍ നിന്നു തന്നെ കല്യാണം കഴിച്ചു സസുഖം വാണു. പത്തു കിലോമീറ്ററില്‍ കൂടുതല്‍ ദൂരത്തു നിന്നു ഇവിടെ വന്നു കല്യാണം കഴിച്ചവരെ “വരത്തര്‍” എന്നു വിളിച്ചു. അവരുടെ നാടിനെ കടപ്പുറമെന്നോ മലമ്പ്രദേശമെന്നോ അവര്‍ വന്ന ദിശയെ എക്സ്ട്രാപൊളേറ്റ് ചെയ്തു വിവക്ഷിച്ചു.

ഇതുമൂലം വലഞ്ഞതു് സംശയപൂരണത്തില്‍ പിന്നോക്കമായിരുന്ന ഞാനാണു്. കാണുന്ന മിക്കവാറും മുഖങ്ങളൊക്കെ ബന്ധുക്കളാണു്. എന്നാല്‍ അവരുടെ പേരു്, ബന്ധം, എന്താണു് അവരെ വിളിക്കേണ്ടതു്, അവരുടെ മാതാപിതാപുത്രകളത്രങ്ങള്‍ ആരൊക്കെ എന്നിവയെപ്പറ്റി എനിക്കൊരു ഗ്രാഹ്യവുമില്ല. ജനിച്ചപ്പോള്‍ മുതല്‍ കാണുന്ന ആളുകളോടു് “നിങ്ങളാരാ?” എന്നെങ്ങനെ ചോദിക്കും? അമ്മയോടെങ്ങാനും രഹസ്യമായി ചോദിച്ചാല്‍ പിന്നെ കുശാലായി. അയാളുടെ മുന്നില്‍ വെച്ചു തന്നെ അമ്മ ഉറക്കെ തമാശ പറയും: “ദേ, കേട്ടോ, ഇവനു കൊച്ചാട്ടന്‍ ആരാണെന്നു് അറിയില്ലെന്നു്. ഇവനെപ്പോലൊരു കൊജ്ഞാണന്‍!” (കൊജ്ഞാണന്‍ എന്നതു ബുദ്ധിരാക്ഷസന്‍, സര്‍വ്വജ്ഞന്‍ തുടങ്ങിയവയുടെ വിപരീതപദമാകുന്നു.)

സായിപ്പിന്റെ നാട്ടിലാണെങ്കില്‍ അങ്കിള്‍ എന്നോ ആന്റി എന്നോ പറഞ്ഞു തടി തപ്പാവുന്ന ബന്ധങ്ങളില്‍ പലതും ഇവിടെ വളരെ സങ്കീര്‍ണ്ണമാണു്. അച്ഛന്റെ ജ്യേഷ്ഠന്റെ സ്ഥാനത്തുള്ളവരെ പേരപ്പന്‍ എന്നും അനിയന്റെ സ്ഥാനത്തുള്ളവരെ ചിറ്റപ്പന്‍ എന്നും വിളിക്കണം. (ഈ സ്ഥാനം കണ്ടുപിടിക്കാന്‍ നാലു തലമുറ പുറകോട്ടു പോയി ഒരു സാഹോദര്യം കണ്ടുപിടിച്ചിട്ടു തിരിച്ചു വരണം.) അച്ഛന്റെ സഹോദരിയുടെ സ്ഥാനത്തുള്ള സ്ത്രീ അപ്പച്ചിയാണു്. അതു തന്നെ മൂത്തതാണെങ്കില്‍ വല്യപ്പച്ചി, ഇളയതാണെങ്കില്‍ കൊച്ചപ്പച്ചി. അമ്മയുടെ സഹോദരസ്ഥാനത്തുള്ളവര്‍ അമ്മാവന്‍ (അമ്മാവന്‍, കുഞ്ഞമ്മാവന്‍, ഗോപാലകൃഷ്ണനമ്മാവന്‍ എന്നിങ്ങനെ പല രൂപവുമുണ്ടു് അതിനു്), പേരമ്മ, കൊച്ചമ്മ/കുഞ്ഞമ്മ/ചിറ്റമ്മ (ഇതിലേതു വേണമെന്നു വിളിക്കപ്പെടേണ്ടവരുടെ ഇഷ്ടമനുസരിച്ചു മാറും) എന്നിങ്ങനെ. അതിനും മുമ്പുള്ള തലമുറ അപ്പൂപ്പനും അമ്മൂമ്മയും. ഭാഗ്യത്തിനു് അച്ഛന്‍ വഴിയ്ക്കും അമ്മ വഴിയ്ക്കും വെവ്വേറേ പേരില്ല. എങ്കിലും അച്ഛന്റെയോ അമ്മയുടേയോ അമ്മാവന്റെ/അമ്മായിയുടെ സ്ഥാനത്തുള്ള ആളെ വല്യമ്മാവന്‍/വല്യമ്മായി എന്നേ വിളിക്കാവൂ. ഒരേ ഡെസിഗ്നേഷന്‍ (ഉദാ: വല്യമ്മായി) പലരുണ്ടാകാമെന്നതുകൊണ്ടു് ഒരാളെപ്പറ്റി മറ്റൊരാളോടു പറയുമ്പോള്‍ വീട്ടുപേരും ചിലപ്പോള്‍ ആളിന്റെ പേരും ചേര്‍ത്തും പറയണം. വല്യതറയിലെ പുരുഷോത്തമന്‍ ചിറ്റപ്പന്‍, ഇളം‌പ്ലാവിലെ ദാമോദരനമ്മാവന്‍ എന്നിങ്ങനെ.

ഏറ്റവും ബുദ്ധിമുട്ടു ജരാ‍നരകള്‍ ബാധിച്ച ചില മനുഷ്യരുടെ കാര്യമാണു്. ഏതു കണ്ണുപൊട്ടനും അപ്പൂപ്പാ എന്നു വിളിക്കും. പക്ഷേ കണക്കെടുത്താല്‍ അയാള്‍ നമ്മുടെ ഒരു ചേട്ടനായി വരും. അതിനാല്‍ കൊച്ചാട്ടാ എന്നേ വിളിക്കാവൂ. ചേച്ചിമാരെ ഇച്ചേയീ എന്നും.

ചിലര്‍ ഒരേ സമയത്തു രണ്ടായിരിക്കും. വെള്ളമടിക്കാതെ തന്നെ. അച്ഛന്‍ വഴിക്കു ചിറ്റപ്പനും അമ്മ വഴിക്കു് അമ്മാവനും ഒരാള്‍ തന്നെയാവാം. (നാലഞ്ചു തലമുറകള്‍ കൊണ്ടുള്ള സാഹോദര്യമാണെന്നോര്‍ക്കണം. അല്ലാതെ പെരിങ്ങോടന്‍ പറയുന്ന അഗമ്യഗമനമല്ല.) ഈ സന്ദര്‍ഭത്തില്‍ എന്തു വിളിക്കണം എന്നതു വളരെ കോമ്പ്ലിക്കേറ്റഡ് ആയ ഒരു അല്‍ഗരിതം ആണു്. എനിക്കിതു വരെ മനസ്സിലായിട്ടില്ല. ഇതില്‍ ഏറ്റവും അടുത്ത ബന്ധം നോക്കുകയോ മറ്റോ ആണു്. അതൊന്നും വ്യക്തമാകാത്തതു കൊണ്ടു് “പുസ്തകത്തില്‍ ഇടത്തു വശത്തുള്ളതു് ഉപമ, വലത്തു വശത്തുള്ളതു് ഉത്പ്രേക്ഷ” എന്നു പിള്ളേര്‍ കാണാതെ പഠിക്കുന്നതു പോലെ ഗോപാലകൃഷ്ണനമ്മാവന്‍, വിശ്വനാഥന്‍ ചിറ്റപ്പന്‍ എന്നിങ്ങനെ ഉരുവിട്ടു പഠിച്ചു കഷ്ടിച്ചു രക്ഷപ്പെട്ടു പോന്നു.

ചുരുക്കം പറഞ്ഞാല്‍ ആളുകളുടെ പേരു്, ബന്ധം (through shortest-path algorithm), പ്രായം, ജോലിസ്ഥലം തുടങ്ങി ധാരാളം വിവരങ്ങള്‍ അറിയാമെങ്കിലേ നിന്നു പിഴയ്ക്കാന്‍ പറ്റൂ. എനിക്കിതു വലിയ ബുദ്ധിമുട്ടായിരുന്നു. അതിനാല്‍ “ഓമല്ലൂരെങ്ങാണ്ടുള്ള, നരച്ച താടിയുള്ള, എല്ലാ സദ്യയ്ക്കും ആദ്യത്തെ പന്തിയ്ക്കു തന്നെയിരിക്കുന്ന ഒരു അപ്പൂപ്പനോ പേരപ്പനോ ആരാണ്ടില്ലേ, അങ്ങേരു്” എന്നൊക്കെയാണു് എന്റെ വിവരണം പലപ്പോഴും.

ബന്ധുക്കള്‍ക്കു മാത്രമല്ല ഈ പ്രശ്നം. നാട്ടില്‍ നൂറു വികാരിയച്ചന്മാരുണ്ടു്. എല്ലാവര്‍ക്കും ളോഹയുണ്ടു്, ബെല്‍റ്റുണ്ടു്, താടിയുണ്ടു്, ചുണ്ടില്‍ പുഞ്ചിരിയുണ്ടു്, കക്ഷത്തില്‍ ബൈബിളുണ്ടു്. ഏതച്ചനാ‍ണെന്നു പറയാന്‍ എനിക്കു യാതൊരു നിര്‍വ്വാഹവുമില്ല. എന്നാല്‍ അച്ചനോടു ചോദിച്ചാല്‍ പോരേ പേരെന്താണെന്നോ ഏതു പള്ളിയിലെയാണെന്നോ. ങ്ങേ ഹേ! അച്ചനെന്തു വിചാരിക്കും!

അറിയാത്തതു ചോദിക്കാനുള്ള മടിയുടെ ഉത്തരവാദിത്വം ഞാന്‍ അവസാനം മാതാപിതാക്കളിലാണു ഞാന്‍ ആരോപിച്ചതു്. ആ സ്വഭാവത്തിനുള്ള ജീന്‍ അവര്‍ എനിക്കു തരാഞ്ഞതാണു് അതിനു കാരണം എന്നായിരുന്നു എന്റെ കണ്ടുപിടിത്തം. (ഏതായാലും ആ ജീനാണോ അമ്മ വഴിക്കു കിട്ടിയ ജീനാണോ എന്തോ, എന്റെ മകനു് അറിയാത്തതു ചോദിക്കാനുള്ള സ്വഭാവം കിട്ടിയിട്ടുണ്ടു്.)

സംശയം ചോദിക്കാനുള്ള ജീനിന്റെ അഭാവം മൂലം വന്നുകൂടിയ അസംഖ്യം അബദ്ധധാരണകളില്‍ നിന്നു തിരഞ്ഞെടുത്ത ഏതാനും മുത്തുമണികളാണു താഴെ.

---

എന്റെ ഓര്‍മ്മയില്‍ ഞാന്‍ ആദ്യമായി വായിക്കുന്ന പത്രവാര്‍ത്ത “ഇന്ത്യയുമായി യുദ്ധത്തിനു പാക്കിസ്താന്‍ ഒരുങ്ങിനില്‍ക്കുന്നു” എന്നു മാതൃഭൂമിയില്‍ വന്ന വാര്‍ത്തയാണു്. 1971-ലായിരിക്കണം. അപ്പോള്‍ എനിക്കു പ്രായം അഞ്ചോ ആറോ. അതിനു മുമ്പു തന്നെ ഇന്ത്യയുടെ ഭൂപടവും അതിന്റെ മുകളില്‍ ഇടത്തുവശത്തായി കിടക്കുന്ന പാക്കിസ്ഥാനെയും കണ്ടിട്ടുണ്ടായിരുന്നു. മുഖലക്ഷണം പറയുന്ന കാക്കാത്തിയുടെ തോളത്തിരിക്കുന്ന തത്തയെപ്പോലെ ഇന്ത്യയുടെ തോളത്തിരിക്കുന്ന ഒരു ജീവിയായാണു ഞാന്‍ അന്നു പാക്കിസ്ഥാനെ കരുതിയിരുന്നതു്. ആ ജീവിക്കു് ഇന്ത്യയോടു യുദ്ധം ചെയ്യാന്‍ എന്തൊരു ധൈര്യമാണെന്നു് അദ്ഭുതപ്പെടുകയും ചെയ്തു.

“ഒരുങ്ങിനില്‍ക്കുന്നു” എന്ന പ്രയോഗമാണു കൂടുതല്‍ കൗതുകമുണര്‍ത്തിയതു്. എവിടെയെങ്കിലും പോകുന്നതിനു തൊട്ടുമുമ്പു് എന്റെ അമ്മ (കര്‍മ്മണിപ്രയോഗത്തിന്റെ പ്രഖ്യാപിതശത്രുവായ ബെന്നി ദയവായി ഈ വാക്യത്തിന്റെ ബാക്കി ഭാഗം വിട്ടു വായിക്കുക.) ഭിത്തിയില്‍ രണ്ടാണികളില്‍ താങ്ങപ്പെട്ട കീഴ്‌ഭാഗവും വലിഞ്ഞുനില്‍ക്കുന്ന ഒരു ചരടിനാല്‍ മറ്റൊരാണിയോടു ബന്ധിതമായ മുകള്‍ഭാഗവുമുള്ള, ലംബദിശയോടു് ഏകദേശം 30 ഡിഗ്രിയില്‍ ചരിഞ്ഞുനില്‍ക്കുന്ന, കണ്ണാടിക്കു മുമ്പില്‍ നിന്നു മുഖത്തു പൗഡറിടുന്ന പ്രക്രിയയെയാണു് അന്നു വരെ ഒരുങ്ങുക എന്ന പദത്തിന്റെ അര്‍ത്ഥമായി ഞാന്‍ മനസ്സിലാക്കിയിരുന്നതു്. ഇന്ത്യയോടു യുദ്ധം ചെയ്യാന്‍ ഇന്ത്യയുടെ വലത്തു തോളിലിരുന്നു് ഇന്ത്യയുടെ ചെവിയിലോ മറ്റോ തൂക്കിയിട്ടിരിക്കുന്ന കണ്ണാടിയില്‍ നോക്കി മുഖത്തു പൗഡറിടുന്ന പാക്കിസ്ഥാനെ ഞാന്‍ മനസ്സില്‍ കണ്ടു. ഇന്ത്യാ-പാക്ക്‌ യുദ്ധത്തെപ്പറ്റി കേള്‍ക്കുമ്പോള്‍ ഇന്നും എന്റെ മനസ്സില്‍ വരുന്ന ചിത്രം ഇതാണു്.

---

ആദ്യം വായിച്ച പത്രവാര്‍ത്ത ഇന്ത്യാ-പാക്ക് യുദ്ധമാണെങ്കിലും, അതിനു മുമ്പു തന്നെ പത്രം കാണുകയും വലിയവര്‍ വായിക്കുന്ന വാര്‍ത്തകള്‍ കേള്‍ക്കുകയും ചെയ്യുമായിരുന്നു. അങ്ങനെയുള്ളവയില്‍ ഏറ്റവും ആദ്യത്തേതായി മനസ്സില്‍ തങ്ങിനില്‍ക്കുന്നതു് മനുഷ്യന്‍ ചന്ദ്രനിലിറങ്ങിയ വാര്‍ത്തയാണു്. അതിന്റെ പടങ്ങള്‍ പത്രത്തില്‍ കണ്ടതു് നല്ല ഓര്‍മ്മയുണ്ടു്. എന്റെ അമ്മയുടെ അഭിപ്രായത്തില്‍ കഴിഞ്ഞ നൂറ്റാണ്ടിലെ ഏറ്റവും വലിയ രണ്ടു വാര്‍ത്തകള്‍ ഇന്ത്യയ്ക്കു സ്വാതന്ത്ര്യം കിട്ടിയതും മനുഷ്യന്‍ ചന്ദ്രനിലിറങ്ങിയതുമാണു്. അവ രണ്ടും പോലെ മനുഷ്യരെ ആകര്‍ഷിച്ച മറ്റൊരു വാര്‍ത്തയും ഉണ്ടായിട്ടില്ലത്രേ. മൂന്നാമത്തെ വാര്‍ത്തയായ 1957-ലെ തെരഞ്ഞെടുപ്പും കമ്യൂണിസ്റ്റ് മന്ത്രിസഭ അധികാരത്തില്‍ വന്നതും ഇവയുടെ അടുത്തെത്തില്ലത്രേ.

പാക്കിസ്ഥാന്‍ ഇന്ത്യയോടു യുദ്ധത്തിനൊരുങ്ങിയ സമയത്തു തന്നെ നടന്ന സംഭവമാണു്. അന്നു് എന്റെ വീട്ടിനടുത്തുള്ള ഒരു അപ്പൂപ്പന്‍ അദ്ദേഹത്തിന്റെ വീട്ടില്‍ ഞായറാഴ്ചകളില്‍ ഒരു “ഗീതാക്ലാസ്” നടത്തിയിരുന്നു. പേരു് അങ്ങനെയാണെങ്കിലും അവിടെ ഭഗവദ്ഗീതയ്ക്കു പുറമേ ഹരിനാമകീര്‍ത്തനം, എഴുത്തച്ഛന്റെ അദ്ധ്യാത്മരാമായണം തുടങ്ങിയവയും പഠിപ്പിച്ചിരുന്നു. എന്റെ ചേച്ചിയും മറ്റു പല ചേച്ചിമാരും അവിടെ പഠിക്കാന്‍ പോകുമ്പോള്‍ ഞാനും കൂടെപ്പോകുമായിരുന്നു. കൊച്ചുകുട്ടിയായിരുന്നതു കൊണ്ടു് എന്നോടു പഠിക്കാന്‍ പറഞ്ഞിരുന്നില്ല. അപ്പൂപ്പന്റെ പഠനമുറിയിലുണ്ടായിരുന്ന ഭൂതക്കണ്ണാടി, ലാടകാന്തം തുടങ്ങിയവ എടുത്തു കളിക്കുകയായിരുന്നു എന്റെ വിനോദം. അതിനിടയില്‍ രാമായണവും ഹരിനാമകീര്‍ത്തനവുമൊക്കെ കുറേശ്ശെ കേള്‍ക്കും. കുറച്ചൊക്കെ മനസ്സിലാവും. മനസ്സിലാവാത്തതിനു തോന്നുന്ന അര്‍ത്ഥം മനസ്സിലാക്കും. വര്‍ഷങ്ങള്‍ക്കു ശേഷമാണു് അവയില്‍ പലതിന്റെയും അര്‍ത്ഥം മനസ്സിലാക്കിയതു്.

അങ്ങനെ കേട്ട ഒരു പദ്യമാണു് ഇതു്.

ഗര്‍ഭസ്ഥനായ് ഭുവി ജനിച്ചും മരിച്ചുമുദ-
കപ്പോള പോലെ ജനനാന്ത്യേന നിത്യഗതി
ത്വദ്ഭക്തിവര്‍ദ്ധനവുദിക്കേണമെന്‍ മനസി
നിത്യം തൊഴാമടികള്‍ നാരായണായ നമഃ

മനുഷ്യന്‍ ജനിക്കുന്നതിനു മുമ്പു് അമ്മയുടെ ഗര്‍ഭത്തില്‍ കുറച്ചു കാലം കിടക്കുന്നുണ്ടു് എന്നറിയാമായിരുന്നു. ഹിന്ദുമതക്ലാസ്സുകളും മതപ്രസംഗങ്ങളും മറ്റും കേള്‍ക്കുന്നതു കൊണ്ടു് മരിച്ചു കഴിഞ്ഞാല്‍ പിന്നെയും ജനിക്കുമെന്നും പിന്നെയും മരിക്കുമെന്നും അങ്ങനെ ഒരുപാടു ജനനമരണങ്ങള്‍ക്കു ശേഷം മോക്ഷം കിട്ടുമെന്നും കുറേശ്ശെ മനസ്സിലായിരുന്നു. അങ്ങനെ മോക്ഷം കിട്ടാന്‍ ദൈവഭക്തി വേണം. അതുണ്ടാവാന്‍ എന്നും ഈശ്വരന്റെ പാദങ്ങള്‍ തൊഴാം. ഇങ്ങനെ ശ്ലോകത്തിന്റെ അര്‍ത്ഥം വലിയ കുഴപ്പമില്ലാതെ മനസ്സിലാക്കി. ആകെ പ്രശ്നം വന്ന ഒരു വാക്കു് “അപ്പോള” ആണു്. (“ഉദ” എന്നതു് ബത, അപി, ച, ഹന്ത എന്നിവയെപ്പോലെ അര്‍ത്ഥം മനസ്സിലാക്കേണ്ടാത്ത ഒരു വാക്കാണെന്നു ഞാനങ്ങു തീരുമാനിച്ചു!) ഈ അപ്പോള പോലെയാണു ഗര്‍ഭത്തില്‍ കിടക്കുന്ന ശിശു മരിച്ചു സ്വര്‍ഗ്ഗത്തിലേക്കു പോകുന്നതു്.

ഈ അപ്പോള എന്താണെന്നതിനു് അത്ര വലിയ സംശയമൊന്നും തോന്നിയില്ല. സ്വര്‍ഗ്ഗത്തിലേയ്ക്കു് എളുപ്പം പോകാന്‍ സഹായിക്കുന്ന ഒരു വണ്ടിയാണു് അപ്പോള. ഈ അപ്പോളയില്‍ കയറിയാണു് അമേരിക്കക്കാര്‍ ഈയിടെ ചന്ദ്രനില്‍ പോയതു്. മരിക്കാന്‍ സമയമാവുമ്പോള്‍ ഏതോ വിമാനം വന്നു കൊണ്ടുപോകും എന്നൊക്കെയും പലയിടത്തും കേട്ടിട്ടുണ്ടു്. എല്ലാം കൂടി ചേര്‍ത്തു് ആലോചിച്ചപ്പോള്‍ സംഗതി ക്ലിയര്‍!

പിന്നീടെപ്പോഴോ കുങ്കുമം വാരികയില്‍ “ഉദകപ്പോള” എന്നൊരു നോവല്‍ (ആരെഴുതി എന്നോര്‍മ്മയില്ല, വായിച്ചിട്ടുമില്ല) കണ്ടപ്പോഴാണു് “അപ്പോള” അല്ല “ഉദകപ്പോള” ആണു വാക്കെന്നു മനസ്സിലായതു്. അമ്മയോടു ചോദിച്ചു് അര്‍ത്ഥം മനസ്സിലാക്കി. ഉദക+പോള = വെള്ളത്തിലെ കുമിള.

നീറ്റിലെപ്പോളയ്ക്കു തുല്യമാം ജീവിതം
പോറ്റുവാനെത്ര ദുഃഖിക്കുന്നു മാനുഷര്‍!

എന്ന കവിത പിന്നീടാണു കേട്ടതു്.

ഒരു യതിഭംഗം വരുത്തിയ വിന നോക്കണേ!

---

നാലാം ക്ലാസ്സിലോ ഏഴാം ക്ലാസ്സിലോ എത്തിയ അല്പസ്വല്പം പഠിക്കുന്ന സകലമാന പിള്ളേരുടെയും അന്നത്തെ ഒരു നിഷ്ഠയുണ്ടായിരുന്നു-സ്കോളര്‍ഷിപ്പു പരീക്ഷയ്ക്കു പഠിക്കല്‍. പിള്ളേരുടെ പ്രായത്തിനും അറിവിനും ഒതുങ്ങാത്ത ഒരു പറ്റം ചോദ്യങ്ങള്‍ ചോദിക്കുകയാണു് ഇതിന്റെ രീതി. മലയാളത്തില്‍ വ്യാകരണം, സാഹിത്യം, ലേഖനമെഴുതല്‍, സാഹിത്യചരിത്രം തുടങ്ങി വിവിധമേഖലകളിലെ വിജ്ഞാനം പരിശോധിക്കും. പഠിക്കുന്ന ക്ലാസ്സിനു മൂന്നു ക്ലാസ് മുകളിലുള്ള കണക്കുകളാണു് ഗണിതത്തിലെ ഉള്ളടക്കം. അതും നേരേ ചൊവ്വേ ചോദിക്കുകയില്ല. ബുദ്ധിപരീക്ഷ ബ്ലോഗിലെപ്പോലെ വളച്ചു കെട്ടിയേ ചോദിക്കൂ. ഇതിലും ഭീകരമാണു് ജെനറല്‍ നോളജ് എന്നാ സാധനം. ലോകവിജ്ഞാനം മുഴുവന്‍ അളക്കുന്ന ഈ പേപ്പറില്‍ (ഞാ‍ന്‍ എഴുതിയ വര്‍ഷം ശ്രീലങ്കയിലെ വിദേശകാ‍ര്യമന്ത്രി ആരാണെന്നു ചോദിച്ചിരുന്നു) അഞ്ചിലൊന്നില്‍ കൂടുതല്‍ ഒരു കുട്ടിയും എഴുതുക തന്നെയില്ല.

ഇനി ഇതെഴുതി കിട്ടിയാലോ, സര്‍ട്ടിഫിക്കറ്റില്ല, ട്രോഫിയില്ല, സമ്മാനമില്ല. ആകെ ഉള്ളതു് സ്കോളര്‍ഷിപ്പാണു്. ശിഷ്ടകാലത്തെ വിദ്യാഭ്യാസത്തിനുള്ള കാശു കിട്ടും എന്നു കരുതിയാല്‍ നിങ്ങള്‍ക്കു തെറ്റി. വര്‍ഷം തോറും 20 രൂപാ കിട്ടും. (കേരളത്തിലെ ആ‍ദ്യത്തെ 12-ല്‍ ഒരാളായാല്‍ നാഷണല്‍ സ്കോളര്‍ഷിപ്പു കിട്ടും. വര്‍ഷത്തില്‍ 150 രൂപാ!)

ഇങ്ങനെയൊക്കെയാണെങ്കിലും മിക്കവാറും എല്ലാ കുട്ടികളും ഇതെഴുതും. എന്തിനാണെന്നു ചോദിച്ചാല്‍, എല്ലാം വ്യര്‍ത്ഥമാണെന്നറിഞ്ഞിട്ടും ആളുകള്‍ ബുദ്ധിമുട്ടി മഴയും വെയിലുമേറ്റു ക്യൂ നിന്നു വോട്ടു ചെയ്യുന്നില്ലേ? അതുപോലെ ഒരു അഭ്യാസം.

ഇതിനു പഠിക്കാനായി അസ്സീസ്സി, വിദ്യാര്‍ത്ഥിമിത്രം, വി തുടങ്ങിയവര്‍ ഗൈഡുകള്‍ ഇറക്കിയിരുന്നു. എല്ലാ വിഷയത്തിന്റെയും ഗൈഡുകള്‍ ചേച്ചി പഠിച്ചതു് ഒരു കുഴപ്പവുമില്ലാതെ ലഭ്യമായതിനാല്‍ ഞാന്‍ മൂന്നാം ക്ലാസ്സിലേ പഠനം തുടങ്ങി. അന്നു മുതല്‍ പരീക്ഷയുടെ തലേ ആഴ്ച വരെ മലയാളം പഠിച്ചു. ഒരാഴ്ച കൊണ്ടു് കണക്കും ജെനറല്‍ നോളജും പഠിച്ചു പരീക്ഷയ്ക്കു പോയി. (ഏഴാം ക്ലാസ്സില്‍ ഇവ കൂടാതെ ഇംഗ്ലീഷ് എന്നൊരു സാധനം കൂടി ഉണ്ടെന്നറിഞ്ഞതു പരീക്ഷയുടെ ടൈം ടേബിള്‍ കിട്ടിയപ്പോഴാണു്.)

ബി. എ. നിലവാരത്തിലുള്ള മലയാളം പുസ്തകം രണ്ടു കൊല്ലം പഠിച്ചതിനാല്‍ എനിക്കു അതിഭീകരമായ ഭാഷാവിജ്ഞാനം സിദ്ധിച്ചു. ഗൈഡില്‍ കൊടുത്തിട്ടുള്ള എല്ലാ പദ്യങ്ങളും പഴഞ്ചൊല്ലുകളും കടങ്കഥകളും കാണാതെ പഠിച്ചു് ഉറക്കെ ചൊല്ലി നടന്നു ഞാന്‍ നാട്ടുകാരെ മുഴുവന്‍ ബുദ്ധിമുട്ടിച്ചു.

പദ്യങ്ങളില്‍ പലതിന്റെയും അര്‍ത്ഥം മനസ്സിലായിരുന്നില്ല. എല്ലാ കവികളുടെയും കവിതകളുണ്ടായിരുന്നു. ഒരു കവിയുടെ പേരു പറഞ്ഞു് അയാളുടെ നാലു വരി എഴുതാന്‍ പറഞ്ഞാല്‍ എഴുതണ്ടേ? അതിനാണു ഗൈഡുകാര്‍ അതെല്ലാം ഇട്ടതു്. (അതെല്ലാം ഇട്ടു ഗൈഡു വലുതായെങ്കിലല്ലേ കൂടുതല്‍ വില ഈടാക്കാന്‍ പറ്റൂ?)

അങ്ങനെ പഠിച്ച് കൂട്ടത്തില്‍ ചങ്ങമ്പുഴയുടേതായി ഈ കവിത കണ്ടു.

അങ്കുശമില്ലാത്ത ചാപല്യമേ, മന്നില്‍
അംഗനയെന്നു വിളിക്കുന്നു നിന്നെ ഞാന്‍!

അംഗന എന്നു വെച്ചാല്‍ സ്ത്രീ ആണെന്നറിയാം. മന്നു ഭൂമിയും. ചാപല്യത്തിന്റെ അര്‍ത്ഥവുമറിയാം. അങ്കുശം മാത്രം എന്താണെന്നൊരു പിടിയുമില്ല. എന്തോ ഇല്ലാത്ത ചാപല്യത്തിനെ ഭൂമിയില്‍ പെണ്ണെന്നു വിളിക്കുന്നു എന്നു മനസ്സിലായി. അമ്മ മലയാളാദ്ധ്യാപികയാണു്. ചോദിച്ചാല്‍ പറഞ്ഞു തരും. പക്ഷേ ചോദിച്ചു മനസ്സിലാക്കി അറിവു വര്‍ദ്ധിപ്പിക്കാനുള്ള ജീന്‍ പകര്‍ന്നു തരാത്ത അമ്മയോടു് എങ്ങനെ ചോദിക്കും? ങേ ഹേ!

സ്കോളര്‍ഷിപ്പുപുസ്തകത്തിന്റെ മറ്റൊരു സ്ഥലത്തു് കുത്തും കോമയും കൊടിലുമൊക്കെ പറയുന്ന സ്ഥലത്തു നിന്നു് ഉത്തരം കിട്ടി.

ചോദ്യചിഹ്നം അഥവാ കാകു	–	Question mark (?)
ആശ്ചര്യചിഹ്നം അഥവാ വിക്ഷേപിണി	–	Exclamation mark (!)
ശൃംഖല	–	Hyphen (-)
കോഷ്ഠം	–	Square brackets ([])
വലയം	–	Brackets (())
ഭിത്തിക	–	Colon (:)
അര്‍ദ്ധവിരാമം അഥവാ രോധിനി	–	Semi-colon (;)
പൂര്‍ണ്ണവിരാമം അഥവാ ബിന്ദു	–	Full stop (.)
അല്പവിരാമം അഥവാ അങ്കുശം	–	Comma (,)

“യുറീക്കാ” എന്നു ഞാന്‍ പറയാഞ്ഞതു് ആ വാക്കിനെപ്പറ്റി കേട്ടിട്ടില്ലാത്തതു കൊണ്ടു മാത്രമാണു്. (ആ പേരിലുള്ള ശാസ്ത്രമാസിക അന്നു പ്രസിദ്ധീകരിച്ചു തുടങ്ങിയിട്ടില്ല.) അങ്കുശം എന്നു വെച്ചാല്‍ കോമ. ഒരു കോമയും, അതായതു ചെറിയ ഒരു നിര്‍ത്തും, ഇല്ലാത്ത ചാപല്യമാണു് ഈ പെണ്ണെന്നു പറയുന്നതു്. ഈ ചങ്ങമ്പുഴയുടെ ഒരു വിവരമേ!

അങ്കുശം എന്നു പറയുന്നതു് ആനത്തോട്ടിയാണെന്നും ആനയ്ക്കു തോട്ടി പോലെയുള്ള യാതൊരു കണ്ട്രോളും ഇല്ലാത്ത ചാപല്യമാണു കവി അംഗനയില്‍ കെട്ടിവെച്ചതെന്നും ആനത്തോട്ടി പോലെയിരിക്കുന്നതു കൊണ്ടാണു കോമയെ അങ്കുശം എന്നു വിളിച്ചതെന്നും ചങ്ങമ്പുഴയുടെ കാലത്തിനും ശേഷമാണു് ആ പേര്‍ കോമയ്ക്കു വീണതെന്നും കാലം കുറെക്കഴിഞ്ഞിട്ടാണു് അറിഞ്ഞതു്.

എങ്കിലും ഇന്നും കോമയില്ലാത്ത ചാപല്യം എന്ന അര്‍ത്ഥം തന്നെയാണു് എനിക്കു് ആ പ്രയോഗത്തിനു കൂടുതല്‍ യോജിച്ച അര്‍ത്ഥമായി തോന്നുന്നതു്.

---

ഞാന്‍ ആദ്യമായി അമേരിക്കയിലെത്തിയ കാലം. ബിയറാണെന്നു കരുതി ഒരു വെന്‍ഡിംഗ് മെഷീനില്‍ നിന്നു റൂട്ട് ബിയര്‍ എടുത്തു കുടിച്ചിട്ടു “ഇതു കോള്‍ഗേറ്റ് ടൂത്ത്‌പേസ്റ്റു കലക്കിയ വെള്ളമാണല്ലോ” എന്നു പറഞ്ഞു തുപ്പിക്കളഞ്ഞ സംഭവം കഴിഞ്ഞിട്ടു് അധികം കാലമായിട്ടില്ല. അന്നു ജോലി ബോസ്റ്റണിലാ‍യിരുന്നു. ഒരു സുഹൃത്തിനോടൊപ്പം നയാഗ്ര കാണാന്‍ പോയി. കാറോടിക്കാനും മറ്റും അറിയില്ല. ഒരു ബസ്സില്‍ കയറി ബോസ്റ്റണില്‍ നിന്നു സിറക്യൂസില്‍ പോയി. അവിടെ സുഹൃത്തിന്റെ സുഹൃത്തുണ്ടു്. അവനും വേറേ ഒന്നുരണ്ടു സുഹൃത്തുക്കളും ചേര്‍ന്നു് ഒരു കാര്‍ റെന്റു ചെയ്തു് നയാഗ്രയിലേക്കു പോയി.

പോകുന്ന വഴിയ്ക്കു കാറിലെ റേഡിയോ വെച്ചപ്പോഴാണു വാര്‍ത്ത കേട്ടതു് – “ദിസ് ഈസ് റേഡിയോ ഒഷാവാ”. കര്‍ത്താവേ, ഞാന്‍ ഇത്രയും കാലം Ottawa എന്ന സ്ഥലത്തെ “ഒട്ടാവാ” എന്നാണല്ലോ വിളിച്ചിരുന്നതു്! വിവരമുള്ള ആരും അതു കേള്‍ക്കാഞ്ഞതു ഭാഗ്യം! സിറക്യൂസിനും നയാഗ്രയ്ക്കുമൊക്കെ വടക്കുഭാഗത്തു കിടക്കുന്ന ഒണ്ടേറിയോ തടാകത്തിന്റെ തൊട്ടു വടക്കു ഭാഗത്താണു കാനഡയുടെ തലസ്ഥാനമായ ഒട്ടാവ, തെറ്റി ഒഷാവ എന്ന ഭൂമിശാസ്ത്രവിജ്ഞാനം എനിക്കുണ്ടായിരുന്നു.

പൊടുന്നനേ അതീന്ദ്രിയദ്ധ്യാനത്തില്‍ നിന്നു കിട്ടിയ വിജ്ഞാനം ഞാന്‍ കാറിലുണ്ടായിരുന്നവരുമായി പങ്കു വെച്ചു. പിന്നീടു പലയിടത്തും വെച്ചു കണ്ടു മുട്ടിയ പലരോടും ആവശ്യമില്ലാതെ തന്നെ പറഞ്ഞു. അവരില്‍ പലരും ഈ വിജ്ഞാനം കുറെക്കൂടി വലിയ ഒരു ജനക്കൂട്ടത്തിനു പകര്‍ന്നു. “കൊടുക്കും തോറുമേറിടും” എന്നാണല്ലോ. അങ്ങനെ Ottawa-യുടെ ഉച്ചാരണം “ഒഷാവ” എന്നാണെന്നു ചിന്തിക്കുന്ന ഒരു വലിയ ജനതതിയെ തന്നെ എനിക്കു സൃഷ്ടിക്കുവാന്‍ കഴിഞ്ഞു.

ഇവ രണ്ടും രണ്ടു സ്ഥലങ്ങളാണെന്നു പിന്നീടു മനസ്സിലായപ്പോഴേയ്ക്കും ഒരു വലിയ ജനക്കൂട്ടം Ottava എന്നതിന്റെ യഥാര്‍ത്ഥ ഉച്ചാരണം ഒഷാവ എന്നാണെന്നു മനസ്സിലാക്കിക്കഴിഞ്ഞിരുന്നു. അറിവുള്ളവരോടു ചോദിക്കാതെ കേള്‍ക്കുന്നതൊക്കെ വിശ്വസിക്കുന്നവരുടെ കാര്യം എന്തു പറയാന്‍?

---

ഇനിയുമുണ്ടു ധാരാളം. Teetotaler എന്നു വെച്ചാല്‍ ആജാനുബാഹു എന്നാണര്‍ത്ഥമെന്നും, കുങ്ഫു എന്നതിന്റെ അര്‍ത്ഥം “മാരകമായ കൈ” എന്നാണെന്നും വെസ്റ്റ് ഇന്‍ഡീസ് എന്ന സ്ഥലം ഓസ്ട്രേലിയയുടെ അടുത്താണന്നും ഇസ്രയേല്‍ ആഫ്രിക്കയിലാണെന്നും തായ്‌വാനും തായ്‌ലന്‍ഡും ഒന്നാണെന്നും ഞാന്‍ വളരെക്കാലം കരുതിയിരുന്നു. കിം‌വദന്തിയെപ്പറ്റി ചെറുപ്പത്തിലേ കേട്ടിരുന്നതു കൊണ്ടു് ഏതായാലും അതൊരു ജന്തുവാണെന്നുള്ള പൊതുവായ ധാരണ എനിക്കുണ്ടായിരുന്നില്ല.

---

ഗുണപാഠം: അജ്ഞത ഒരു കുറ്റമല്ല. അറിയില്ല എന്നു പറയുന്നതു് മോശമായ കാര്യമല്ല. അതിനാല്‍ നമുക്കു നമ്മുടെ കുട്ടികളെ ചോദിച്ചു ചോദിച്ചു പോകാന്‍ പഠിപ്പിക്കാം.

കാളിദാസന്റെ അഭിജ്ഞാനശാകുന്തളം നാടകത്തില്‍ നിന്നൊരു ശ്ലോകം:

ആപരിതോഷാദ് വിദുഷാം
ന സാധു മന്യേ പ്രയോഗവിജ്ഞാനം
ബലവദപി ശിക്ഷിതാനാം
ആത്മന്യപ്രത്യയം ചേതഃ

അര്‍ത്ഥം:

പ്രയോഗവിജ്ഞാനം	:	പ്രയോഗിക്കുന്ന വിജ്ഞാനം
വിദുഷാം ആപരിതോഷാത്	:	വിദ്വാന്മാരുടെ അഭിനന്ദനം കിട്ടുന്നതു വരെ
സാധു ന മന്യേ	:	വിലയുള്ളതായി കരുതപ്പെടുന്നില്ല
ബലവത് ശിക്ഷിതാനാം അപി	:	നല്ലതുപോലെ പഠിച്ചവര്‍ക്കു പോലും
ചേതഃ ആത്മനി അപ്രത്യയം	:	മനസ്സു് ആത്മവിശ്വാസമില്ലാത്തതാണു്.

ബ്ലോഗെഴുത്തുകാര്‍ കമന്റു കാംക്ഷിക്കുന്നതു് ഇതുകൊണ്ടാണോ എന്നറിയില്ല. സീനിയര്‍ ബ്ലോഗര്‍മാര്‍ പുതിയ എഴുത്തുകാരെ തിരിഞ്ഞു നോക്കുന്നില്ല, പ്രോത്സാഹിപ്പിക്കുന്നില്ല എന്ന മുറവിളിയും കേള്‍ക്കാറുണ്ടു്. (എന്താണു് ഈ സീനിയര്‍/ജൂനിയര്‍/സബ് ജൂനിയര്‍ ബ്ലോഗര്‍‌മാരെന്നു് എനിക്കിതു വരെ പിടികിട്ടിയിട്ടില്ല.)

ആവാന്‍ വഴിയില്ല. ആണെങ്കില്‍ കുറേ പോസ്റ്റുകള്‍ എഴുതിക്കഴിയുമ്പോള്‍ ആത്മവിശ്വാസം കിട്ടുകയും കമന്റുകള്‍ക്കു വേണ്ടിയുള്ള മുറവിളി നിര്‍ത്തുകയും ചെയ്യേണ്ടതാണു്. ഇതിനു പറ്റിയ പദ്യം പൂന്താനത്തിന്റെ ജ്ഞാനപ്പാന അല്പം മാറ്റിയാല്‍ കിട്ടും.

എത്രയുണ്ടു കമന്റുകളെങ്കിലും
തൃപ്തിയായിടാ ബ്ലോഗര്‍ക്കൊരു കാലം;
പത്തു കിട്ടുകില്‍ നൂറു മതിയെന്നും
ശതമാകില്‍ സഹസ്രം മതിയെന്നും
ആയിരം കമന്റ് പോസ്റ്റിനുണ്ടാകിലും
അയുതമാകുകിലാശ്ചര്യമെന്നതും
ആശയായുള്ള പാശമതിങ്കേന്നു
വേറിടാതെ വലയുന്നു ബ്ലോഗര്‍മാര്‍
…
സ്ഥാനമാനങ്ങള്‍ ചൊല്ലിക്കലഹിച്ചു
നാണം കെട്ടു നടക്കുന്നിതു ചിലര്‍;
മദമത്സരം ചിന്തിച്ചു ചിന്തിച്ചു
മതി കെട്ടു നടക്കുന്നിതു ചിലര്‍;
ബ്ലോഗകങ്ങളില്‍ സേവകരായിട്ടു
കോലംകെട്ടി ഞെളിയുന്നിതു ചിലര്‍.
…
വിദ്യകൊണ്ടറിയേണ്ടതറിയാതെ
വിദ്വാനെന്നു നടിക്കുന്നിതു ചിലര്‍;
കുങ്കുമത്തിന്റെ ഗന്ധമറിയാതെ
കുങ്കുമം ചുമക്കുമ്പോലെ ഗര്‍ദ്ദഭം.
…
സത്തുക്കള്‍ ചെന്നിരന്നാലുമാക്കമ-
ന്റല്‌പമാത്രം കൊടാ ചില ദുഷ്‌ടന്മാര്‍
ചത്തുപോം നേരം ബ്ലോഗര്‍ പ്രൊഫൈല്‍ പോലു-
മൊത്തിടാ കൊണ്ടുപോവാനൊരുത്തര്‍ക്കും.
…
ഇന്നലെയോളമെന്തെന്നറിഞ്ഞീലാ
ഇന്നി നാളെയുമെന്തെന്നറിഞ്ഞീലാ
ഇന്നിക്കണ്ട ബ്ലോഗിന്നു വിനാശവു-
മിന്ന നേരമെന്നേതുമറിഞ്ഞീലാ.
…
കണ്ടാലൊട്ടറിയുന്നു ചിലരിതു
കണ്ടാലും തിരിയാ ചിലര്‍ക്കേതുമേ.
കണ്ടതൊന്നുമേ സത്യമല്ലെന്നതു
മുമ്പേ കണ്ടിട്ടറിയുന്നിതു ചിലര്‍.
…
കണ്ടു കണ്ടങ്ങിരിക്കും ജനങ്ങളെ-
ക്കണ്ടില്ലെന്നു വരുത്തുന്നതും ബ്ലോഗ്.
രണ്ടു നാലു ദിനംകൊണ്ടൊരുത്തനെ
തണ്ടിലേറ്റി നടത്തുന്നതും ബ്ലോഗ്.
മാളികമുകളേറിയ മന്നന്റെ
തോളില്‍ മാറാപ്പു കേറ്റുന്നതും ബ്ലോഗ്.
…
കുംഭമാസത്തിലാകുന്നു നമ്മുടെ
ജന്മനക്ഷത്രമശ്വതിനാളെന്നും
ശ്രാദ്ധമുണ്ടഹോ വൃശ്‌ചികമാസത്തില്‍
സദ്യയൊന്നുമെളുതല്ലിനിയെന്നും;
ഉണ്ണിയുണ്ടായി വേള്‍പ്പിച്ചതിലൊരു
ഉണ്ണിയുണ്ടായിക്കണ്ടാവു ഞാനെന്നും;
കോണിക്കല്‍ത്തന്നെ വന്ന നിലമിനി-
ക്കാണമെന്നന്നെടുപ്പിക്കരുതെന്നും,
ഇത്‌ഥമോരോന്നു ബ്ലോഗിയിരുന്നീടീല്‍
ഹിറ്റു കിട്ടാതെയായിടും ദൈവമേ!
…
കൂടിയല്ല നാം ബ്ലോഗുന്ന നേരത്തും
കൂടിയല്ല കമന്റുന്ന നേരത്തും
മദ്ധ്യേയിങ്ങനെ കാണുന്ന നേരത്തു
മത്സരിക്കുന്നതെന്തിനു നാം വൃഥാ?

🙂

---

ആര്യ എന്ന മാത്രാവൃത്തത്തിലുള്ള ഈ ശ്ലോകത്തിനു കേരളവര്‍മ്മ വലിയ കോയിത്തമ്പുരാന്റെ അനുഷ്ടുപ്പിലുള്ള പരിഭാഷ:

വിജ്ഞന്മാരഭിനന്ദിച്ചേ
വിജ്ഞാനം സാധുവായ് വരൂ;
നല്ല ശിക്ഷ കഴിച്ചോര്‍ക്കും
ഇല്ല വിശ്വാസമാത്മനി.

---

സ്കൂളില്‍ ചേര്‍ക്കാനും മറ്റും അത്യാവശ്യമായ വാക്സിനേഷനുകള്‍ ഒഴികെ ഒന്നും എനിക്കു കിട്ടിയിട്ടില്ല. എനിക്കറിയാവുന്ന പല ആളുകളുടെയും സ്ഥിതി അതാണു്. വാക്സിനേഷനുകള്‍ എടുക്കാഞ്ഞതു കൊണ്ടു് അവര്‍ക്കൊക്കെ രോഗപ്രതിരോധശക്തി കൂടിയിട്ടുണ്ടോ എന്നു് ഒരു പിടിയുമില്ല.

എന്നാല്‍ ഇപ്പോഴുള്ള കുട്ടികള്‍ക്കു് നാം ഡോക്ടര്‍ പറയുന്ന എല്ലാ വാക്സിനേഷനും കൊടുക്കുന്നുണ്ടു്. ഒരു രോഗത്തിന്റെ വലിയ ആഘാതത്തെ ചെറുക്കാന്‍ ആ രോഗം ഉണ്ടാക്കുന്ന അണുവിന്റെ ചെറിയ ഡോസ് കൊടുക്കുന്നതാണല്ലോ വാക്സിനേഷന്‍. ഇതു കുഞ്ഞുങ്ങള്‍ക്കു നല്ലതാണോ എന്നു ന്യായമായ ആശങ്ക ഉണ്ടാകാം.

മൂത്ത കുട്ടിക്കു് പല വൈകല്യങ്ങളും ഉണ്ടായ ഒരു സുഹൃത്തു് പറഞ്ഞ വിവരങ്ങള്‍ കേട്ടു ഞെട്ടിപ്പോയി. കുഞ്ഞുങ്ങള്‍ക്കു കൊടുക്കുന്ന MMR, reubella തുടങ്ങിയ വാക്സിനുകളില്‍ ടോക്സിക് പദാര്‍ത്ഥങ്ങള്‍ ഉണ്ടത്രേ! എല്ലാ കുട്ടികള്‍ക്കും അതു നല്ലതല്ല. ചില കുട്ടികളെ അതു വലുതായി ബാധിക്കും. Autism തുടങ്ങിയ രോഗങ്ങള്‍ വരെ ഇതു മൂലം ഉണ്ടാകാം എന്നു പറയുന്നു. മറ്റു പല കുട്ടികള്‍ക്കും അതു ചെറിയ രീതിയില്‍ ബാധിക്കും. അലര്‍ജികള്‍ തുടങ്ങിയവ. കുട്ടികളുടെ മാനസികാരോഗ്യത്തെയും സ്വഭാവത്തെയും ഇവ ബാധിക്കുമത്രേ.

ഇതു് പെണ്‍കുട്ടികളെക്കാള്‍ കൂടുതല്‍ ആണ്‍‌കുട്ടികളെയാണു ബാധിക്കുന്നതത്രേ. പെണ്‍കുട്ടികളില്‍ ഉള്ള ഈസ്ട്രോജന്‍ ഹോര്‍മോണ്‍ ഇത്തരം ടോക്സിക് പദാര്‍ത്ഥങ്ങളെ പ്രതിരോധിക്കുമ്പോള്‍ ആണ്‍‌കുട്ടികളിലുള്ള പുരുഷഹോര്‍മോണ്‍ അവയെ സ്വീകരിക്കാന്‍ സഹായിക്കുന്നു.

ഒരു വയസ്സിനു കൊടുക്കുന്ന ചില വാക്സിനേഷനുകളിലാണു് ഏറ്റവും പ്രശ്നമുള്ള പദാര്‍ത്ഥങ്ങളുള്ളതു് എന്നും ഇവര്‍ പറയുന്നു.

ഇതു കേട്ടപ്പോള്‍ ഉണ്ടായ ചില ചിന്തകളും നിരീക്ഷണങ്ങളും. ഇവ വെറും യാദൃച്ഛികമാവാം.

1. എനിക്കറിയാവുന്ന ആണ്‍കുട്ടികളില്‍ ഒരു നല്ല ശതമാനത്തിനും Nuts allergy ഉണ്ടു്. പെണ്‍കുട്ടികളിലും ഇതുണ്ടെങ്കിലും കുറവാണു്. എന്റെ തലമുറയിലെ ഒരാള്‍ക്കും ഈ അലര്‍ജി ഉള്ളതായി ഞാന്‍ കണ്ടിട്ടില്ല. ഇവര്‍ക്കൊക്കെ ഒരു വയസ്സിനു ശേഷമാണു് ഇതു തുടങ്ങിയതെന്നു മാതാപിതാക്കള്‍ പറയുന്നു. Autism തുടങ്ങിയവയും ഒരു വയസ്സിനു ശേഷമാണു തുടങ്ങുന്നതത്രേ.
2. വിശാഖിനു് 9 മാസം പ്രായമുണ്ടായിരുന്നപ്പോള്‍ അവന്റെ അന്നത്തെ ഡോക്ടര്‍ (ഹൈദരാബാദ്) അവനു് MMR കൊടുത്തു. പിന്നീടു കാണിച്ച ഡോക്ടര്‍മാരൊക്കെ അതു തെറ്റായിരുന്നു എന്നു പറഞ്ഞു. (സ്കൂളില്‍ ചേര്‍ക്കാന്‍ നേരം ഒരു വയസ്സിനു ശേഷം രണ്ടു് MMR എടുത്തിരിക്കണം എന്നു പറഞ്ഞതു കൊണ്ടു് ആവശ്യമില്ലാതെ ഒരു ബൂസ്റ്റര്‍ ഷോട്ടും കൂടി എടുക്കേണ്ടി വന്നു.) ഒരു മാസത്തിനുള്ളില്‍ അവനൊരു വലിയ പനി വന്നു. അതു മലേറിയയായിരിക്കും എന്നു പറഞ്ഞു് ഡോക്ടര്‍ അതിന്റെ മരുന്നു കഴിപ്പിച്ചു. (പിന്നെ ചെയ്ത ടെസ്റ്റില്‍ മലേറിയ ഇല്ലെന്നാണു കണ്ടതു്.) ഏതായാലും ആ പനി കൊണ്ടു് ഒന്നില്‍ച്ചില്വാനം കിലോഗ്രാം തൂക്കം കുറഞ്ഞു. അതു് ഇപ്പോഴും അവന്‍ നികത്തിയിട്ടില്ല. ആറര വയസ്സുള്ള അവന്റെ തൂക്കം ഇപ്പോഴും 36 പൌണ്ടാണു് (പതിനാറര കിലോഗ്രാം).
3. ജനിച്ച ആദ്യത്തെ നാളുകളില്‍ നല്ല സ്വഭാവമുണ്ടായിരുന്ന വിഘ്നേശിന്റെ സ്വഭാവത്തില്‍ ഒരു പ്രത്യേക വാക്സിനേഷന്‍ എടുത്തതിന്റെ പിറ്റേ ദിവസം മുതല്‍ ഗണ്യമായ വ്യത്യാസം കണ്ടു തുടങ്ങി. നിസ്സഹകരണം, വഴക്കു്, കരച്ചില്‍ തുടങ്ങിയവ. മറ്റു പല മാതാപിതാക്കളും ഇതിനോടു സദൃശമായ കാര്യങ്ങള്‍ വാക്സിനേഷനുമായി ബന്ധപ്പെടുത്തി പറഞ്ഞിട്ടുണ്ടു്.

ആരോഗ്യവുമായി ബന്ധപ്പെട്ട കാര്യങ്ങളില്‍ എന്റെ അറിവു വളരെ കുറവാണു്. അതിനാലാണു് ഈ പോസ്റ്റിടുന്നതു്. ഇതു വായിക്കുന്ന അറിവുള്ളവര്‍ ദയവായി വസ്തുതകള്‍ പങ്കുവെയ്ക്കണം എന്നു് അപേക്ഷിക്കുന്നു.

പട്ടി കടിച്ചാല്‍ വാക്സിനേഷന്‍ എടുക്കണം എന്ന കാര്യത്തില്‍ സംശയമില്ല. എന്നാല്‍ കുട്ടികളെ ഈ വാക്സിനേഷനുകള്‍ എല്ലാം എടുപ്പിക്കണോ എന്നാണു ചോദ്യം. പല രോഗങ്ങളും വന്നു് പ്രകൃതിയില്‍ നിന്നു തന്നെ പ്രതിരോധശക്തി കിട്ടുന്നതാണു് വാക്സിനേഷന്‍ എടുക്കുന്നതേക്കാള്‍ നല്ലതു് എന്നാണു് വാക്സിനേഷനു് എതിരേ വാദിക്കുന്നവരുടെ അഭിപ്രായം.

ഇതിനോടു ബന്ധപ്പെട്ട ചില വെബ് സൈറ്റുകള്‍:

• Austism Mercury
• Vaccination Libeartion Relay Page

ദേവരാഗം, ഡോ. പണിക്കര്‍, വക്കാരി, സന്തോഷ്, അശോക് കര്‍ത്താ, മാവേലി കേരളം തുടങ്ങി ഈ വിഷയത്തില്‍ അറിവുള്ളവരും റിസര്‍ച്ച് ചെയ്തു കണ്ടുപിടിക്കാന്‍ താത്‌പര്യവുമുള്ള ആളുകളില്‍ നിന്നു പ്രതികരണങ്ങള്‍ പ്രതീക്ഷിക്കുന്നു. ദയവായി ഇതു് പല ചികിത്സാരീതികളെ അങ്ങോട്ടുമിങ്ങോട്ടും ചെളി വാരിയെറിയാനുള്ള വേദിയാക്കരുതു്. ശാസ്ത്രത്തെയും അന്ധമായി വിശ്വസിക്കുന്നതു് അപകടമാ‍ണു് എന്ന അഭിപ്രായക്കാരനാണു ഞാന്‍. എങ്കിലും വികാരങ്ങളെക്കാളും വിശ്വാസങ്ങളെക്കാളും വസ്തുതകളെയാണു കണക്കിലെടുക്കേണ്ടതു് എന്നാണു് എന്റെ അഭിപ്രായം.

വിഘ്നേശിനു് ഒരു വയസ്സാകുമ്പോഴുള്ള വാക്സിനേഷന്‍ അടുത്താഴ്ചയാണു്. അതാണു് തിടുക്കത്തില്‍ ഇങ്ങനെയൊരു പോസ്റ്റ്.

---

Update (January 2015): വിഘ്നേശിനു് അന്നു കൊടുത്തില്ലെങ്കിലും അധികം താമസിയാതെ തന്നെ വാക്സിനേഷൻ കൊടുത്തിരുന്നു. ഓട്ടിസമോ മറ്റു പ്രശ്നങ്ങളോ ഒന്നും ഉണ്ടായില്ല. അവനു് ഇപ്പോൾ എട്ടു വയസ്സ്. മിടുമിടുക്കനായി ഇരിക്കുന്നു.

വാക്സിനേഷൻ എടുക്കണമെന്ന കാര്യത്തിൽ യാതൊരു സംശയവും ഇല്ല. ഡോ. വെയ്ക്ക്ഫീൽഡിന്റെ പഠനം വ്യാജമായിരുന്നു എന്നു തെളിയിക്കപ്പെട്ടു കഴിഞ്ഞു (ഇതു വായിക്കുക.) കൂടെ ഇതും വായിച്ചോളൂ. സെബിന്റെ ഈ പോസ്റ്റും വായിക്കാൻ മറക്കരുതു്.

കുറെക്കാലമായി ബ്ലോഗ്‌പോസ്റ്റുകളെഴുതാനും വായിക്കാനും കമന്റിനു മറുപടി പറയാനും സമയം കിട്ടിയിരുന്നില്ല. ഇതിനിടെ മറുപടി അര്‍ഹിക്കുന്ന ചില കമന്റുകള്‍ പലയിടത്തായി കിട്ടുകയുണ്ടായി. അവയില്‍ സമാനസ്വഭാവമുള്ള ചില കമന്റുകള്‍ക്കു മറുപടിയാണു് ഇവിടെ.

---

എന്റെ അഞ്ജനമെന്നതു ഞാനറിയും എന്ന പോസ്റ്റിനു പി. രാജശേഖര്‍ എഴുതിയ കമന്റ്:

Dear Umesh,

Better late than never…. Yes I was too late see the above discourse on our Traditional Mathematics.

( I was about to contact you … I had a chance to see your Aksharasloka sadas……….it is great….u deserve appreciation!)

I went through Lonappans comment as well as your corrections….

For the completeness I would like to add the following:-

Calculus………It was really invented in Kerala . Madhava who lived in the 14th Cent near Irijalakuda did it.

Except one book( Venuaroham), none of the works of Madhava has been digged out. But he is quoted by suceesors abuntanlly in later works.

The prominent Mathematician NILAKANTA SOMAYAJI ( popularly known as Kelallur Chomathiri) lived from AD 1444 (precisely 1444 June 14) to AD 1545 . He authored the work TANTRA SANGRAHA(1499 AD) & has quoted several verses of Madhava in his various works.
Nilakanta’S sishya was Jyeshtadeva. He wrote the famous book Yuktibhasha( First Malayalam Work in scientific literature). The Lonappans quoted line is from Yukti bhasha. (As you know the Quoted line is in Manipravalam not Sanskrit.. ) Your intrepretation is correct literally. Up to the the Period of Bhaskara, there was only summation of intergers. Madhava, was first in the world to move to the concept of infinitsmal Analysis..

He found that as “n ” tends to infinity sum of natural numbers will tend to n^2/2 & from that he derived the integral of x as x^2/2. Thus when n tends to infinity ” Ekadyakothara Sankalithm” is square of the pada divided by two (pada vargaardham) is correct. Lonappan quoted correctly. But his trasilation to modern terms incorrect as you said. Your intrepretation is correct but you have not considered the “limit’ concept & hence was not able to connect to Pada vargardham.

(From the period of Madhava “pada’ has an additional implied meaning of “variable” also ……..in traditional Maths terminology.)

Yukti Deepika is a work similar to Yuktibhasa by a contemperory of Jyeshta Devan (Between 1500&1600) named Thrikutuveli Sankara Varier.

Puthumana chomathiri was another mathematician who lived more or less in the same period.

Regards
Rajasekhar.P
DOHA/QATAR

നന്ദി. രാജശേഖര്‍ പറഞ്ഞ വസ്തുതകളില്‍ മിക്കതിനോടും യോജിക്കുന്നു.

ലോകശാസ്ത്രചരിത്രത്തില്‍ തൊലി വെളുത്തവരുടെ മാത്രം സംഭാവനകള്‍ പര്‍വ്വതീകരിച്ചും ഭാരതം, ചൈന, ഈജിപ്ത് തുടങ്ങിയ രാജ്യങ്ങളിലെ സംഭാവനകള്‍ പൂര്‍ണ്ണമായി ഒഴിവാക്കിയും ഗ്രീസില്‍ തുടങ്ങി പാശ്ചാത്യലോകത്തു് അവസാനിക്കുന്നതുമാണു ലോകവിജ്ഞാനം എന്നു് വളരെക്കാലമായി പാശ്ചാത്യശാസ്ത്രചരിത്രകാരന്മാരും പ്രചരിപ്പിച്ചിരുന്നു. ഈ ചിന്താഗതിക്കു് ആശാവഹമായ മാറ്റം കണ്ടുവരുന്നുണ്ടു്. ഭാരതത്തിന്റെയും മറ്റു പൌരസ്ത്യരാജ്യങ്ങളുടെയും സംഭാവനകളെ ഇന്നു് ശാസ്ത്രലോകം അംഗീകരിക്കുന്നുണ്ടു്. കാല്‍ക്കുലസിന്റെ കണ്ടുപിടിത്തത്തിനു വഴിയൊരുക്കിയ സിദ്ധാന്തങ്ങള്‍ ഭാരതത്തിലും ഉടലെടുത്തിരുന്നു എന്നു് ഇപ്പോള്‍ മിക്കവരും അംഗീകരിക്കുന്ന കാര്യമാണു്.

ആര്യഭടന്‍, ബ്രഹ്മഗുപ്തന്‍, ഭാസ്കരന്‍ എന്നിവരെപ്പറ്റി മാത്രമേ ഈ അടുത്തകാലം വരെ മറ്റുള്ളവര്‍ അറിഞ്ഞിരുന്നുള്ളൂ. പക്ഷേ ഇപ്പോള്‍ മാധവന്‍, പരമേശ്വരന്‍, നീലകണ്ഠസോമയാജി, പുതുമന സോമയാജി തുടങ്ങിയവരുടെ സംഭാവനകളും ബാഹ്യലോകം അറിയുകയും അംഗീകരിക്കുകയും ചെയ്യുന്നുണ്ടു്. ഈ പുസ്തകങ്ങള്‍ കണ്ടെത്തി തെറ്റില്ലാതെ വ്യക്തമായ വ്യാഖ്യാനത്തോടു കൂടി പ്രസിദ്ധീകരിക്കുകയാണു നാം ചെയ്യേണ്ടതു്.

മാധവന്‍ തുടങ്ങിയവരെപ്പറ്റി ഞാന്‍ ധാരാളം എഴുതിയിട്ടുണ്ടു്. ദയവായി ഭാരതീയഗണിതം എന്ന കാറ്റഗറിയിലെ ലേഖനങ്ങള്‍ വായിച്ചുനോക്കൂ.

ലോനപ്പന്‍ പറഞ്ഞ രണ്ടു കാര്യങ്ങളെയാണു് ഞാന്‍ എതിര്‍ത്തതു്.

1. 3000 വര്‍ഷം മുമ്പു് ചോമാതിരി എന്നൊരാള്‍ കാല്‍ക്കുലസ് ഉണ്ടാക്കി.
2. ഏക ദോകോത്തര സങ്കലിതം പദ വര്‍ഗ്ഗാര്‍‌ദ്ധം എന്നതിന്റെ അര്‍ത്ഥം d/dx of x= 1/2 root(X) എന്നാണു്.

ഇതു രണ്ടും തെറ്റാണെന്നാണു് എന്റെ വിശ്വാസം. കാരണങ്ങള്‍ ആ പോസ്റ്റില്‍ പറഞ്ഞിട്ടുണ്ടു്.

ഏക-ആദി-ഏക-ഉത്തര-സങ്കലിതം ഒന്നു മുതലുള്ള എണ്ണല്‍‌സംഖ്യകളുടെ തുകയല്ലേ? അതിലെങ്ങനെയാണു സീമാസിദ്ധാന്തം ഉപയോഗിച്ചു് സമാകലനം ഉണ്ടാക്കുന്നതു്? സമാകലനത്തിനു് വളരെ ചെറിയ വിഭാഗങ്ങളായി വിഭജിച്ചിട്ടു് അവയുടെ തുക നിര്‍ണ്ണയിക്കണം. ഇതും ഭാരതീയഗണിതജ്ഞര്‍ കണ്ടുപിടിച്ചിരുന്നു. പക്ഷേ ഈ വാക്യത്തില്‍ പറഞ്ഞിരിക്കുന്നതു് അതല്ല. ഈ വാക്യം വ്യാഖ്യാനിച്ചിടത്തു് സമാകലനത്തെപ്പറ്റി പറഞ്ഞിട്ടുണ്ടാവാം.

യുക്തിഭാഷ പണ്ടു വായിച്ചിട്ടുണ്ടു്. എന്റെ കയ്യിലുണ്ടായിരുന്ന പുസ്തകം നഷ്ടപ്പെട്ടു പോയി. കയ്യിലുണ്ടെങ്കില്‍ അതു സ്കാന്‍ ചെയ്തോ ടൈപ്പു ചെയ്തോ പ്രസിദ്ധീകരിക്കാന്‍ ശ്രമിക്കുമോ? രണ്ടു വിധത്തില്‍ ആ പുസ്തകം ശ്രദ്ധേയമാണു്. ഒന്നു്, മലയാളത്തിലെഴുതിയ ഗണിതശാസ്ത്രഗ്രന്ഥം. രണ്ടു്, സാധാരണ ഭാരതീയഗണിതഗ്രന്ഥങ്ങളില്‍ നിന്നു വ്യത്യസ്തമായി തെളിവുകള്‍ സരളമായി പറഞ്ഞിരിക്കുന്നു.

ഞാന്‍ തുടരുന്നു:

ഇവയൊക്കെ കാല്‍ക്കുലസിന്റെ അടിസ്ഥാനതത്ത്വങ്ങള്‍ തന്നെ. എന്നാല്‍ കാല്‍ക്കുലസ് ന്യൂട്ടനു മുമ്പു കണ്ടുപിടിച്ചു എന്നു പറയാനും പറ്റില്ല. നൂറ്റാണ്ടുകള്‍ കൊണ്ടു ഗണിതജ്ഞര്‍ കണ്ടുപിടിച്ച സീമാസിദ്ധാന്തത്തെയും, ചെറിയ ഭാഗങ്ങളാക്കി വിഭജിച്ചു് ഓരോ ഭാഗത്തിന്റെയും വിലയുടെ approximate value കണ്ടുപിടിച്ചു് അവ കൂട്ടി തുക കണ്ടുപിടിക്കുന്ന രീതിയെയും മറ്റും യോജിപ്പിച്ചു് അവകലനത്തിന്റെയും (differentiation) സമാകലനത്തിന്റെയും (integration) സമഗ്രവും സാമാന്യവുമായ നിയമങ്ങള്‍ ഉണ്ടാക്കി എന്നതുകൊണ്ടാണു് കാല്‍ക്കുലസിന്റെ ഉപജ്ഞാതാക്കളായി ന്യൂട്ടനെയും ലൈബ്‌നിറ്റ്സിനെയും കരുതുന്നതു്. ഒരു സുപ്രഭാതത്തില്‍ ഇവര്‍ ഈ തിയറിയൊക്കെ ഉണ്ടാക്കി എന്നല്ല.

ഈപ്പറഞ്ഞതില്‍ ഞാന്‍ ഇപ്പോഴും ഉറച്ചുനില്‍ക്കുന്നു. പക്ഷേ അതിനര്‍ത്ഥം ഞാന്‍ കാല്‍ക്കുലസിന്റെ തിയറിയ്ക്കു് ഭാരതീയര്‍ നല്‍കിയ സംഭാവനകളെ അംഗീകരിക്കുന്നില്ല എന്നല്ല.

ഒരിക്കല്‍ക്കൂടി നന്ദി.

---

എന്റെ എന്റെ ബ്ലോഗും പല തരം അന്ധവിശ്വാസികളും എന്ന പോസ്റ്റിലെ

ബൈബിള്‍ മാത്രമല്ല, വേദങ്ങളും ഖുറാനും മറ്റും ഇങ്ങനെ ആധികാരികഗ്രന്ഥങ്ങളാകാറുണ്ടു്‌. അവ അതാതു കാലത്തെ ഏറ്റവും പ്രഗല്‌ഭരായിരുന്ന മനുഷ്യര്‍ രചിച്ച മഹത്തായ ഗ്രന്ഥങ്ങളാണു്‌ എന്ന വസ്തുത അംഗീകരിക്കാത്ത ഇത്തരം മനുഷ്യരെ നാം “അന്ധവിശ്വാസികള്‍” എന്നു വിളിക്കുന്നു.

എന്ന പരാമര്‍ശനത്തിനു ബി. എന്‍. സുബൈര്‍, അമീര്‍ ഖാന്‍ എന്നിവരില്‍ നിന്നു ലഭിച്ച കമന്റുകള്‍:

• അമീര്‍:
  

  ബൈബിളിനേയും ഖുറാനേയും മറ്റും പറ്റി എഴുതുമ്പോള്‍ അവ കുറഞ്ഞതു് ഒരു് വട്ടമെങ്കിലും വായിച്ചശേഷമായിരുന്നെങ്കില്‍ നന്നായിരുന്നു. എങ്കില്‍ മാത്രമേ ഇത്ര ആധികാരികമായി അതതു് കാലഘട്ടത്തിലെ “മനുഷ്യര്‍” രചിച്ചവയാണവ എന്ന നിരീക്ഷണത്തില്‍ എത്തിച്ചേരാനാവൂ.

• സുബൈര്‍:
  

  ഖുര്‍ ആന്‍ പ്രപഞ്ച സൃഷ്ടാവായ അല്ലാഹുവ്ന്റെ കലാം(വാക്കുകള്‍)ആണ്‌,

  ഖുര്‍ ആന്‍ മനുഷ്യ നിര്‍മ്മിതമാണെങ്കില്‍ അതിലെ ഒരു വാചകത്തിനെങ്കിലും തുല്യമായ മറ്റൊരു വാചകം താങ്കള്‍ക്ക്‌ നിര്‍മ്മിക്കുവാന്‍ കഴിയുമോ? അതിനു വേണ്ടി ഇന്നും, ഇന്നലെയുമായി ലോകത്തുള്ളതും, ഇനി വരുന്നതുമായ എല്ലാ സൗകര്യങ്ങളും, ലോകത്തെ ആരുടെ വേണമെങ്കിലും സേവനവും നിങ്ങള്‍ക്കുപയോഗിക്കാം.

• അമീര്‍ :
  

  മുന്‍വിധിയെന്തിനു് ഉമേഷ്. ഖുറാന്‍ ഒരു വട്ടമെങ്കിലും വായിച്ചതിനു് ശേഷം പോരേ വിധിപ്രസ്താവം? അല്ലെങ്കില്‍ അതും ഒരു അന്ധവിശ്വാസമായിപ്പോവില്ലേ? ഇതു് താങ്കളുടെ തന്നെ നിരീക്ഷണമാണു്.

• സുബൈര്‍:
  

  ചിത്രകാരന്‍ &ഉമേഷ്‌… ഖുര്‍ ആന്‍ അറബി ഭാഷയില്‍ അവതരിച്ച ഗ്രന്ധമാണ്‌, എന്നാല്‍ അത്‌ അറബികളെ മാത്രമല്ല ഫോക്കസ്‌ ചെയ്യുന്നത്‌ എന്ന് താങ്കള്‍ക്ക്‌ ഒറ്റ വായനയില്‍ തന്നെ മനസ്സിലാക്കുവാന്‍ സാധിക്കും,

  എത്ര നിസ്സാരമായാണ്‌ താങ്കള്‍ ഈ വിഷയത്തെ സമീപിച്ചത്‌ എന്നത്‌ എന്നെ അത്ഭുതപ്പെടുത്തുന്നു,
  അക്ഷരാഭ്യാസിയല്ലാതിരുന്ന മുഹമ്മദ്‌ നബി(സ:അ) യില്‍ നിന്നും ഇങ്ങനെയൊരു ഗ്രന്ഥം വിരചിതമായി എന്നത്‌ അക്കാലത്തെ ഏറ്റവും വലിയ ശത്രുക്കള്‍ പോലും ഉന്നയിച്ചിട്ടില്ലാത്ത ഒരാരോപണമാണ്‌..
  ഉമേഷിന്റെ വാക്കുകള്‍ മനസ്സിലാക്കുവാന്‍ പ്രത്യേകിച്ച്‌ ബിദ്ധിമുട്ടുകള്‍ എന്തെങ്കിലും ഉള്ളതായി എനിക്‌ തോന്നുന്നില്ല,
  പിന്നെ താങ്കള്‍ ആ വാദം കൂടുതല്‍ ശക്തമായി ഉന്നയിച്ചതില്‍ നിന്നും ഉമേഷിന്റെ മൗലിക വാദത്തെക്കുറിച്ചും, അന്ധവിശ്വാസസ്ങ്ങളെക്കുറിച്ചും കൂടുതല്‍ വ്യക്തമാകുകയും ചെയ്തു,
  താങ്കള്‍ക്ക്‌ ഈ അറിവ്‌ എവിടെ നിന്നും കിട്ടി എന്നു വെളിവാക്കണമെന്നാവശ്യപ്പെടുന്നതോടൊപ്പം ഞാനെന്റെ വെല്ലുവിളി ആവര്‍ത്തിക്കുകയും ചെയ്യുന്നു…

• അമീര്‍ :
  

  ആദ്യം പറയേണ്ടതായിരുന്നു ഇതു്. ലേഖനം നന്നായിരിക്കുന്നു. പക്ഷേ ഞാനൊരു ക്രിട്ടിക്കല്‍ റീഡര്‍ ആയിപ്പോയി. എന്റെ കുറിപ്പിനു് പക്ഷേ ഞാനൊരു പരാമര്‍ശവും പ്രതീക്ഷിക്കുന്നില്ല.

മുകളില്‍ ഉദ്ധരിച്ചതു രണ്ടു പേരുടെ കമന്റുകളാണെങ്കിലും ഉള്ളടക്കം ഒന്നു തന്നെയാണു്. (അമീര്‍ ഖാനു് ഇംഗ്ലീഷില്‍ ഒരു ബ്ലോഗ് ഉണ്ടു്. നന്നായി എഴുതുന്ന ഒരു ബ്ലോഗ്. സുബൈറിന്റെ മലയാളബ്ലോഗ് തനി മതമൌലികവാദവിഷം മാത്രം.) ഖുര്‍ ആന്‍ തുടങ്ങിയ മതഗ്രന്ഥങ്ങള്‍ മനുഷ്യനെഴുതിയതല്ല, മറിച്ചു് ദൈവം എഴുതിയതാണു്. അതുകൊണ്ടു തന്നെ അവയില്‍ തെറ്റുകളില്ല. ലോകാവസാനം വരെയുള്ള എല്ലാ വിജ്ഞാനവും അപ്-ടു-ഡേറ്റായി അവയിലുണ്ടു്.

അമീര്‍ ഖാനും സുബൈറും ഖുര്‍ ആന്‍-നെപ്പറ്റി മാത്രമേ ഇതു പറയുന്നുള്ളൂ. എന്നു മാത്രമല്ല, ഖുര്‍ ആന്‍ ഒഴികെ ഒരു പുസ്തകവും സമഗ്രമല്ലെന്നും അവര്‍ വാദിക്കുന്നുണ്ടു്. എങ്കിലും മുകളില്‍ ഞാന്‍ മതഗ്രന്ഥങ്ങള്‍ എന്നു ബഹുവചനമായി എഴുതിയതു് ഈ മറുപടി അമീര്‍ ഖാനോടും സുബൈറിനോടും മാത്രമല്ലാത്തതു കൊണ്ടാണു്. ഇതേ വാദഗതികള്‍ ബൈബിളിനെപ്പറ്റിയും വേദങ്ങളെപ്പറ്റിയും കേട്ടിട്ടുണ്ടു്. ദൈവമെഴുതിയതാണു പറയുന്നില്ലെങ്കിലും കുറ്റമറ്റവയാണെന്നുള്ള ലേബല്‍ പല ശാസ്ത്ര-തത്ത്വശാസ്ത്ര-പ്രത്യയശാസ്ത്രഗ്രന്ഥങ്ങളെപ്പറ്റിയും പലരും പറയാറുണ്ടു്. ഞാന്‍ പറയാന്‍ പോകുന്ന പല കാര്യങ്ങളും അവയ്ക്കും കൂടി പ്രസക്തമാണു്.

ഇതു ദൈവത്തിന്റെ അസ്തിത്വത്തെപ്പറ്റിയുള്ള തര്‍ക്കമോ (അവയ്ക്കു് ശ്രീ. കെ. പി. സുകുമാരന്‍ അഞ്ചരക്കണ്ടി, ഡോ. പണിക്കര്‍, അഞ്ചല്‍ക്കാരന്‍ എന്നിവരുടെ ബ്ലോഗുകള്‍ വായിക്കുക) മതഗ്രന്ഥങ്ങളിലെ തെറ്റുകള്‍ നിരത്തുവാനുള്ള ശ്രമമോ, മതഗ്രന്ഥങ്ങള്‍ വായിക്കരുതു് എന്ന ആഹ്വാനമോ അല്ല. മറിച്ചു്, മുകളില്‍ ഉദ്ധരിച്ച ആശയത്തിന്റെ വിമര്‍ശനമാണു്.

ഈ ലോകത്തു് എഴുതുന്ന എല്ലാ ഭാഷകളും മനുഷ്യന്‍ നിര്‍മ്മിച്ചവയാണു്. ദൈവത്തിന്റെ ഭാഷ എന്നു് പല വിശ്വാസപ്രമാണങ്ങള്‍ പിന്തുടരുന്നവര്‍ പല ഭാഷകള്‍ക്കു ലേബലുകള്‍ കൊടുത്തിട്ടുണ്ടു്. ഹിന്ദുക്കള്‍ സംസ്കൃതത്തെയും ക്രിസ്ത്യാനികള്‍ സുറിയാനിയെയും (ബൈബിള്‍ എഴുതിയതു് എബ്രായ, അരമായ, ഗ്രീക്ക് ഭാഷകളിലാണെങ്കിലും സുറിയാനി ദേവഭാഷയായതു മറ്റൊരു ചുറ്റിക്കളി!) മുസ്ലീങ്ങള്‍ അറബിയെയും ഇങ്ങനെ ദേവഭാഷയാക്കിയിട്ടുണ്ടു്. മനുഷ്യനോടു സംവദിക്കാന്‍ ദൈവം ഈ ഭാഷയാണത്രേ ഉപയോഗിക്കുന്നതു്! ഈ ഭാഷയില്‍ അര്‍ത്ഥമറിയാതെയാണെങ്കില്‍ക്കൂടി ഉച്ചരിക്കുന്ന മന്ത്രങ്ങളും വാക്യങ്ങളും മാതൃഭാഷയിലുള്ളവയെക്കാള്‍ പുണ്യം നല്‍കാന്‍ പര്യാപ്തവും ദിവ്യവും ആണെന്നു് അവര്‍ വിശ്വസിക്കുന്നു. വാക്കുകളെക്കാള്‍ പ്രാധാന്യം അതിന്റെ അന്തസ്സത്തയാണെന്നു പ്രഖ്യാപിക്കുന്ന ക്രിസ്തുവചനം പോലും അര്‍ത്ഥം മനസ്സിലാവാത്ത സുറിയാനിയില്‍ വായിച്ചാല്‍ സ്വര്‍ഗ്ഗത്തിനോടു കൂടുതല്‍ അടുക്കാന്‍ സഹായിക്കും എന്ന വിശ്വാസം വളരെ വിചിത്രം തന്നെ!

ഇതിനോടു ബന്ധപ്പെട്ട മറ്റൊരു ആശയവും പ്രാചീനലോകത്തുണ്ടായിരുന്നു. തങ്ങളുടെ നാടാണു ലോകത്തിന്റെ കേന്ദ്രമെന്നു്. ഭൂമി പരന്നതാണെന്നു കരുതിയിരുന്ന ഒരു കാലത്തു് ഭൂമിക്കു് ഒരു കേന്ദ്രപ്രദേശം ഉണ്ടെന്നു കരുതിയതില്‍ തെറ്റില്ല. അതു ദൈവത്തിനു് ഏറ്റവും പ്രിയപ്പെട്ട തങ്ങളുടെ നാടാണെന്നു വരുത്തിത്തീര്‍ക്കേണ്ടതു് തങ്ങളുടെ വിശ്വാസസംഹിത പ്രചരിപ്പിക്കേണ്ട രാഷ്ട്രീയത്തിന്റെ ആവശ്യവുമായിരുന്നു. അതിനാല്‍ ഭൂമി ഉരുണ്ടതാണെന്നറിയാത്ത, അല്ലെങ്കില്‍ മനുഷ്യര്‍ അതു് അറിയരുതെന്നു കരുതുന്ന, ദൈവത്തെക്കൊണ്ടു് അങ്ങനെ പറയിപ്പിച്ചു. ഭൂമി ഉരുണ്ടതാണെന്നുള്ള സത്യം (വിശ്വാസമല്ല, വ്യക്തമായ തെളിവുകള്‍ ഇതിനുണ്ടു്) വ്യക്തമായതിനു ശേഷം ഉണ്ടായ പൂസ്തകങ്ങളില്‍ ഒരു നാടു് ലോകത്തിന്റെ കേന്ദ്രമാണെന്നു പറഞ്ഞിട്ടില്ല. പകരം ഭൂമി പ്രപഞ്ചത്തിന്റെ കേന്ദ്രമാണെന്നു പറഞ്ഞു.

എല്ലാ പുസ്തകങ്ങളും എഴുതിയതു മനുഷ്യനാണു്. ദൈവത്തിന്റെ ആശയങ്ങള്‍ നേരിട്ടോ സ്വപ്നത്തിലോ മാനസികവിഭ്രാന്തിയിലോ കേട്ടിട്ടായിരിക്കാം അവ എഴുതിയതു്. എങ്കിലും എഴുതിയതു മനുഷ്യനാണു്. എഴുതിയ ആള്‍ വളരെ വിജ്ഞാനിയും വിവേകിയുമായ ഒരു ഋഷിയായിരിക്കാം. എങ്കിലും എഴുതിയതു മനുഷ്യനാണു്.

എഴുതിയതു മനുഷ്യനാകുമ്പോള്‍ ഈ പുസ്തകങ്ങള്‍ക്കു ചില പ്രത്യേകതകളും പരിമിതികളുമുണ്ടു്. എഴുതിയ ആളിനറിയാവുന്ന ഭാഷകളില്‍ മാത്രമേ പുസ്തകങ്ങള്‍ എഴുതപ്പെടാന്‍ പറ്റൂ. എഴുതിയ ആളിന്റെ, അല്ലെങ്കില്‍ ആ കാലഘട്ടത്തിന്റെ വിജ്ഞാനത്തിന്റെ പരിധിയില്‍ നിന്നുകൊണ്ടേ എഴുതാന്‍ പറ്റൂ. ഉദാഹരണത്തിനു്, അഷ്ടാംഗഹൃദയത്തില്‍ നാലു തരം രക്തഗ്രൂപ്പുകളെപ്പറ്റിയോ എയിഡ്സ് എന്ന രോഗത്തെപ്പറ്റിയോ ഉള്ള വിവരങ്ങള്‍ ഉണ്ടാകാന്‍ സാദ്ധ്യതയില്ല. ഈ പരിമിതിയ്ക്കുള്ളില്‍ നിന്നുകൊണ്ടാണു് എഴുതിയതു് എന്ന സത്യം പല പുസ്തകങ്ങളും മറച്ചുവെയ്ക്കാന്‍ ശ്രമിക്കുന്നു. അതുകൊണ്ടു് പല കാര്യങ്ങളും എങ്ങനെയും വ്യാഖ്യാനിക്കാവുന്ന മട്ടില്‍ വക്രരീതിയില്‍ പറയുന്നു. പില്‍ക്കാലത്തു് സത്യം കൂടുതല്‍ വ്യക്തമായപ്പോള്‍ അവയുടെ അര്‍ത്ഥം അങ്ങനെയാണെന്നു വ്യാഖ്യാതാക്കള്‍ വ്യാഖ്യാനിക്കുകയും ചെയ്യുന്നു.

ഇതില്‍ പലതും ഇന്നും ശാസ്ത്രത്തിനു വ്യക്തമാകാത്ത കാര്യങ്ങളാണു്. ഉദാഹരണത്തിനു പ്രപഞ്ചം എങ്ങനെ ഉണ്ടായി എന്നതു്. ഇവയെപ്പറ്റി പല മതഗ്രന്ഥങ്ങളിലും കാണുന്ന തിയറികള്‍ ശരിയോ തെറ്റോ എന്നു നമുക്കു പറയാന്‍ സാധിക്കില്ല. പക്ഷേ, ഭൂമിയെ എട്ടു മൂലയിലായി എട്ടു് ആനകള്‍ താങ്ങിനിര്‍ത്തുന്നു എന്ന ഹിന്ദുമതവിശ്വാസവും, ലോകത്തിലെ എല്ലാ സ്പിഷീസിനെയും ദൈവം ആദ്യത്തെ ആറു ദിവസത്തിനുള്ളില്‍ (ഈ ആറു ദിവസം അറുനൂറു കോടി വര്‍ഷമായാലും) സൃഷ്ടിച്ചു എന്നും എല്ലാ സ്പിഷീസിലെയും ഒരു ആണിനെയും പെണ്ണിനെയും ഉള്‍ക്കൊള്ളാന്‍ ബൈബിളില്‍ പറഞ്ഞ ന്നീളവും വീതിയുമുള്ള ഒരു പെട്ടകത്തിനാവും എന്നും ഉള്ള ക്രിസ്ത്യന്‍ വിശ്വാസവും തെറ്റാണെന്നു മനസ്സിലാകാന്‍ ഇന്നു് ഒരാള്‍ക്കു കടുത്ത യുക്തിവാദിയാകേണ്ട കാര്യമില്ല. അന്നന്നത്തെ വിജ്ഞാനമനുസരിച്ചു് അന്നുള്ള പ്രഗല്‍ഭരായ മനുഷ്യര്‍ എഴുതിയ പുസ്തകങ്ങളില്‍ അതിനു ശേഷം വ്യക്തമായ ശാസ്ത്രസത്യങ്ങള്‍ ഉണ്ടെങ്കില്‍ ഒന്നുകില്‍ അതു് എഴുതിയ ആളിന്റെ ഭാവനയായിരിക്കും, അല്ലെങ്കില്‍ തികച്ചും യാദൃച്ഛികമായിരിക്കും.

ഭാഗ്യവശാല്‍, ഭാരതത്തിലെ ശാസ്ത്രജ്ഞര്‍ പുസ്തകങ്ങളില്‍ കാണുന്ന ഫലശ്രുതിയെയും ഐതിഹ്യങ്ങളെയും അവഗണിച്ചു് ഗവേഷണങ്ങള്‍ നടത്തി. സാക്ഷാല്‍ പരമശിവന്‍ ഉടുക്കുകൊട്ടി പാണിനിയ്ക്കു പറഞ്ഞുകൊടുത്തെന്നു പറയപ്പെടുന്ന വ്യാകരണനിയമങ്ങളെ പില്‍ക്കാലത്തു വൈയാകരണന്മാര്‍ തിരുത്തിയെഴുതി. ആര്യഭടന്റെയും വാഗ്‌ഭടന്റെയും മറ്റും സിദ്ധാന്തങ്ങളെ പിന്നീടുള്ളവര്‍ ഉടച്ചുവാര്‍ത്തിട്ടുണ്ടു്. “പുരാണമിത്യേവ ന സാധു സര്‍വ്വം” (പഴയതായതുകൊണ്ടു് എല്ലാം ശരിയല്ല) എന്നു പറഞ്ഞതു കാളിദാസനാണു്. “ഈ സ്തോത്രം നിത്യവും വായിച്ചാല്‍ ഒരിക്കലും മരിക്കില്ല…” എന്നും മറ്റുമുള്ള ഫലശ്രുതികള്‍ അവ എഴുതിയ ആളുകള്‍ തന്നെ വെറുതേ എഴുതിച്ചേര്‍ത്തതാണെന്നു് ആളുകള്‍ക്കറിയാമായിരുന്നു. പഴയ ഗ്രന്ഥങ്ങളില്‍ കാണുന്നതെല്ലാം ശരിയാണെന്നുള്ള കടും‌പിടിത്തം കൂടിയതു് അടുത്ത കാലത്താണു്. മന്ത്രവാദവും ആഭിചാരവും അന്ധവിശ്വാസങ്ങളെ ന്യായീകരിക്കുന്ന വ്യാജശാസ്ത്രവാദങ്ങളും വാസ്തു എന്ന പേരില്‍ നടക്കുന്ന വന്‍ തട്ടിപ്പും ഒക്കെ പ്രചാരത്തിലായിട്ടു് അധികം കാലമായില്ല. ഇന്നത്തെ പ്രസിദ്ധീകരണങ്ങളും ദൃശ്യമാദ്ധ്യമങ്ങളും ഇവയെ പ്രോത്സാഹിപ്പിക്കുന്നുമുണ്ടു്.

ഇതിലെഴുതിയിട്ടുള്ളതു പൂര്‍ണ്ണമായി ശരിയാണെന്നും ഇതിനെ ഒരിക്കലും മാറ്റിയെഴുതരുതെന്നും കാലം എത്ര പുരോഗമിച്ചാലും ഇതില്‍ പറഞ്ഞിരിക്കുന്നതു പോലെയല്ലാതെ ഒന്നും ചെയ്യരുതു് എന്നും ഖുര്‍ ആന്‍ ഉദ്‌ബോധിപ്പിക്കുന്നതാണു് ഇസ്ലാം മതവിശ്വാസികളുടെ യുക്തിയെ പിറകോട്ടു വലിക്കുന്ന നിര്‍ഭാഗ്യകരമായ ഒരു വസ്തുത. മറ്റു മതങ്ങള്‍ തങ്ങളുടെ വിശ്വാസപ്രമാണങ്ങളിലെ നന്മയെ വര്‍ദ്ധിപ്പിക്കാന്‍ ശ്രമിച്ചപ്പോള്‍ നിന്നിടത്തു തന്നെ നില്‍ക്കാനാണു് യാഥാസ്ഥിതിക ഇസ്ലാം വിശ്വാസി താത്പര്യപ്പെടുന്നതു്.

അമീര്‍ ഖാന്റെ കമന്റിനു ശേഷം അറബി അറിയാവുന്ന ഒരു മുസ്ലീം സുഹൃത്തിന്റെ സഹായത്തോടെ ഖുര്‍ ആനിലെ പല ഭാഗങ്ങളും ഞാന്‍ വായിച്ചു. (അതിനു മുമ്പു് ഇംഗ്ലീഷ് പരിഭാഷയിലെ കുറേ ഭാഗം മാത്രമേ വായിച്ചിരുന്നുള്ളൂ.) ശാസ്ത്രവസ്തുതകളെപ്പറ്റി പ്രതിപാദിക്കുന്ന ഭാഗങ്ങളില്‍ ആ കാലത്തിനു ശേഷം ശാസ്ത്രം കണ്ടുപിടിച്ചു എന്നു പറയുന്ന എന്തെങ്കിലും ഉണ്ടോ പരിശോധിക്കുകയായിരുന്നു ഉദ്ദേശ്യം. ഭൂകമ്പങ്ങള്‍, ജ്യോതിശ്ശാസ്ത്രം തുടങ്ങിയ പല കാര്യങ്ങളും. എനിക്കു് ഒന്നും കണ്ടുപിടിക്കാന്‍ കഴിഞ്ഞില്ല. ലോകാവസാനം വരെയുള്ള ശാസ്ത്രം കൃത്യമായി ഖുര്‍ ആനില്‍ ഉണ്ടെന്നു വാദിക്കുന്ന സുഹൃത്തുക്കളിലാരെങ്കിലും ഇതിനുള്ള ഉദാഹരണങ്ങള്‍ ദയവായി ഒരു ബ്ലോഗ്‌പോസ്റ്റായി ഇട്ടിട്ടു് ഇവിടെ ഒരു കമന്റില്‍ അതിലേക്കു് ലിങ്കു കൊടുക്കാമോ? ഈ റമദാന്‍ സമയം ഖുര്‍ ആനെ സംബന്ധിച്ച സത്യങ്ങളെപ്പറ്റി പഠിക്കാനും ബാക്കിയുള്ളവരെ പഠിപ്പിക്കാനും കഴിഞ്ഞാല്‍ അതിലും മഹത്തായ ഒരു കാര്യമുണ്ടോ?

---

മൂന്നു്

എന്റെ രാമായണവും വിമാനവും എന്ന പോസ്റ്റിനു ഹരിദാസ് എഴുതിയ കമന്റ്:

What Umesh is written is same the way the CHRISTAIN machineries doing all over the world to convert the people . Max Muller (Rascal number 1 ) also done in the same thing through his translation of the “Rigveda”. They want to de moralize all the knowledge, culture & civilizations other than Christianity and putting Bible on that space. If they see anything more scientific and modern in others culture, they are considering it is “Mythology”. Wrongly translating the Vedas, Raamaayana, Bagavath Gita Puraanas etc. I think this guy also a Christian machinery getting money and doing the conversion of people.

Just Put the NAME AS “Gurukulam” when I red this I understood this guy doesn’t know the meaning of “What is GURU, What is GURUKULAm & what is GURUTHUWAM”.

Rubbish!!!!

What Haridas wrote is the same way the BLIND HINDU HERITAGE PROPONENTS typically approaching such problems all over the world to mislead people. അതായതു്, കാര്യം എന്താണെന്നു പറയുകയും പറഞ്ഞതിനു ശരിയായ മറുപടി പറയുകയും ചെയ്യാതെ പറഞ്ഞവനെ തെറി വിളിക്കുകയും അവന്‍ ഭാരതീയപൈതൃകത്തില്‍ അഭിമാനിക്കാത്തവനാണെന്നു മുദ്ര കുത്തുകയും ചെയ്യുക. ഇതല്ലാതെ ഇതിലെ പിശകു് എവിടെയാണെന്നു ചൂണ്ടിക്കാട്ടുകയും വാക്കുകള്‍ കൊണ്ടും അസഭ്യം കൊണ്ടും അമ്മാനമാടാതെ വസ്തുതകള്‍ വ്യക്തമാക്കിത്തരുകയും ചെയ്യാന്‍ നിങ്ങള്‍ക്കു കഴിയില്ലേ?

ഭാരതീയവിജ്ഞാനത്തെ de-moralize ചെയ്യാന്‍ ഞാന്‍ ഒരിക്കലും ശ്രമിച്ചിട്ടില്ല; മറിച്ചു് അതിനെപ്പറ്റി കഴിയുന്നത്ര മനസ്സിലാക്കുവാന്‍ ശ്രമിക്കുകയും മനസ്സിലായതു മറ്റുള്ളവര്‍ക്കു പറഞ്ഞുകൊടുക്കാന്‍ ശ്രമിക്കുകയുമാണു്. സംശയമുണ്ടെങ്കില്‍ ഭാരതീയഗണിതത്തെപ്പറ്റിയുള്ള എന്റെ ലേഖനങ്ങള്‍ നോക്കുക.

“രാമായണവും വിമാനവും” എന്ന ലേഖനത്തിലും അതാണു ചെയ്തതു്. വാല്മീകിയുടെ ഭാവനയില്‍ കവിഞ്ഞ എന്തെങ്കിലുമായിരുന്നു വിമാനം എന്നതിനു രാമായണത്തില്‍ തെളിവില്ല എന്നു മാത്രമാണു ഞാന്‍ പറഞ്ഞതു്. അതു തെറ്റാണെങ്കില്‍ എവിടെയാണു് തെളിവു് എന്നു കാണിച്ചുതരുക. ഞാന്‍ അഭിപ്രായം മാറ്റാം.

Wrongly translating the Vedas, Raamaayana, Bagavath Gita Puraanas etc…

ഞാനും ഇതിനു പൂര്‍ണ്ണമായി എതിരാണു സുഹൃത്തേ. Wrongly എന്നതു പുസ്തകത്തില്‍ പറയാത്തതു് എന്ന അര്‍ത്ഥമെടുക്കണം എന്നു മാത്രം.

I think this guy also a Christian machinery getting money and doing the conversion of people…

ഹഹഹ, എന്നെപ്പറ്റിയാണോ ഇതു്? തന്നെ, തന്നെ. ഞാന്‍ ഇവിടെ അമേരിക്കയില്‍ ഒരു സുവിശേഷസെമിനാരിയിലാണു ജോലി ചെയ്യുന്നതു്. സുറിയാനിയിലുള്ള സൂക്തങ്ങള്‍ തപ്പിപ്പിടിച്ചു ബ്ലോഗിലിടുകയാണു പണി. എത്ര ആളുകള്‍ ക്രിസ്ത്യാനികളാകുന്നു എന്നതിനനുസരിച്ചു കാശു കിട്ടുകയും ചെയ്യും. യോഹന്നാന്റെ സുവിശേഷം മൂന്നാം അദ്ധ്യായം പതിനാറാം വാക്യമാണു് എന്റെ ബ്ലോഗിന്റെ ടാഗ്‌ലൈന്‍. മതിയോ?

(പിന്മൊഴി നിര്‍ത്തിയവര്‍ക്കു് ആരോ കൊട്ടക്കണക്കിനു കാശു കൊടുത്തു എന്നു് ഈയിടെ ഒരു മാന്യദേഹം ആരോപണമുന്നയിച്ചിരുന്നു. അതിനെ അപേക്ഷിച്ചു നോക്കുമ്പോള്‍ ഈ ആരോപണം എത്രയോ ഭേദം! ഒന്നുമല്ലെങ്കിലും ദൈവകാര്യത്തിനല്ലേ!)

“ഗുരുക്കന്മാരുടെ കുലം” എന്ന അര്‍ത്ഥത്തിലാണു ഞാന്‍ എന്റെ ബ്ലോഗിനു “ഗുരുകുലം” എന്നു പേരിട്ടതു്. എന്റെ പരിമിതമായ അറിവിന്റെ ഭൂരിഭാഗവും ഗുരുക്കന്മാരില്‍ നിന്നു കിട്ടിയതാണു്. ശരിയാണു്, നിങ്ങള്‍ മനസ്സിലാക്കിയിരിക്കുന്ന രീതിയിലല്ല ഞാന്‍ “ഗുരു” എന്ന വാക്കിന്റെ അര്‍ത്ഥം മനസ്സിലാക്കിയതു്. ഹിന്ദുവല്ലാത്തവരും അചേതനങ്ങളായ വിക്കിപീഡിയ തുടങ്ങിയവയും ശരിയായ ഉച്ചാരണം പറഞ്ഞുതരുന്ന അഞ്ചുവയസ്സുകാരനും എന്റെ ഗുരുക്കളാണു്.

---

പ്രതികരിക്കുന്നവര്‍ ദയവായി ഇതിലെ ഒന്നു്, രണ്ടു്, മൂന്നു് എന്നീ മൂന്നു ഭാഗങ്ങളില്‍ ഏതിന്റെ ഏതു മറുപടിയാണെന്നു വ്യക്തമാക്കുക.